HeuriGym: An Agentic Benchmark for LLM-Crafted Heuristics in Combinatorial Optimization

While Large Language Models (LLMs) have demonstrated significant advancements in reasoning and agent-based problem-solving, current evaluation methodologies fail to adequately assess their capabilities: existing benchmarks either rely on closed-ended questions prone to saturation and memorization, or subjective comparisons that lack consistency and rigor. In this work, we introduce HeuriGym, an agentic framework designed for evaluating heuristic algorithms generated by LLMs for combinatorial optimization problems, characterized by clearly defined objectives and expansive solution spaces. HeuriGym empowers LLMs to propose heuristics, receive evaluative feedback via code execution, and iteratively refine their solutions. We evaluate nine state-of-the-art models on nine problems across domains such as computer systems, logistics, and biology, exposing persistent limitations in tool use, planning, and adaptive reasoning. To quantify performance, we propose the Quality-Yield Index (QYI), a metric that captures both solution pass rate and quality. Even top models like GPT-o4-mini-high and Gemini-2.5-Pro attain QYI scores of only 0.6, well below the expert baseline of 1. Our open-source benchmark aims to guide the development of LLMs toward more effective and realistic problem-solving in scientific and engineering domains.

ScaleRTL: Scaling LLMs with Reasoning Data and Test-Time Compute for Accurate RTL Code Generation

Recent advances in large language models (LLMs) have enabled near-human performance on software coding benchmarks, but their effectiveness in RTL code generation remains limited due to the scarcity of high-quality training data. While prior efforts have fine-tuned LLMs for RTL tasks, they do not fundamentally overcome the data bottleneck and lack support for test-time scaling due to their non-reasoning nature. In this work, we introduce ScaleRTL, the first reasoning LLM for RTL coding that scales up both high-quality reasoning data and test-time compute. Specifically, we curate a diverse set of long chain-of-thought reasoning traces averaging 56K tokens each, resulting in a dataset of 3.5B tokens that captures rich RTL knowledge. Fine-tuning a general-purpose reasoning model on this corpus yields ScaleRTL that is capable of deep RTL reasoning. Subsequently, we further enhance the performance of ScaleRTL through a novel test-time scaling strategy that extends the reasoning process via iteratively reflecting on and self-correcting previous reasoning steps. Experimental results show that ScaleRTL achieves state-of-the-art performance on VerilogEval and RTLLM, outperforming 18 competitive baselines by up to 18.4% on VerilogEval and 12.7% on RTLLM.

JARVIS: A Multi-Agent Code Assistant for High-Quality EDA Script Generation

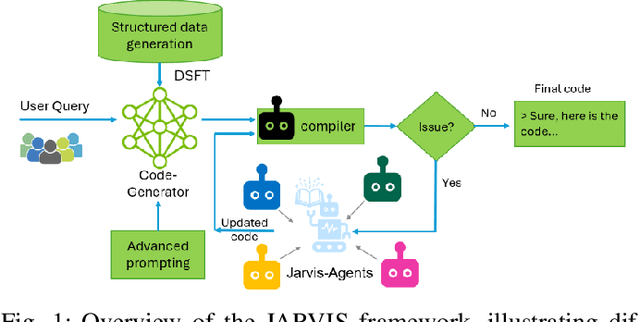
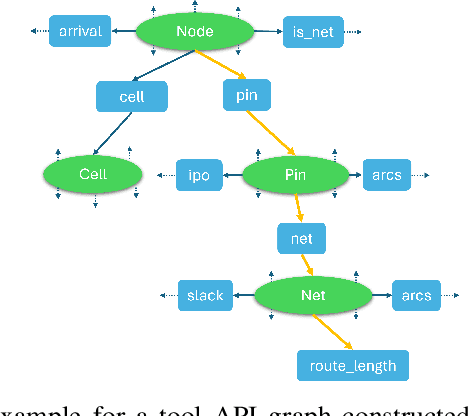
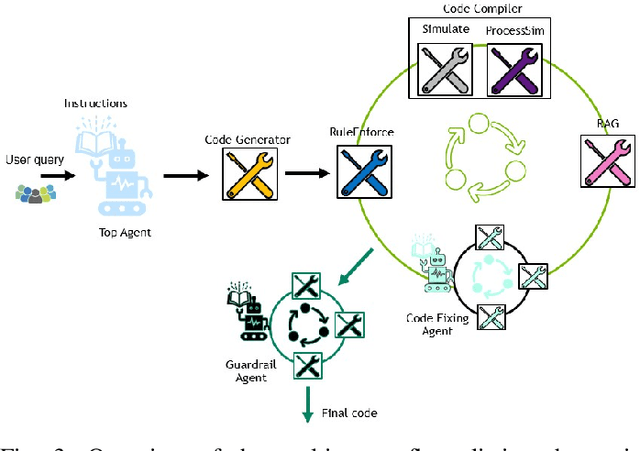
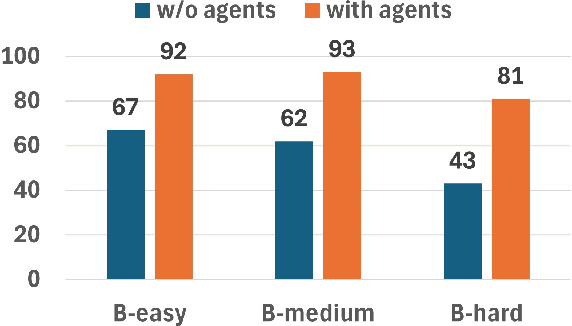
This paper presents JARVIS, a novel multi-agent framework that leverages Large Language Models (LLMs) and domain expertise to generate high-quality scripts for specialized Electronic Design Automation (EDA) tasks. By combining a domain-specific LLM trained with synthetically generated data, a custom compiler for structural verification, rule enforcement, code fixing capabilities, and advanced retrieval mechanisms, our approach achieves significant improvements over state-of-the-art domain-specific models. Our framework addresses the challenges of data scarcity and hallucination errors in LLMs, demonstrating the potential of LLMs in specialized engineering domains. We evaluate our framework on multiple benchmarks and show that it outperforms existing models in terms of accuracy and reliability. Our work sets a new precedent for the application of LLMs in EDA and paves the way for future innovations in this field.

Graph Learning at Scale: Characterizing and Optimizing Pre-Propagation GNNs

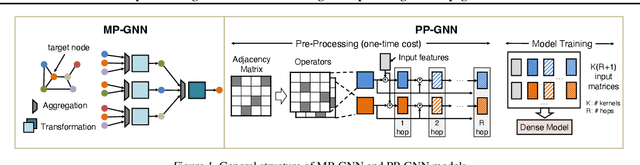
Graph neural networks (GNNs) are widely used for learning node embeddings in graphs, typically adopting a message-passing scheme. This approach, however, leads to the neighbor explosion problem, with exponentially growing computational and memory demands as layers increase. Graph sampling has become the predominant method for scaling GNNs to large graphs, mitigating but not fully solving the issue. Pre-propagation GNNs (PP-GNNs) represent a new class of models that decouple feature propagation from training through pre-processing, addressing neighbor explosion in theory. Yet, their practical advantages and system-level optimizations remain underexplored. This paper provides a comprehensive characterization of PP-GNNs, comparing them with graph-sampling-based methods in training efficiency, scalability, and accuracy. While PP-GNNs achieve comparable accuracy, we identify data loading as the key bottleneck for training efficiency and input expansion as a major scalability challenge. To address these issues, we propose optimized data loading schemes and tailored training methods that improve PP-GNN training throughput by an average of 15$\times$ over the PP-GNN baselines, with speedup of up to 2 orders of magnitude compared to sampling-based GNNs on large graph benchmarks. Our implementation is publicly available at https://github.com/cornell-zhang/preprop-gnn.

ChipAlign: Instruction Alignment in Large Language Models for Chip Design via Geodesic Interpolation

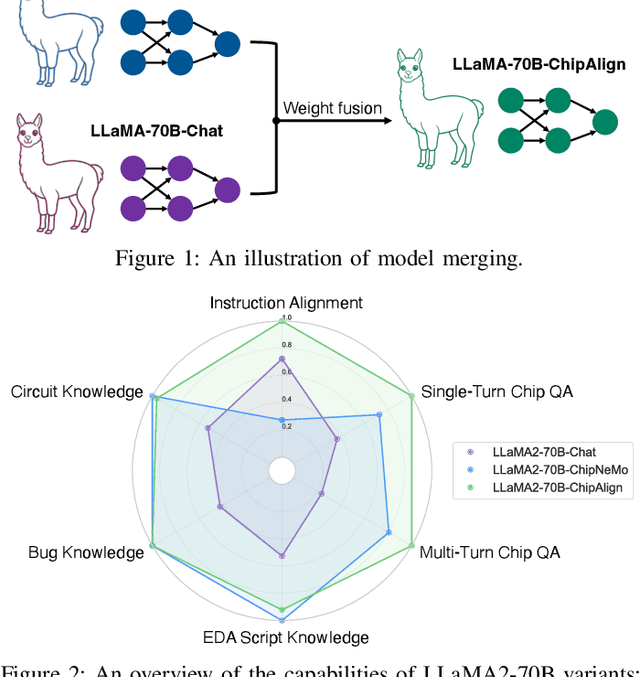
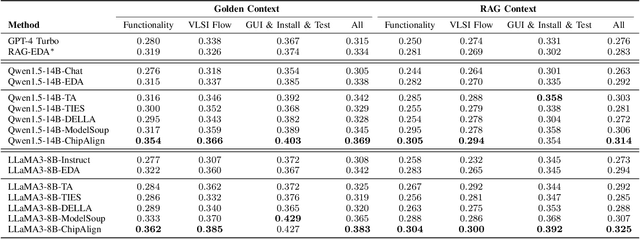
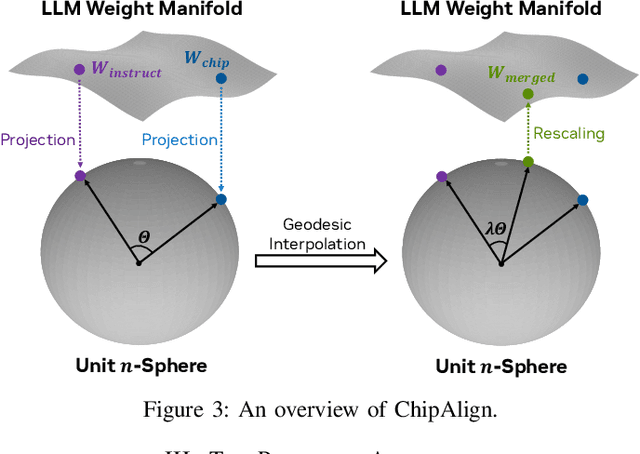
Recent advancements in large language models (LLMs) have expanded their application across various domains, including chip design, where domain-adapted chip models like ChipNeMo have emerged. However, these models often struggle with instruction alignment, a crucial capability for LLMs that involves following explicit human directives. This limitation impedes the practical application of chip LLMs, including serving as assistant chatbots for hardware design engineers. In this work, we introduce ChipAlign, a novel approach that utilizes a training-free model merging strategy, combining the strengths of a general instruction-aligned LLM with a chip-specific LLM. By considering the underlying manifold in the weight space, ChipAlign employs geodesic interpolation to effectively fuse the weights of input LLMs, producing a merged model that inherits strong instruction alignment and chip expertise from the respective instruction and chip LLMs. Our results demonstrate that ChipAlign significantly enhances instruction-following capabilities of existing chip LLMs, achieving up to a 26.6% improvement on the IFEval benchmark, while maintaining comparable expertise in the chip domain. This improvement in instruction alignment also translates to notable gains in instruction-involved QA tasks, delivering performance enhancements of 3.9% on the OpenROAD QA benchmark and 8.25% on production-level chip QA benchmarks, surpassing state-of-the-art baselines.

Less is More: Hop-Wise Graph Attention for Scalable and Generalizable Learning on Circuits

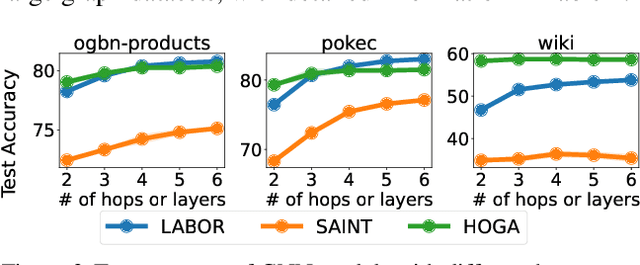
While graph neural networks (GNNs) have gained popularity for learning circuit representations in various electronic design automation (EDA) tasks, they face challenges in scalability when applied to large graphs and exhibit limited generalizability to new designs. These limitations make them less practical for addressing large-scale, complex circuit problems. In this work we propose HOGA, a novel attention-based model for learning circuit representations in a scalable and generalizable manner. HOGA first computes hop-wise features per node prior to model training. Subsequently, the hop-wise features are solely used to produce node representations through a gated self-attention module, which adaptively learns important features among different hops without involving the graph topology. As a result, HOGA is adaptive to various structures across different circuits and can be efficiently trained in a distributed manner. To demonstrate the efficacy of HOGA, we consider two representative EDA tasks: quality of results (QoR) prediction and functional reasoning. Our experimental results indicate that (1) HOGA reduces estimation error over conventional GNNs by 46.76% for predicting QoR after logic synthesis; (2) HOGA improves 10.0% reasoning accuracy over GNNs for identifying functional blocks on unseen gate-level netlists after complex technology mapping; (3) The training time for HOGA almost linearly decreases with an increase in computing resources.

Polynormer: Polynomial-Expressive Graph Transformer in Linear Time

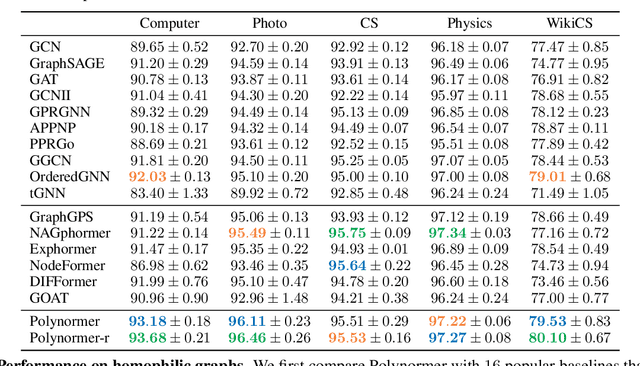
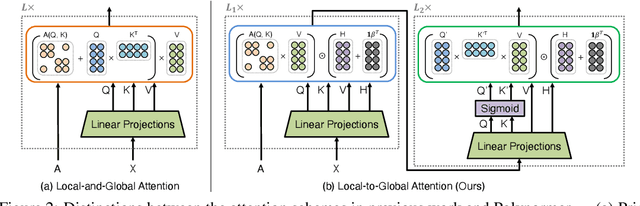
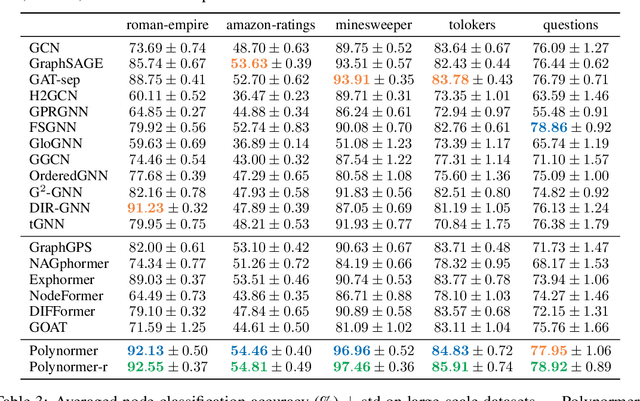
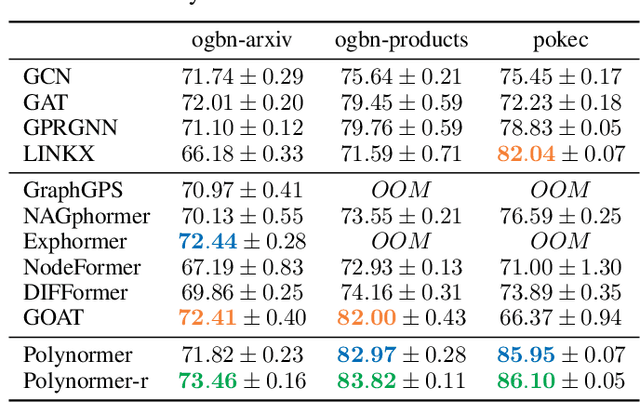
Graph transformers (GTs) have emerged as a promising architecture that is theoretically more expressive than message-passing graph neural networks (GNNs). However, typical GT models have at least quadratic complexity and thus cannot scale to large graphs. While there are several linear GTs recently proposed, they still lag behind GNN counterparts on several popular graph datasets, which poses a critical concern on their practical expressivity. To balance the trade-off between expressivity and scalability of GTs, we propose Polynormer, a polynomial-expressive GT model with linear complexity. Polynormer is built upon a novel base model that learns a high-degree polynomial on input features. To enable the base model permutation equivariant, we integrate it with graph topology and node features separately, resulting in local and global equivariant attention models. Consequently, Polynormer adopts a linear local-to-global attention scheme to learn high-degree equivariant polynomials whose coefficients are controlled by attention scores. Polynormer has been evaluated on $13$ homophilic and heterophilic datasets, including large graphs with millions of nodes. Our extensive experiment results show that Polynormer outperforms state-of-the-art GNN and GT baselines on most datasets, even without the use of nonlinear activation functions.

SAGMAN: Stability Analysis of Graph Neural Networks on the Manifolds

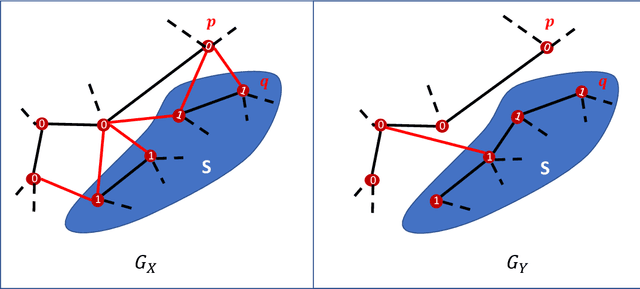
Modern graph neural networks (GNNs) can be sensitive to changes in the input graph structure and node features, potentially resulting in unpredictable behavior and degraded performance. In this work, we introduce a spectral framework known as SAGMAN for examining the stability of GNNs. This framework assesses the distance distortions that arise from the nonlinear mappings of GNNs between the input and output manifolds: when two nearby nodes on the input manifold are mapped (through a GNN model) to two distant ones on the output manifold, it implies a large distance distortion and thus a poor GNN stability. We propose a distance-preserving graph dimension reduction (GDR) approach that utilizes spectral graph embedding and probabilistic graphical models (PGMs) to create low-dimensional input/output graph-based manifolds for meaningful stability analysis. Our empirical evaluations show that SAGMAN effectively assesses the stability of each node when subjected to various edge or feature perturbations, offering a scalable approach for evaluating the stability of GNNs, extending to applications within recommendation systems. Furthermore, we illustrate its utility in downstream tasks, notably in enhancing GNN stability and facilitating adversarial targeted attacks.

GARNET: Reduced-Rank Topology Learning for Robust and Scalable Graph Neural Networks

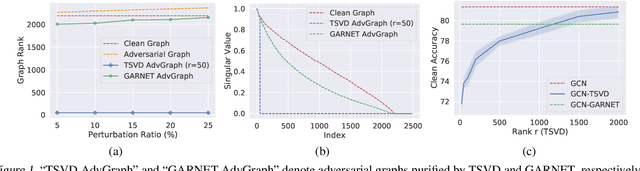
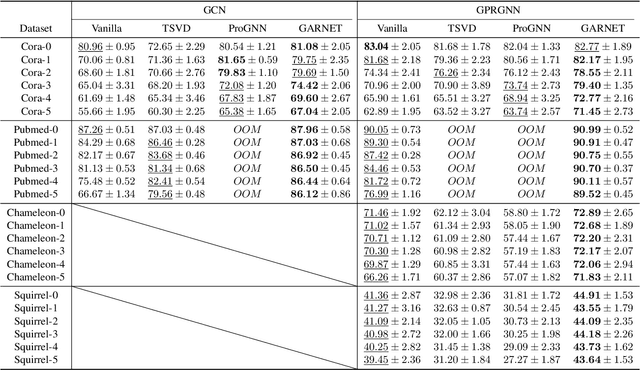
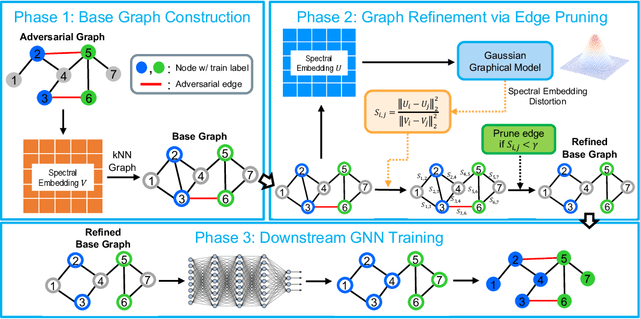
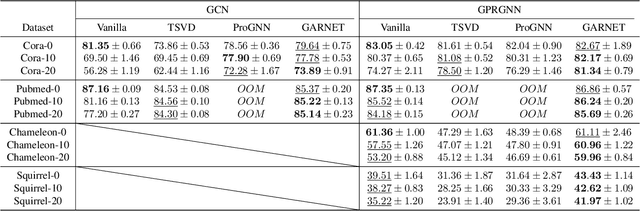
Graph neural networks (GNNs) have been increasingly deployed in various applications that involve learning on non-Euclidean data. However, recent studies show that GNNs are vulnerable to graph adversarial attacks. Although there are several defense methods to improve GNN robustness by eliminating adversarial components, they may also impair the underlying clean graph structure that contributes to GNN training. In addition, few of those defense models can scale to large graphs due to their high computational complexity and memory usage. In this paper, we propose GARNET, a scalable spectral method to boost the adversarial robustness of GNN models. GARNET first leverages weighted spectral embedding to construct a base graph, which is not only resistant to adversarial attacks but also contains critical (clean) graph structure for GNN training. Next, GARNET further refines the base graph by pruning additional uncritical edges based on probabilistic graphical model. GARNET has been evaluated on various datasets, including a large graph with millions of nodes. Our extensive experiment results show that GARNET achieves adversarial accuracy improvement and runtime speedup over state-of-the-art GNN (defense) models by up to 13.27% and 14.7x, respectively.

SPADE: A Spectral Method for Black-Box Adversarial Robustness Evaluation

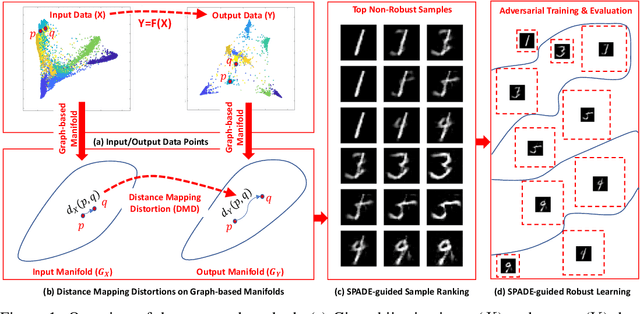
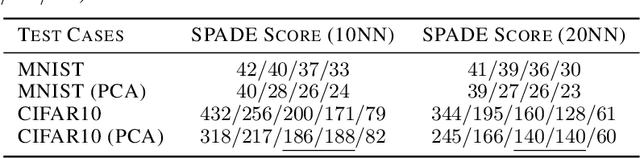
A black-box spectral method is introduced for evaluating the adversarial robustness of a given machine learning (ML) model. Our approach, named SPADE, exploits bijective distance mapping between the input/output graphs constructed for approximating the manifolds corresponding to the input/output data. By leveraging the generalized Courant-Fischer theorem, we propose a SPADE score for evaluating the adversarial robustness of a given model, which is proved to be an upper bound of the best Lipschitz constant under the manifold setting. To reveal the most non-robust data samples highly vulnerable to adversarial attacks, we develop a spectral graph embedding procedure leveraging dominant generalized eigenvectors. This embedding step allows assigning each data sample a robustness score that can be further harnessed for more effective adversarial training. Our experiments show the proposed SPADE method leads to promising empirical results for neural network models adversarially trained with the MNIST and CIFAR-10 data sets.