SHyPar: A Spectral Coarsening Approach to Hypergraph Partitioning

State-of-the-art hypergraph partitioners utilize a multilevel paradigm to construct progressively coarser hypergraphs across multiple layers, guiding cut refinements at each level of the hierarchy. Traditionally, these partitioners employ heuristic methods for coarsening and do not consider the structural features of hypergraphs. In this work, we introduce a multilevel spectral framework, SHyPar, for partitioning large-scale hypergraphs by leveraging hyperedge effective resistances and flow-based community detection techniques. Inspired by the latest theoretical spectral clustering frameworks, such as HyperEF and HyperSF, SHyPar aims to decompose large hypergraphs into multiple subgraphs with few inter-partition hyperedges (cut size). A key component of SHyPar is a flow-based local clustering scheme for hypergraph coarsening, which incorporates a max-flow-based algorithm to produce clusters with substantially improved conductance. Additionally, SHyPar utilizes an effective resistance-based rating function for merging nodes that are strongly connected (coupled). Compared with existing state-of-the-art hypergraph partitioning methods, our extensive experimental results on real-world VLSI designs demonstrate that SHyPar can more effectively partition hypergraphs, achieving state-of-the-art solution quality.

SGM-PINN: Sampling Graphical Models for Faster Training of Physics-Informed Neural Networks

SGM-PINN is a graph-based importance sampling framework to improve the training efficacy of Physics-Informed Neural Networks (PINNs) on parameterized problems. By applying a graph decomposition scheme to an undirected Probabilistic Graphical Model (PGM) built from the training dataset, our method generates node clusters encoding conditional dependence between training samples. Biasing sampling towards more important clusters allows smaller mini-batches and training datasets, improving training speed and accuracy. We additionally fuse an efficient robustness metric with residual losses to determine regions requiring additional sampling. Experiments demonstrate the advantages of the proposed framework, achieving $3\times$ faster convergence compared to prior state-of-the-art sampling methods.

Geodesic Distance Between Graphs: A Spectral Metric for Assessing the Stability of Graph Neural Networks

This paper presents a spectral framework for assessing the generalization and stability of Graph Neural Networks (GNNs) by introducing a Graph Geodesic Distance (GGD) metric. For two different graphs with the same number of nodes, our framework leverages a spectral graph matching procedure to find node correspondence so that the geodesic distance between them can be subsequently computed by solving a generalized eigenvalue problem associated with their Laplacian matrices. For graphs with different sizes, a resistance-based spectral graph coarsening scheme is introduced to reduce the size of the bigger graph while preserving the original spectral properties. We show that the proposed GGD metric can effectively quantify dissimilarities between two graphs by encapsulating their differences in key structural (spectral) properties, such as effective resistances between nodes, cuts, the mixing time of random walks, etc. Through extensive experiments comparing with the state-of-the-art metrics, such as the latest Tree-Mover's Distance (TMD) metric, the proposed GGD metric shows significantly improved performance for stability evaluation of GNNs especially when only partial node features are available.

Researchy Questions: A Dataset of Multi-Perspective, Decompositional Questions for LLM Web Agents

Existing question answering (QA) datasets are no longer challenging to most powerful Large Language Models (LLMs). Traditional QA benchmarks like TriviaQA, NaturalQuestions, ELI5 and HotpotQA mainly study ``known unknowns'' with clear indications of both what information is missing, and how to find it to answer the question. Hence, good performance on these benchmarks provides a false sense of security. A yet unmet need of the NLP community is a bank of non-factoid, multi-perspective questions involving a great deal of unclear information needs, i.e. ``unknown uknowns''. We claim we can find such questions in search engine logs, which is surprising because most question-intent queries are indeed factoid. We present Researchy Questions, a dataset of search engine queries tediously filtered to be non-factoid, ``decompositional'' and multi-perspective. We show that users spend a lot of ``effort'' on these questions in terms of signals like clicks and session length, and that they are also challenging for GPT-4. We also show that ``slow thinking'' answering techniques, like decomposition into sub-questions shows benefit over answering directly. We release $\sim$ 100k Researchy Questions, along with the Clueweb22 URLs that were clicked.

inGRASS: Incremental Graph Spectral Sparsification via Low-Resistance-Diameter Decomposition

This work presents inGRASS, a novel algorithm designed for incremental spectral sparsification of large undirected graphs. The proposed inGRASS algorithm is highly scalable and parallel-friendly, having a nearly-linear time complexity for the setup phase and the ability to update the spectral sparsifier in $O(\log N)$ time for each incremental change made to the original graph with $N$ nodes. A key component in the setup phase of inGRASS is a multilevel resistance embedding framework introduced for efficiently identifying spectrally-critical edges and effectively detecting redundant ones, which is achieved by decomposing the initial sparsifier into many node clusters with bounded effective-resistance diameters leveraging a low-resistance-diameter decomposition (LRD) scheme. The update phase of inGRASS exploits low-dimensional node embedding vectors for efficiently estimating the importance and uniqueness of each newly added edge. As demonstrated through extensive experiments, inGRASS achieves up to over $200 \times$ speedups while retaining comparable solution quality in incremental spectral sparsification of graphs obtained from various datasets, such as circuit simulations, finite element analysis, and social networks.

SAGMAN: Stability Analysis of Graph Neural Networks on the Manifolds

Modern graph neural networks (GNNs) can be sensitive to changes in the input graph structure and node features, potentially resulting in unpredictable behavior and degraded performance. In this work, we introduce a spectral framework known as SAGMAN for examining the stability of GNNs. This framework assesses the distance distortions that arise from the nonlinear mappings of GNNs between the input and output manifolds: when two nearby nodes on the input manifold are mapped (through a GNN model) to two distant ones on the output manifold, it implies a large distance distortion and thus a poor GNN stability. We propose a distance-preserving graph dimension reduction (GDR) approach that utilizes spectral graph embedding and probabilistic graphical models (PGMs) to create low-dimensional input/output graph-based manifolds for meaningful stability analysis. Our empirical evaluations show that SAGMAN effectively assesses the stability of each node when subjected to various edge or feature perturbations, offering a scalable approach for evaluating the stability of GNNs, extending to applications within recommendation systems. Furthermore, we illustrate its utility in downstream tasks, notably in enhancing GNN stability and facilitating adversarial targeted attacks.

A Topology-aware Graph Coarsening Framework for Continual Graph Learning

Continual learning on graphs tackles the problem of training a graph neural network (GNN) where graph data arrive in a streaming fashion and the model tends to forget knowledge from previous tasks when updating with new data. Traditional continual learning strategies such as Experience Replay can be adapted to streaming graphs, however, these methods often face challenges such as inefficiency in preserving graph topology and incapability of capturing the correlation between old and new tasks. To address these challenges, we propose TA$\mathbb{CO}$, a (t)opology-(a)ware graph (co)arsening and (co)ntinual learning framework that stores information from previous tasks as a reduced graph. At each time period, this reduced graph expands by combining with a new graph and aligning shared nodes, and then it undergoes a "zoom out" process by reduction to maintain a stable size. We design a graph coarsening algorithm based on node representation proximities to efficiently reduce a graph and preserve topological information. We empirically demonstrate the learning process on the reduced graph can approximate that of the original graph. Our experiments validate the effectiveness of the proposed framework on three real-world datasets using different backbone GNN models.

SF-SGL: Solver-Free Spectral Graph Learning from Linear Measurements

This work introduces a highly-scalable spectral graph densification framework (SGL) for learning resistor networks with linear measurements, such as node voltages and currents. We show that the proposed graph learning approach is equivalent to solving the classical graphical Lasso problems with Laplacian-like precision matrices. We prove that given $O(\log N)$ pairs of voltage and current measurements, it is possible to recover sparse $N$-node resistor networks that can well preserve the effective resistance distances on the original graph. In addition, the learned graphs also preserve the structural (spectral) properties of the original graph, which can potentially be leveraged in many circuit design and optimization tasks. To achieve more scalable performance, we also introduce a solver-free method (SF-SGL) that exploits multilevel spectral approximation of the graphs and allows for a scalable and flexible decomposition of the entire graph spectrum (to be learned) into multiple different eigenvalue clusters (frequency bands). Such a solver-free approach allows us to more efficiently identify the most spectrally-critical edges for reducing various ranges of spectral embedding distortions. Through extensive experiments for a variety of real-world test cases, we show that the proposed approach is highly scalable for learning sparse resistor networks without sacrificing solution quality. We also introduce a data-driven EDA algorithm for vectorless power/thermal integrity verifications to allow estimating worst-case voltage/temperature (gradient) distributions across the entire chip by leveraging a few voltage/temperature measurements.

HyperEF: Spectral Hypergraph Coarsening by Effective-Resistance Clustering

This paper introduces a scalable algorithmic framework (HyperEF) for spectral coarsening (decomposition) of large-scale hypergraphs by exploiting hyperedge effective resistances. Motivated by the latest theoretical framework for low-resistance-diameter decomposition of simple graphs, HyperEF aims at decomposing large hypergraphs into multiple node clusters with only a few inter-cluster hyperedges. The key component in HyperEF is a nearly-linear time algorithm for estimating hyperedge effective resistances, which allows incorporating the latest diffusion-based non-linear quadratic operators defined on hypergraphs. To achieve good runtime scalability, HyperEF searches within the Krylov subspace (or approximate eigensubspace) for identifying the nearly-optimal vectors for approximating the hyperedge effective resistances. In addition, a node weight propagation scheme for multilevel spectral hypergraph decomposition has been introduced for achieving even greater node coarsening ratios. When compared with state-of-the-art hypergraph partitioning (clustering) methods, extensive experiment results on real-world VLSI designs show that HyperEF can more effectively coarsen (decompose) hypergraphs without losing key structural (spectral) properties of the original hypergraphs, while achieving over $70\times$ runtime speedups over hMetis and $20\times$ speedups over HyperSF.

GARNET: Reduced-Rank Topology Learning for Robust and Scalable Graph Neural Networks

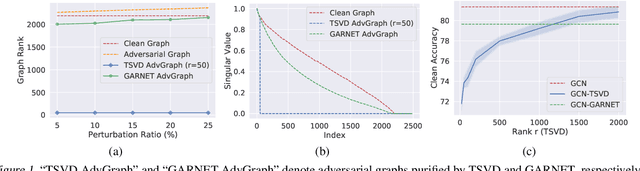
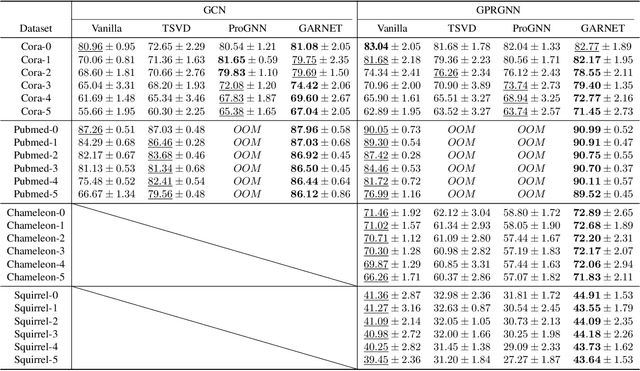
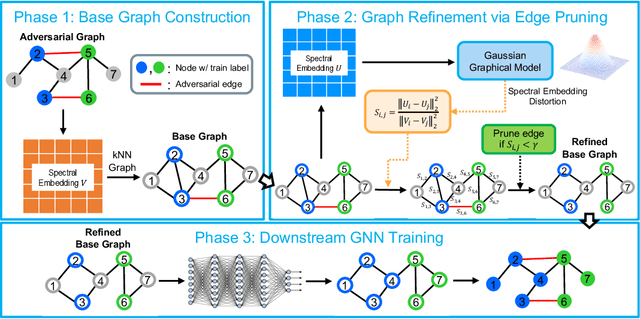
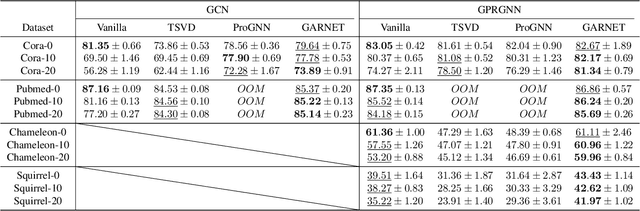
Graph neural networks (GNNs) have been increasingly deployed in various applications that involve learning on non-Euclidean data. However, recent studies show that GNNs are vulnerable to graph adversarial attacks. Although there are several defense methods to improve GNN robustness by eliminating adversarial components, they may also impair the underlying clean graph structure that contributes to GNN training. In addition, few of those defense models can scale to large graphs due to their high computational complexity and memory usage. In this paper, we propose GARNET, a scalable spectral method to boost the adversarial robustness of GNN models. GARNET first leverages weighted spectral embedding to construct a base graph, which is not only resistant to adversarial attacks but also contains critical (clean) graph structure for GNN training. Next, GARNET further refines the base graph by pruning additional uncritical edges based on probabilistic graphical model. GARNET has been evaluated on various datasets, including a large graph with millions of nodes. Our extensive experiment results show that GARNET achieves adversarial accuracy improvement and runtime speedup over state-of-the-art GNN (defense) models by up to 13.27% and 14.7x, respectively.