SHyPar: A Spectral Coarsening Approach to Hypergraph Partitioning

State-of-the-art hypergraph partitioners utilize a multilevel paradigm to construct progressively coarser hypergraphs across multiple layers, guiding cut refinements at each level of the hierarchy. Traditionally, these partitioners employ heuristic methods for coarsening and do not consider the structural features of hypergraphs. In this work, we introduce a multilevel spectral framework, SHyPar, for partitioning large-scale hypergraphs by leveraging hyperedge effective resistances and flow-based community detection techniques. Inspired by the latest theoretical spectral clustering frameworks, such as HyperEF and HyperSF, SHyPar aims to decompose large hypergraphs into multiple subgraphs with few inter-partition hyperedges (cut size). A key component of SHyPar is a flow-based local clustering scheme for hypergraph coarsening, which incorporates a max-flow-based algorithm to produce clusters with substantially improved conductance. Additionally, SHyPar utilizes an effective resistance-based rating function for merging nodes that are strongly connected (coupled). Compared with existing state-of-the-art hypergraph partitioning methods, our extensive experimental results on real-world VLSI designs demonstrate that SHyPar can more effectively partition hypergraphs, achieving state-of-the-art solution quality.

SGM-PINN: Sampling Graphical Models for Faster Training of Physics-Informed Neural Networks

SGM-PINN is a graph-based importance sampling framework to improve the training efficacy of Physics-Informed Neural Networks (PINNs) on parameterized problems. By applying a graph decomposition scheme to an undirected Probabilistic Graphical Model (PGM) built from the training dataset, our method generates node clusters encoding conditional dependence between training samples. Biasing sampling towards more important clusters allows smaller mini-batches and training datasets, improving training speed and accuracy. We additionally fuse an efficient robustness metric with residual losses to determine regions requiring additional sampling. Experiments demonstrate the advantages of the proposed framework, achieving $3\times$ faster convergence compared to prior state-of-the-art sampling methods.

Geodesic Distance Between Graphs: A Spectral Metric for Assessing the Stability of Graph Neural Networks

This paper presents a spectral framework for assessing the generalization and stability of Graph Neural Networks (GNNs) by introducing a Graph Geodesic Distance (GGD) metric. For two different graphs with the same number of nodes, our framework leverages a spectral graph matching procedure to find node correspondence so that the geodesic distance between them can be subsequently computed by solving a generalized eigenvalue problem associated with their Laplacian matrices. For graphs with different sizes, a resistance-based spectral graph coarsening scheme is introduced to reduce the size of the bigger graph while preserving the original spectral properties. We show that the proposed GGD metric can effectively quantify dissimilarities between two graphs by encapsulating their differences in key structural (spectral) properties, such as effective resistances between nodes, cuts, the mixing time of random walks, etc. Through extensive experiments comparing with the state-of-the-art metrics, such as the latest Tree-Mover's Distance (TMD) metric, the proposed GGD metric shows significantly improved performance for stability evaluation of GNNs especially when only partial node features are available.

inGRASS: Incremental Graph Spectral Sparsification via Low-Resistance-Diameter Decomposition

This work presents inGRASS, a novel algorithm designed for incremental spectral sparsification of large undirected graphs. The proposed inGRASS algorithm is highly scalable and parallel-friendly, having a nearly-linear time complexity for the setup phase and the ability to update the spectral sparsifier in $O(\log N)$ time for each incremental change made to the original graph with $N$ nodes. A key component in the setup phase of inGRASS is a multilevel resistance embedding framework introduced for efficiently identifying spectrally-critical edges and effectively detecting redundant ones, which is achieved by decomposing the initial sparsifier into many node clusters with bounded effective-resistance diameters leveraging a low-resistance-diameter decomposition (LRD) scheme. The update phase of inGRASS exploits low-dimensional node embedding vectors for efficiently estimating the importance and uniqueness of each newly added edge. As demonstrated through extensive experiments, inGRASS achieves up to over $200 \times$ speedups while retaining comparable solution quality in incremental spectral sparsification of graphs obtained from various datasets, such as circuit simulations, finite element analysis, and social networks.

SAGMAN: Stability Analysis of Graph Neural Networks on the Manifolds

Modern graph neural networks (GNNs) can be sensitive to changes in the input graph structure and node features, potentially resulting in unpredictable behavior and degraded performance. In this work, we introduce a spectral framework known as SAGMAN for examining the stability of GNNs. This framework assesses the distance distortions that arise from the nonlinear mappings of GNNs between the input and output manifolds: when two nearby nodes on the input manifold are mapped (through a GNN model) to two distant ones on the output manifold, it implies a large distance distortion and thus a poor GNN stability. We propose a distance-preserving graph dimension reduction (GDR) approach that utilizes spectral graph embedding and probabilistic graphical models (PGMs) to create low-dimensional input/output graph-based manifolds for meaningful stability analysis. Our empirical evaluations show that SAGMAN effectively assesses the stability of each node when subjected to various edge or feature perturbations, offering a scalable approach for evaluating the stability of GNNs, extending to applications within recommendation systems. Furthermore, we illustrate its utility in downstream tasks, notably in enhancing GNN stability and facilitating adversarial targeted attacks.

HyperEF: Spectral Hypergraph Coarsening by Effective-Resistance Clustering

This paper introduces a scalable algorithmic framework (HyperEF) for spectral coarsening (decomposition) of large-scale hypergraphs by exploiting hyperedge effective resistances. Motivated by the latest theoretical framework for low-resistance-diameter decomposition of simple graphs, HyperEF aims at decomposing large hypergraphs into multiple node clusters with only a few inter-cluster hyperedges. The key component in HyperEF is a nearly-linear time algorithm for estimating hyperedge effective resistances, which allows incorporating the latest diffusion-based non-linear quadratic operators defined on hypergraphs. To achieve good runtime scalability, HyperEF searches within the Krylov subspace (or approximate eigensubspace) for identifying the nearly-optimal vectors for approximating the hyperedge effective resistances. In addition, a node weight propagation scheme for multilevel spectral hypergraph decomposition has been introduced for achieving even greater node coarsening ratios. When compared with state-of-the-art hypergraph partitioning (clustering) methods, extensive experiment results on real-world VLSI designs show that HyperEF can more effectively coarsen (decompose) hypergraphs without losing key structural (spectral) properties of the original hypergraphs, while achieving over $70\times$ runtime speedups over hMetis and $20\times$ speedups over HyperSF.

HyperSF: Spectral Hypergraph Coarsening via Flow-based Local Clustering

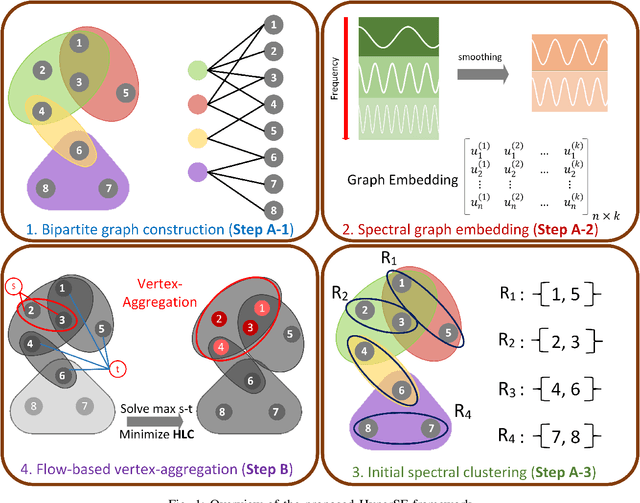
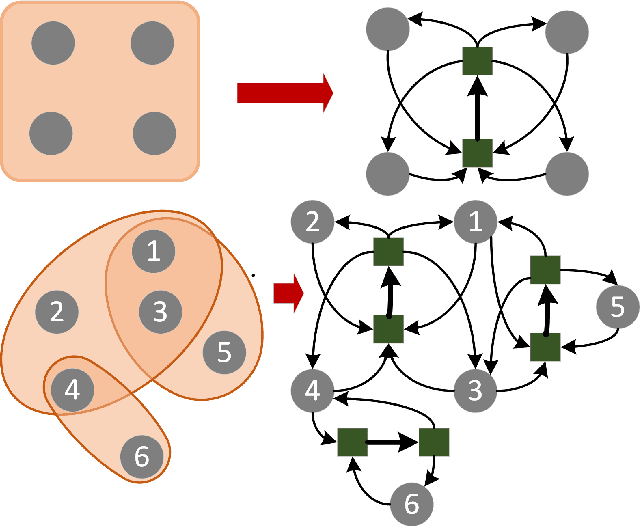
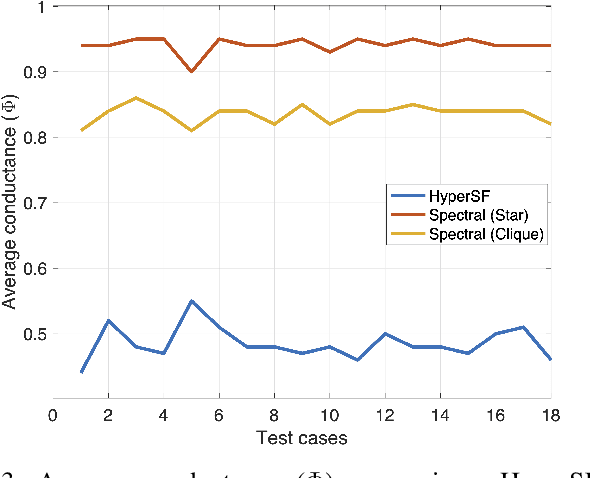
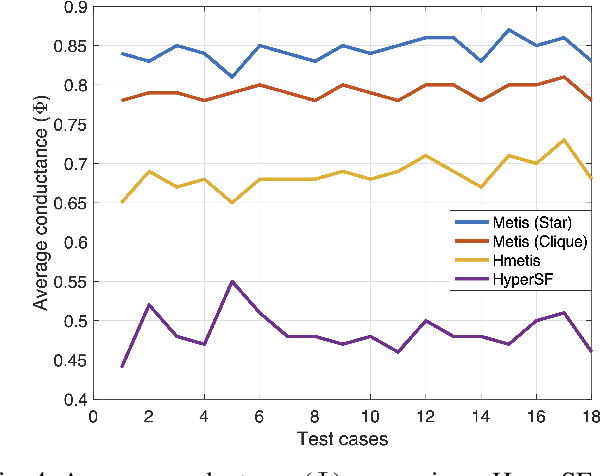
Hypergraphs allow modeling problems with multi-way high-order relationships. However, the computational cost of most existing hypergraph-based algorithms can be heavily dependent upon the input hypergraph sizes. To address the ever-increasing computational challenges, graph coarsening can be potentially applied for preprocessing a given hypergraph by aggressively aggregating its vertices (nodes). However, state-of-the-art hypergraph partitioning (clustering) methods that incorporate heuristic graph coarsening techniques are not optimized for preserving the structural (global) properties of hypergraphs. In this work, we propose an efficient spectral hypergraph coarsening scheme (HyperSF) for well preserving the original spectral (structural) properties of hypergraphs. Our approach leverages a recent strongly-local max-flow-based clustering algorithm for detecting the sets of hypergraph vertices that minimize ratio cut. To further improve the algorithm efficiency, we propose a divide-and-conquer scheme by leveraging spectral clustering of the bipartite graphs corresponding to the original hypergraphs. Our experimental results for a variety of hypergraphs extracted from real-world VLSI design benchmarks show that the proposed hypergraph coarsening algorithm can significantly improve the multi-way conductance of hypergraph clustering as well as runtime efficiency when compared with existing state-of-the-art algorithms.