SGM-PINN: Sampling Graphical Models for Faster Training of Physics-Informed Neural Networks

SGM-PINN is a graph-based importance sampling framework to improve the training efficacy of Physics-Informed Neural Networks (PINNs) on parameterized problems. By applying a graph decomposition scheme to an undirected Probabilistic Graphical Model (PGM) built from the training dataset, our method generates node clusters encoding conditional dependence between training samples. Biasing sampling towards more important clusters allows smaller mini-batches and training datasets, improving training speed and accuracy. We additionally fuse an efficient robustness metric with residual losses to determine regions requiring additional sampling. Experiments demonstrate the advantages of the proposed framework, achieving $3\times$ faster convergence compared to prior state-of-the-art sampling methods.

RITA: A Real-time Interactive Talking Avatars Framework

RITA presents a high-quality real-time interactive framework built upon generative models, designed with practical applications in mind. Our framework enables the transformation of user-uploaded photos into digital avatars that can engage in real-time dialogue interactions. By leveraging the latest advancements in generative modeling, we have developed a versatile platform that not only enhances the user experience through dynamic conversational avatars but also opens new avenues for applications in virtual reality, online education, and interactive gaming. This work showcases the potential of integrating computer vision and natural language processing technologies to create immersive and interactive digital personas, pushing the boundaries of how we interact with digital content.

SAGMAN: Stability Analysis of Graph Neural Networks on the Manifolds

Modern graph neural networks (GNNs) can be sensitive to changes in the input graph structure and node features, potentially resulting in unpredictable behavior and degraded performance. In this work, we introduce a spectral framework known as SAGMAN for examining the stability of GNNs. This framework assesses the distance distortions that arise from the nonlinear mappings of GNNs between the input and output manifolds: when two nearby nodes on the input manifold are mapped (through a GNN model) to two distant ones on the output manifold, it implies a large distance distortion and thus a poor GNN stability. We propose a distance-preserving graph dimension reduction (GDR) approach that utilizes spectral graph embedding and probabilistic graphical models (PGMs) to create low-dimensional input/output graph-based manifolds for meaningful stability analysis. Our empirical evaluations show that SAGMAN effectively assesses the stability of each node when subjected to various edge or feature perturbations, offering a scalable approach for evaluating the stability of GNNs, extending to applications within recommendation systems. Furthermore, we illustrate its utility in downstream tasks, notably in enhancing GNN stability and facilitating adversarial targeted attacks.

SPADE: A Spectral Method for Black-Box Adversarial Robustness Evaluation

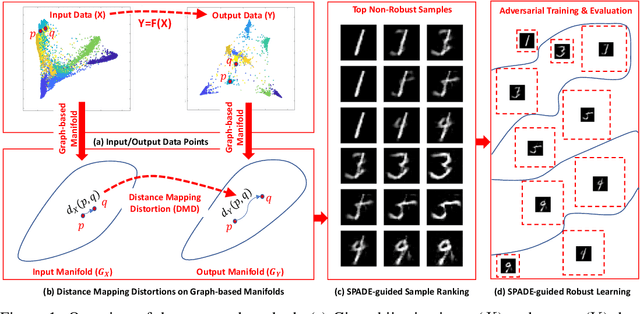
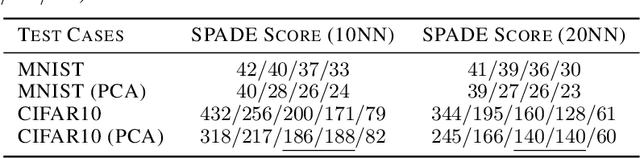
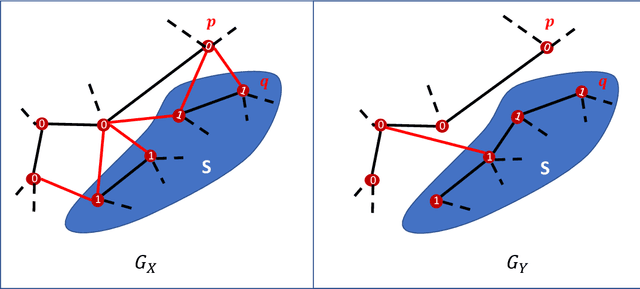
A black-box spectral method is introduced for evaluating the adversarial robustness of a given machine learning (ML) model. Our approach, named SPADE, exploits bijective distance mapping between the input/output graphs constructed for approximating the manifolds corresponding to the input/output data. By leveraging the generalized Courant-Fischer theorem, we propose a SPADE score for evaluating the adversarial robustness of a given model, which is proved to be an upper bound of the best Lipschitz constant under the manifold setting. To reveal the most non-robust data samples highly vulnerable to adversarial attacks, we develop a spectral graph embedding procedure leveraging dominant generalized eigenvectors. This embedding step allows assigning each data sample a robustness score that can be further harnessed for more effective adversarial training. Our experiments show the proposed SPADE method leads to promising empirical results for neural network models adversarially trained with the MNIST and CIFAR-10 data sets.