Enhancing Character-Level Understanding in LLMs through Token Internal Structure Learning

Tokenization techniques such as Byte-Pair Encoding (BPE) and Byte-Level BPE (BBPE) have significantly improved the computational efficiency and vocabulary representation stability of large language models (LLMs) by segmenting text into tokens. However, this segmentation often obscures the internal character structures and sequences within tokens, preventing models from fully learning these intricate details during training. Consequently, LLMs struggle to comprehend the character compositions and positional relationships within tokens, especially when fine-tuned on downstream tasks with limited data. In this paper, we introduce Token Internal Position Awareness (TIPA), a novel approach that enhances LLMs' understanding of internal token structures by training them on reverse character prediction tasks using the tokenizer's own vocabulary. This method enables models to effectively learn and generalize character positions and internal structures. Experimental results demonstrate that LLMs trained with TIPA outperform baseline models in predicting character positions at the token level. Furthermore, when applied to the downstream task of Chinese Spelling Correction (CSC), TIPA not only accelerates model convergence but also significantly improves task performance.

Combining Relevance and Magnitude for Resource-Aware DNN Pruning

Pruning neural networks, i.e., removing some of their parameters whilst retaining their accuracy, is one of the main ways to reduce the latency of a machine learning pipeline, especially in resource- and/or bandwidth-constrained scenarios. In this context, the pruning technique, i.e., how to choose the parameters to remove, is critical to the system performance. In this paper, we propose a novel pruning approach, called FlexRel and predicated upon combining training-time and inference-time information, namely, parameter magnitude and relevance, in order to improve the resulting accuracy whilst saving both computational resources and bandwidth. Our performance evaluation shows that FlexRel is able to achieve higher pruning factors, saving over 35% bandwidth for typical accuracy targets.

SF-SGL: Solver-Free Spectral Graph Learning from Linear Measurements

This work introduces a highly-scalable spectral graph densification framework (SGL) for learning resistor networks with linear measurements, such as node voltages and currents. We show that the proposed graph learning approach is equivalent to solving the classical graphical Lasso problems with Laplacian-like precision matrices. We prove that given $O(\log N)$ pairs of voltage and current measurements, it is possible to recover sparse $N$-node resistor networks that can well preserve the effective resistance distances on the original graph. In addition, the learned graphs also preserve the structural (spectral) properties of the original graph, which can potentially be leveraged in many circuit design and optimization tasks. To achieve more scalable performance, we also introduce a solver-free method (SF-SGL) that exploits multilevel spectral approximation of the graphs and allows for a scalable and flexible decomposition of the entire graph spectrum (to be learned) into multiple different eigenvalue clusters (frequency bands). Such a solver-free approach allows us to more efficiently identify the most spectrally-critical edges for reducing various ranges of spectral embedding distortions. Through extensive experiments for a variety of real-world test cases, we show that the proposed approach is highly scalable for learning sparse resistor networks without sacrificing solution quality. We also introduce a data-driven EDA algorithm for vectorless power/thermal integrity verifications to allow estimating worst-case voltage/temperature (gradient) distributions across the entire chip by leveraging a few voltage/temperature measurements.

HyperSF: Spectral Hypergraph Coarsening via Flow-based Local Clustering

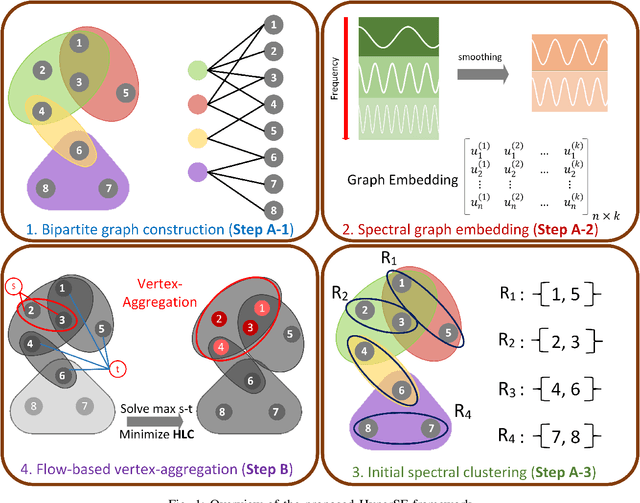
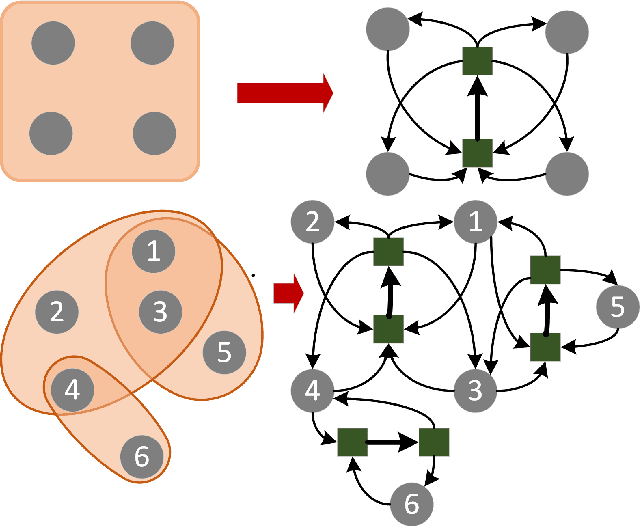
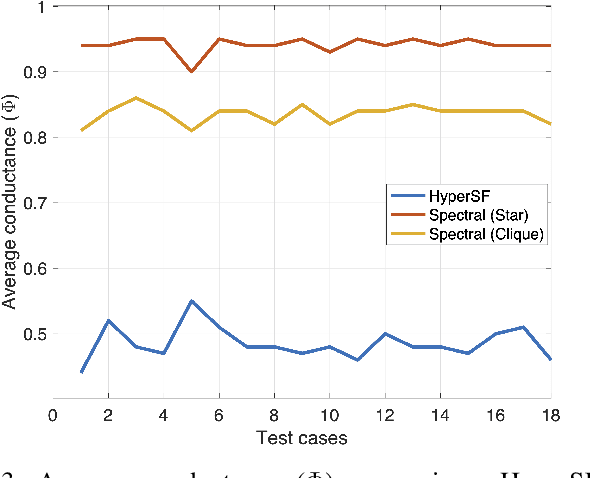
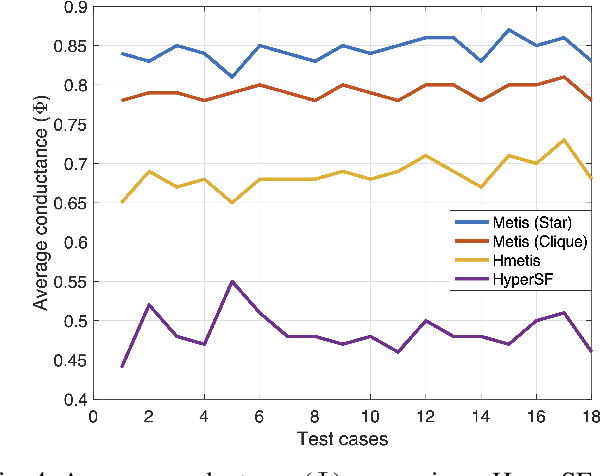
Hypergraphs allow modeling problems with multi-way high-order relationships. However, the computational cost of most existing hypergraph-based algorithms can be heavily dependent upon the input hypergraph sizes. To address the ever-increasing computational challenges, graph coarsening can be potentially applied for preprocessing a given hypergraph by aggressively aggregating its vertices (nodes). However, state-of-the-art hypergraph partitioning (clustering) methods that incorporate heuristic graph coarsening techniques are not optimized for preserving the structural (global) properties of hypergraphs. In this work, we propose an efficient spectral hypergraph coarsening scheme (HyperSF) for well preserving the original spectral (structural) properties of hypergraphs. Our approach leverages a recent strongly-local max-flow-based clustering algorithm for detecting the sets of hypergraph vertices that minimize ratio cut. To further improve the algorithm efficiency, we propose a divide-and-conquer scheme by leveraging spectral clustering of the bipartite graphs corresponding to the original hypergraphs. Our experimental results for a variety of hypergraphs extracted from real-world VLSI design benchmarks show that the proposed hypergraph coarsening algorithm can significantly improve the multi-way conductance of hypergraph clustering as well as runtime efficiency when compared with existing state-of-the-art algorithms.

SPADE: A Spectral Method for Black-Box Adversarial Robustness Evaluation

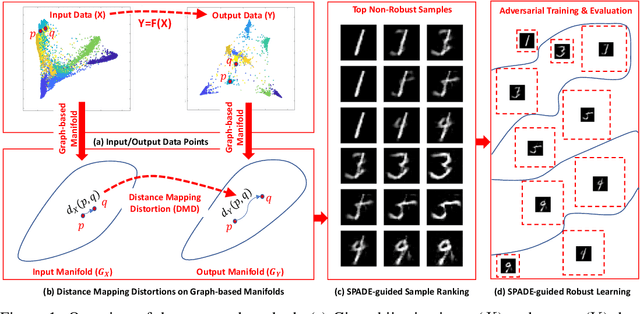
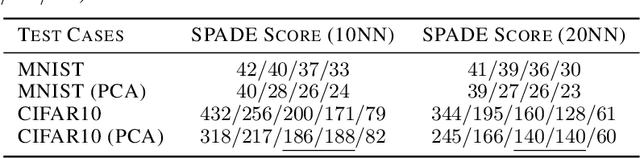
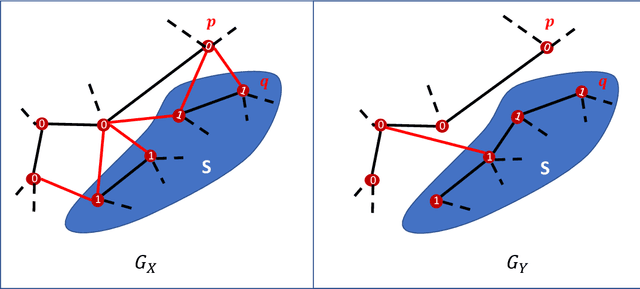
A black-box spectral method is introduced for evaluating the adversarial robustness of a given machine learning (ML) model. Our approach, named SPADE, exploits bijective distance mapping between the input/output graphs constructed for approximating the manifolds corresponding to the input/output data. By leveraging the generalized Courant-Fischer theorem, we propose a SPADE score for evaluating the adversarial robustness of a given model, which is proved to be an upper bound of the best Lipschitz constant under the manifold setting. To reveal the most non-robust data samples highly vulnerable to adversarial attacks, we develop a spectral graph embedding procedure leveraging dominant generalized eigenvectors. This embedding step allows assigning each data sample a robustness score that can be further harnessed for more effective adversarial training. Our experiments show the proposed SPADE method leads to promising empirical results for neural network models adversarially trained with the MNIST and CIFAR-10 data sets.

SF-GRASS: Solver-Free Graph Spectral Sparsification

Recent spectral graph sparsification techniques have shown promising performance in accelerating many numerical and graph algorithms, such as iterative methods for solving large sparse matrices, spectral partitioning of undirected graphs, vectorless verification of power/thermal grids, representation learning of large graphs, etc. However, prior spectral graph sparsification methods rely on fast Laplacian matrix solvers that are usually challenging to implement in practice. This work, for the first time, introduces a solver-free approach (SF-GRASS) for spectral graph sparsification by leveraging emerging spectral graph coarsening and graph signal processing (GSP) techniques. We introduce a local spectral embedding scheme for efficiently identifying spectrally-critical edges that are key to preserving graph spectral properties, such as the first few Laplacian eigenvalues and eigenvectors. Since the key kernel functions in SF-GRASS can be efficiently implemented using sparse-matrix-vector-multiplications (SpMVs), the proposed spectral approach is simple to implement and inherently parallel friendly. Our extensive experimental results show that the proposed method can produce a hierarchy of high-quality spectral sparsifiers in nearly-linear time for a variety of real-world, large-scale graphs and circuit networks when compared with the prior state-of-the-art spectral method.

GRASPEL: Graph Spectral Learning at Scale

Learning meaningful graphs from data plays important roles in many data mining and machine learning tasks, such as data representation and analysis, dimension reduction, data clustering, and visualization, etc. In this work, for the first time, we present a highly-scalable spectral approach (GRASPEL) for learning large graphs from data. By limiting the precision matrix to be a graph Laplacian, our approach aims to estimate ultra-sparse (tree-like) weighted undirected graphs and shows a clear connection with the prior graphical Lasso method. By interleaving the latest high-performance nearly-linear time spectral methods for graph sparsification, coarsening and embedding, ultra-sparse yet spectrally-robust graphs can be learned by identifying and including the most spectrally-critical edges into the graph. Compared with prior state-of-the-art graph learning approaches, GRASPEL is more scalable and allows substantially improving computing efficiency and solution quality of a variety of data mining and machine learning applications, such as spectral clustering (SC), and t-Distributed Stochastic Neighbor Embedding (t-SNE). {For example, when comparing with graphs constructed using existing methods, GRASPEL achieved the best spectral clustering efficiency and accuracy.

GraphZoom: A multi-level spectral approach for accurate and scalable graph embedding

Graph embedding techniques have been increasingly deployed in a multitude of different applications that involve learning on non-Euclidean data. However, existing graph embedding models either fail to incorporate node attribute information during training or suffer from node attribute noise, which compromises the accuracy. Moreover, very few of them scale to large graphs due to their high computational complexity and memory usage. In this paper we propose GraphZoom, a multi-level framework for improving both accuracy and scalability of unsupervised graph embedding algorithms. GraphZoom first performs graph fusion to generate a new graph that effectively encodes the topology of the original graph and the node attribute information. This fused graph is then repeatedly coarsened into a much smaller graph by merging nodes with high spectral similarities. GraphZoom allows any existing embedding methods to be applied to the coarsened graph, before it progressively refine the embeddings obtained at the coarsest level to increasingly finer graphs. We have evaluated our approach on a number of popular graph datasets for both transductive and inductive tasks. Our experiments show that GraphZoom increases the classification accuracy and significantly reduces the run time compared to state-of-the-art unsupervised embedding methods.