Sampling Foundational Transformer: A Theoretical Perspective
Paper and Code
Aug 11, 2024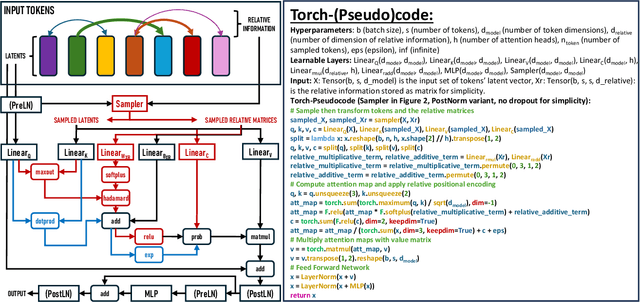
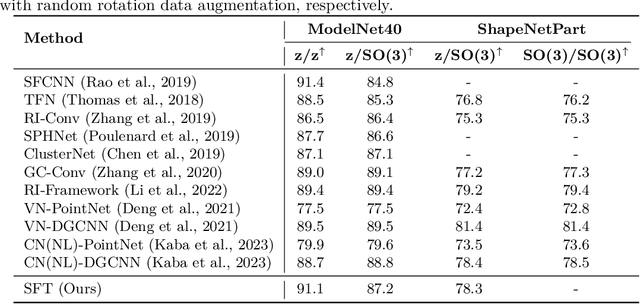
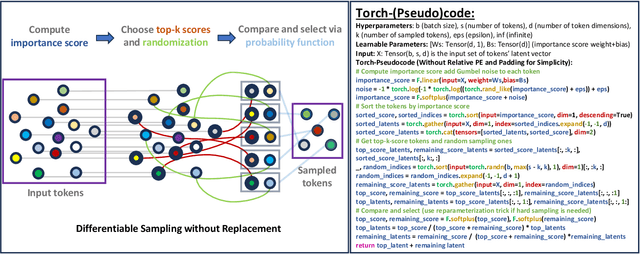
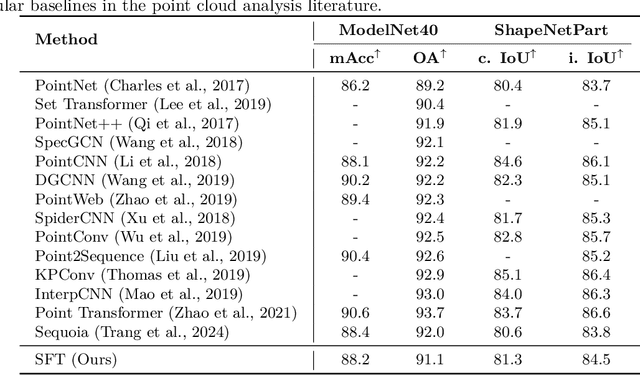
The versatility of self-attention mechanism earned transformers great success in almost all data modalities, with limitations on the quadratic complexity and difficulty of training. To apply transformers across different data modalities, practitioners have to make specific clever data-modality-dependent constructions. In this paper, we propose Sampling Foundational Transformer (SFT) that can work on multiple data modalities (e.g., point cloud, graph, and sequence) and constraints (e.g., rotational-invariant). The existence of such model is important as contemporary foundational modeling requires operability on multiple data sources. For efficiency on large number of tokens, our model relies on our context aware sampling-without-replacement mechanism for both linear asymptotic computational complexity and real inference time gain. For efficiency, we rely on our newly discovered pseudoconvex formulation of transformer layer to increase model's convergence rate. As a model working on multiple data modalities, SFT has achieved competitive results on many benchmarks, while being faster in inference, compared to other very specialized models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge