Learning to Solve Multiresolution Matrix Factorization by Manifold Optimization and Evolutionary Metaheuristics

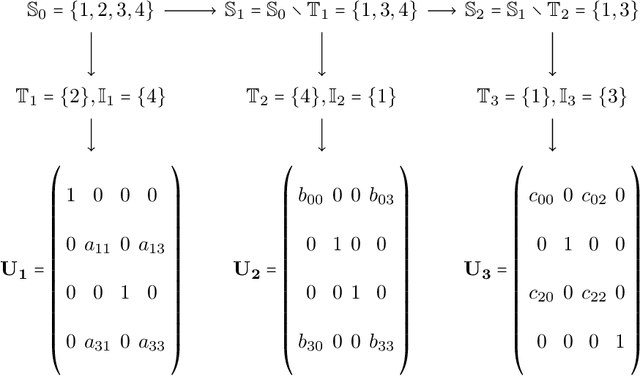
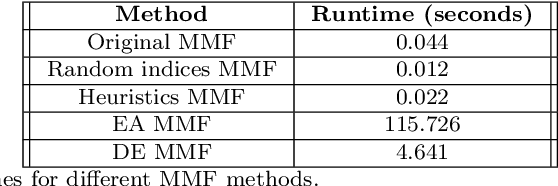
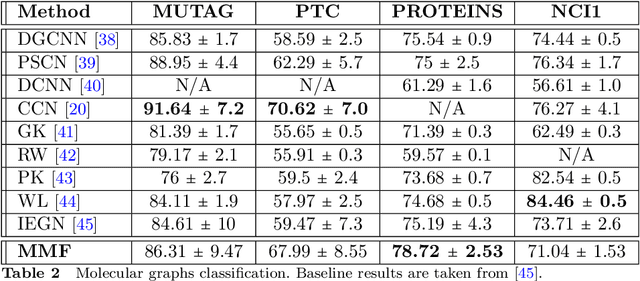
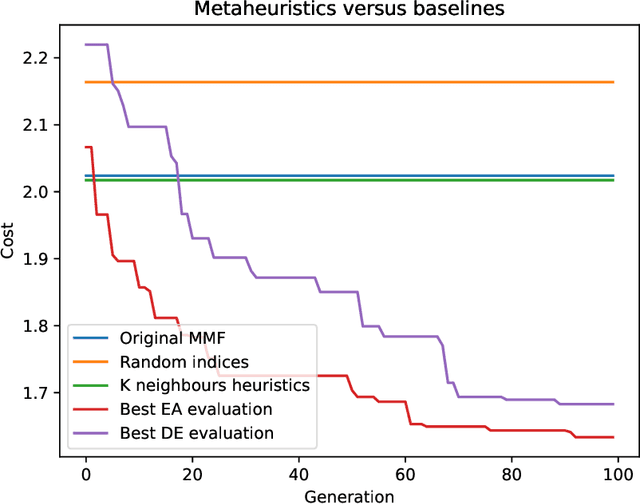
Multiresolution Matrix Factorization (MMF) is unusual amongst fast matrix factorization algorithms in that it does not make a low rank assumption. This makes MMF especially well suited to modeling certain types of graphs with complex multiscale or hierarchical strucutre. While MMF promises to yields a useful wavelet basis, finding the factorization itself is hard, and existing greedy methods tend to be brittle. In this paper, we propose a ``learnable'' version of MMF that carfully optimizes the factorization using metaheuristics, specifically evolutionary algorithms and directed evolution, along with Stiefel manifold optimization through backpropagating errors. We show that the resulting wavelet basis far outperforms prior MMF algorithms and gives comparable performance on standard learning tasks on graphs. Furthermore, we construct the wavelet neural networks (WNNs) learning graphs on the spectral domain with the wavelet basis produced by our MMF learning algorithm. Our wavelet networks are competitive against other state-of-the-art methods in molecular graphs classification and node classification on citation graphs. We release our implementation at https://github.com/HySonLab/LearnMMF

Steerable Transformers

In this work we introduce Steerable Transformers, an extension of the Vision Transformer mechanism that maintains equivariance to the special Euclidean group $\mathrm{SE}(d)$. We propose an equivariant attention mechanism that operates on features extracted by steerable convolutions. Operating in Fourier space, our network utilizes Fourier space non-linearities. Our experiments in both two and three dimensions show that adding a steerable transformer encoder layer to a steerable convolution network enhances performance.

Sign Rank Limitations for Attention-Based Graph Decoders

Inner product-based decoders are among the most influential frameworks used to extract meaningful data from latent embeddings. However, such decoders have shown limitations in representation capacity in numerous works within the literature, which have been particularly notable in graph reconstruction problems. In this paper, we provide the first theoretical elucidation of this pervasive phenomenon in graph data, and suggest straightforward modifications to circumvent this issue without deviating from the inner product framework.

Transformers are efficient hierarchical chemical graph learners

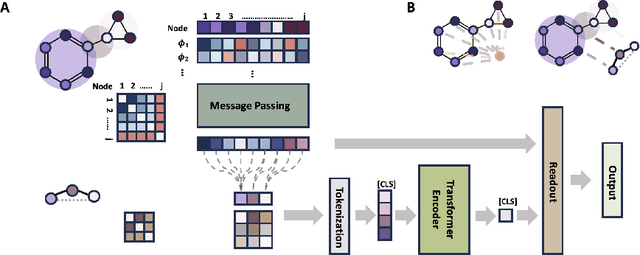
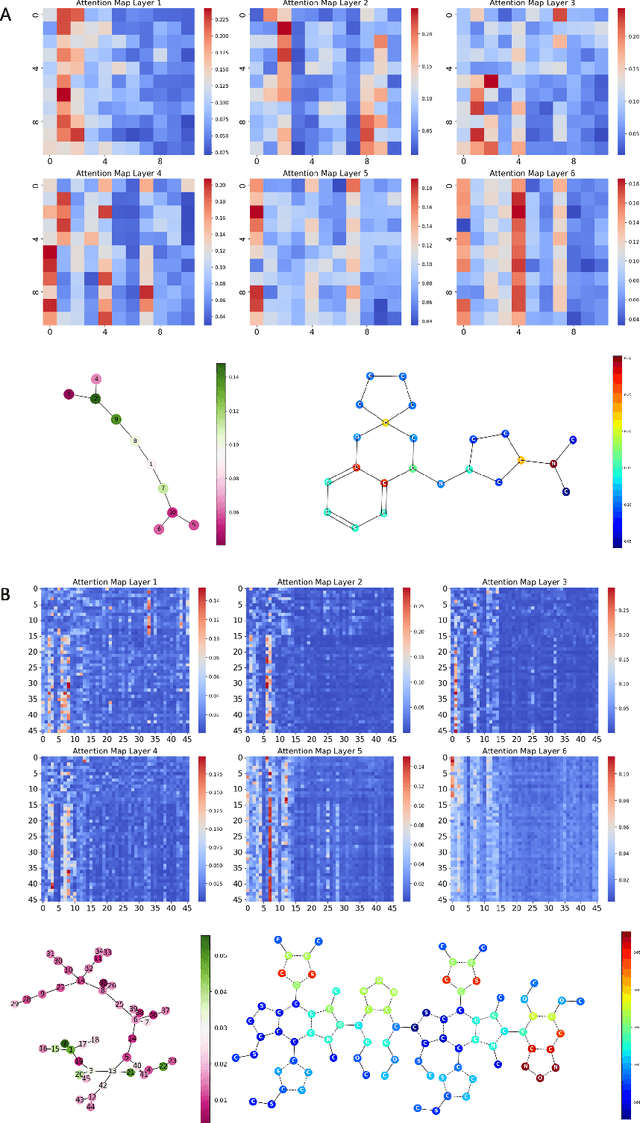
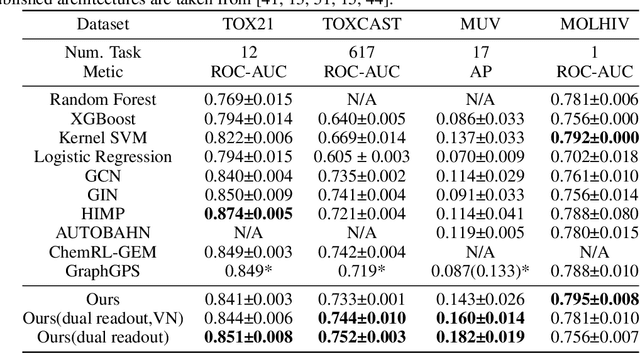
Transformers, adapted from natural language processing, are emerging as a leading approach for graph representation learning. Contemporary graph transformers often treat nodes or edges as separate tokens. This approach leads to computational challenges for even moderately-sized graphs due to the quadratic scaling of self-attention complexity with token count. In this paper, we introduce SubFormer, a graph transformer that operates on subgraphs that aggregate information by a message-passing mechanism. This approach reduces the number of tokens and enhances learning long-range interactions. We demonstrate SubFormer on benchmarks for predicting molecular properties from chemical structures and show that it is competitive with state-of-the-art graph transformers at a fraction of the computational cost, with training times on the order of minutes on a consumer-grade graphics card. We interpret the attention weights in terms of chemical structures. We show that SubFormer exhibits limited over-smoothing and avoids over-squashing, which is prevalent in traditional graph neural networks.

P-tensors: a General Formalism for Constructing Higher Order Message Passing Networks

Several recent papers have recently shown that higher order graph neural networks can achieve better accuracy than their standard message passing counterparts, especially on highly structured graphs such as molecules. These models typically work by considering higher order representations of subgraphs contained within a given graph and then perform some linear maps between them. We formalize these structures as permutation equivariant tensors, or P-tensors, and derive a basis for all linear maps between arbitrary order equivariant P-tensors. Experimentally, we demonstrate this paradigm achieves state of the art performance on several benchmark datasets.

Fast Temporal Wavelet Graph Neural Networks

Spatio-temporal signals forecasting plays an important role in numerous domains, especially in neuroscience and transportation. The task is challenging due to the highly intricate spatial structure, as well as the non-linear temporal dynamics of the network. To facilitate reliable and timely forecast for the human brain and traffic networks, we propose the Fast Temporal Wavelet Graph Neural Networks (FTWGNN) that is both time- and memory-efficient for learning tasks on timeseries data with the underlying graph structure, thanks to the theories of multiresolution analysis and wavelet theory on discrete spaces. We employ Multiresolution Matrix Factorization (MMF) (Kondor et al., 2014) to factorize the highly dense graph structure and compute the corresponding sparse wavelet basis that allows us to construct fast wavelet convolution as the backbone of our novel architecture. Experimental results on real-world PEMS-BAY, METR-LA traffic datasets and AJILE12 ECoG dataset show that FTWGNN is competitive with the state-of-the-arts while maintaining a low computational footprint. Our PyTorch implementation is publicly available at https://github.com/HySonLab/TWGNN.

Multiresolution Graph Transformers and Wavelet Positional Encoding for Learning Hierarchical Structures

Contemporary graph learning algorithms are not well-defined for large molecules since they do not consider the hierarchical interactions among the atoms, which are essential to determine the molecular properties of macromolecules. In this work, we propose Multiresolution Graph Transformers (MGT), the first graph transformer architecture that can learn to represent large molecules at multiple scales. MGT can learn to produce representations for the atoms and group them into meaningful functional groups or repeating units. We also introduce Wavelet Positional Encoding (WavePE), a new positional encoding method that can guarantee localization in both spectral and spatial domains. Our approach achieves competitive results on two macromolecule datasets consisting of polymers and peptides. Furthermore, the visualizations, including clustering results on macromolecules and low-dimensional spaces of their representations, demonstrate the capability of our methodology in learning to represent long-range and hierarchical structures. Our PyTorch implementation is publicly available at https://github.com/HySonLab/Multires-Graph-Transformer.

Modeling Polypharmacy and Predicting Drug-Drug Interactions using Deep Generative Models on Multimodal Graphs

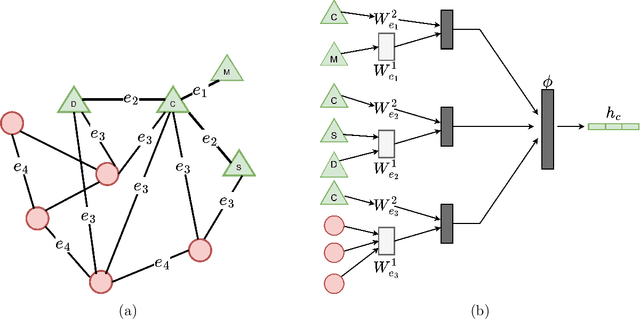
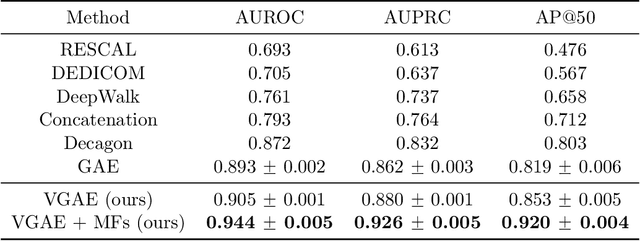
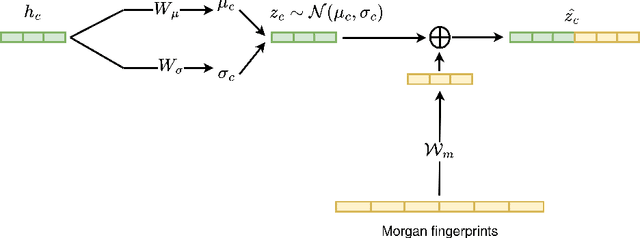
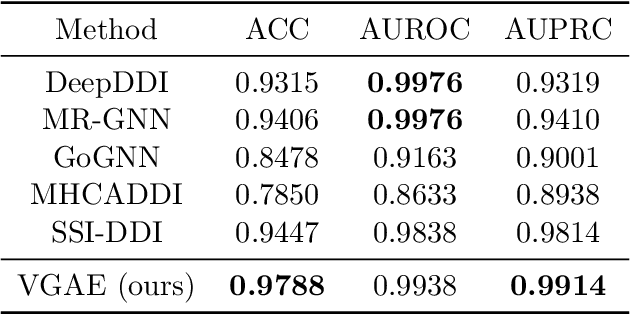
Latent representations of drugs and their targets produced by contemporary graph autoencoder models have proved useful in predicting many types of node-pair interactions on large networks, including drug-drug, drug-target, and target-target interactions. However, most existing approaches model either the node's latent spaces in which node distributions are rigid or do not effectively capture the interrelations between drugs; these limitations hinder the methods from accurately predicting drug-pair interactions. In this paper, we present the effectiveness of variational graph autoencoders (VGAE) in modeling latent node representations on multimodal networks. Our approach can produce flexible latent spaces for each node type of the multimodal graph; the embeddings are used later for predicting links among node pairs under different edge types. To further enhance the models' performance, we suggest a new method that concatenates Morgan fingerprints, which capture the molecular structures of each drug, with their latent embeddings before preceding them to the decoding stage for link prediction. Our proposed model shows competitive results on three multimodal networks: (1) a multimodal graph consisting of drug and protein nodes, (2) a multimodal graph constructed from a subset of the DrugBank database involving drug nodes under different interaction types, and (3) a multimodal graph consisting of drug and cell line nodes. Our source code is publicly available at https://github.com/HySonLab/drug-interactions.

Group-Equivariant Neural Networks with Fusion Diagrams

Many learning tasks in physics and chemistry involve global spatial symmetries as well as permutational symmetry between particles. The standard approach to such problems is equivariant neural networks, which employ tensor products between various tensors that transform under the spatial group. However, as the number of different tensors and the complexity of relationships between them increases, the bookkeeping associated with ensuring parsimony as well as equivariance quickly becomes nontrivial. In this paper, we propose to use fusion diagrams, a technique widely used in simulating SU($2$)-symmetric quantum many-body problems, to design new equivariant components for use in equivariant neural networks. This yields a diagrammatic approach to constructing new neural network architectures. We show that when applied to particles in a given local neighborhood, the resulting components, which we call fusion blocks, are universal approximators of any continuous equivariant function defined on the neighborhood. As a practical demonstration, we incorporate a fusion block into a pre-existing equivariant architecture (Cormorant) and show that it improves performance on benchmark molecular learning tasks.

Predicting Drug-Drug Interactions using Deep Generative Models on Graphs

Latent representations of drugs and their targets produced by contemporary graph autoencoder-based models have proved useful in predicting many types of node-pair interactions on large networks, including drug-drug, drug-target, and target-target interactions. However, most existing approaches model the node's latent spaces in which node distributions are rigid and disjoint; these limitations hinder the methods from generating new links among pairs of nodes. In this paper, we present the effectiveness of variational graph autoencoders (VGAE) in modeling latent node representations on multimodal networks. Our approach can produce flexible latent spaces for each node type of the multimodal graph; the embeddings are used later for predicting links among node pairs under different edge types. To further enhance the models' performance, we suggest a new method that concatenates Morgan fingerprints, which capture the molecular structures of each drug, with their latent embeddings before preceding them to the decoding stage for link prediction. Our proposed model shows competitive results on two multimodal networks: (1) a multi-graph consisting of drug and protein nodes, and (2) a multi-graph consisting of drug and cell line nodes. Our source code is publicly available at https://github.com/HySonLab/drug-interactions.