Model-Free Adversarial Purification via Coarse-To-Fine Tensor Network Representation

Deep neural networks are known to be vulnerable to well-designed adversarial attacks. Although numerous defense strategies have been proposed, many are tailored to the specific attacks or tasks and often fail to generalize across diverse scenarios. In this paper, we propose Tensor Network Purification (TNP), a novel model-free adversarial purification method by a specially designed tensor network decomposition algorithm. TNP depends neither on the pre-trained generative model nor the specific dataset, resulting in strong robustness across diverse adversarial scenarios. To this end, the key challenge lies in relaxing Gaussian-noise assumptions of classical decompositions and accommodating the unknown distribution of adversarial perturbations. Unlike the low-rank representation of classical decompositions, TNP aims to reconstruct the unobserved clean examples from an adversarial example. Specifically, TNP leverages progressive downsampling and introduces a novel adversarial optimization objective to address the challenge of minimizing reconstruction error but without inadvertently restoring adversarial perturbations. Extensive experiments conducted on CIFAR-10, CIFAR-100, and ImageNet demonstrate that our method generalizes effectively across various norm threats, attack types, and tasks, providing a versatile and promising adversarial purification technique.

Imputation of Time-varying Edge Flows in Graphs by Multilinear Kernel Regression and Manifold Learning

This paper extends the recently developed framework of multilinear kernel regression and imputation via manifold learning (MultiL-KRIM) to impute time-varying edge flows in a graph. MultiL-KRIM uses simplicial-complex arguments and Hodge Laplacians to incorporate the graph topology, and exploits manifold-learning arguments to identify latent geometries within features which are modeled as a point-cloud around a smooth manifold embedded in a reproducing kernel Hilbert space (RKHS). Following the concept of tangent spaces to smooth manifolds, linear approximating patches are used to add a collaborative-filtering flavor to the point-cloud approximations. Together with matrix factorizations, MultiL-KRIM effects dimensionality reduction, and enables efficient computations, without any training data or additional information. Numerical tests on real-network time-varying edge flows demonstrate noticeable improvements of MultiL-KRIM over several state-of-the-art schemes.

Multilinear Kernel Regression and Imputation via Manifold Learning

This paper introduces a novel nonparametric framework for data imputation, coined multilinear kernel regression and imputation via the manifold assumption (MultiL-KRIM). Motivated by manifold learning, MultiL-KRIM models data features as a point cloud located in or close to a user-unknown smooth manifold embedded in a reproducing kernel Hilbert space. Unlike typical manifold-learning routes, which seek low-dimensional patterns via regularizers based on graph-Laplacian matrices, MultiL-KRIM builds instead on the intuitive concept of tangent spaces to manifolds and incorporates collaboration among point-cloud neighbors (regressors) directly into the data-modeling term of the loss function. Multiple kernel functions are allowed to offer robustness and rich approximation properties, while multiple matrix factors offer low-rank modeling, integrate dimensionality reduction, and streamline computations with no need of training data. Two important application domains showcase the functionality of MultiL-KRIM: time-varying-graph-signal (TVGS) recovery, and reconstruction of highly accelerated dynamic-magnetic-resonance-imaging (dMRI) data. Extensive numerical tests on real and synthetic data demonstrate MultiL-KRIM's remarkable speedups over its predecessors, and outperformance over prevalent "shallow" data-imputation techniques, with a more intuitive and explainable pipeline than deep-image-prior methods.

Multi-Linear Kernel Regression and Imputation in Data Manifolds

This paper introduces an efficient multi-linear nonparametric (kernel-based) approximation framework for data regression and imputation, and its application to dynamic magnetic-resonance imaging (dMRI). Data features are assumed to reside in or close to a smooth manifold embedded in a reproducing kernel Hilbert space. Landmark points are identified to describe concisely the point cloud of features by linear approximating patches which mimic the concept of tangent spaces to smooth manifolds. The multi-linear model effects dimensionality reduction, enables efficient computations, and extracts data patterns and their geometry without any training data or additional information. Numerical tests on dMRI data under severe under-sampling demonstrate remarkable improvements in efficiency and accuracy of the proposed approach over its predecessors, popular data modeling methods, as well as recent tensor-based and deep-image-prior schemes.

Fast Temporal Wavelet Graph Neural Networks

Spatio-temporal signals forecasting plays an important role in numerous domains, especially in neuroscience and transportation. The task is challenging due to the highly intricate spatial structure, as well as the non-linear temporal dynamics of the network. To facilitate reliable and timely forecast for the human brain and traffic networks, we propose the Fast Temporal Wavelet Graph Neural Networks (FTWGNN) that is both time- and memory-efficient for learning tasks on timeseries data with the underlying graph structure, thanks to the theories of multiresolution analysis and wavelet theory on discrete spaces. We employ Multiresolution Matrix Factorization (MMF) (Kondor et al., 2014) to factorize the highly dense graph structure and compute the corresponding sparse wavelet basis that allows us to construct fast wavelet convolution as the backbone of our novel architecture. Experimental results on real-world PEMS-BAY, METR-LA traffic datasets and AJILE12 ECoG dataset show that FTWGNN is competitive with the state-of-the-arts while maintaining a low computational footprint. Our PyTorch implementation is publicly available at https://github.com/HySonLab/TWGNN.

Neural-Progressive Hedging: Enforcing Constraints in Reinforcement Learning with Stochastic Programming

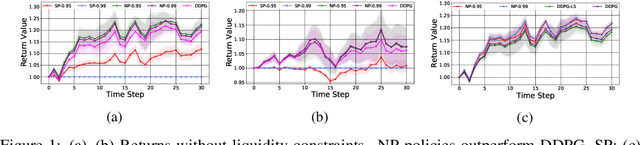
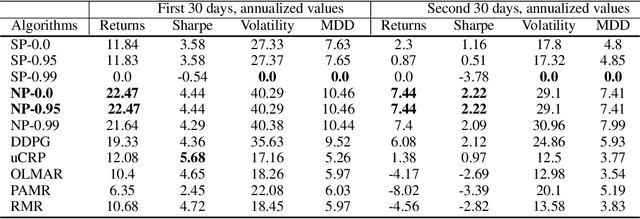
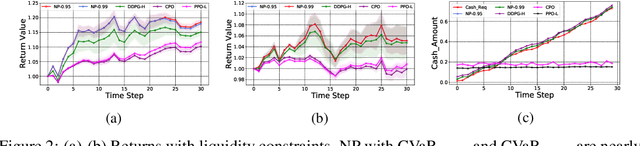
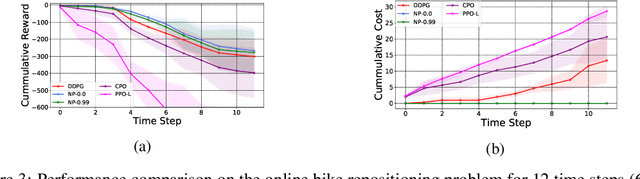
We propose a framework, called neural-progressive hedging (NP), that leverages stochastic programming during the online phase of executing a reinforcement learning (RL) policy. The goal is to ensure feasibility with respect to constraints and risk-based objectives such as conditional value-at-risk (CVaR) during the execution of the policy, using probabilistic models of the state transitions to guide policy adjustments. The framework is particularly amenable to the class of sequential resource allocation problems since feasibility with respect to typical resource constraints cannot be enforced in a scalable manner. The NP framework provides an alternative that adds modest overhead during the online phase. Experimental results demonstrate the efficacy of the NP framework on two continuous real-world tasks: (i) the portfolio optimization problem with liquidity constraints for financial planning, characterized by non-stationary state distributions; and (ii) the dynamic repositioning problem in bike sharing systems, that embodies the class of supply-demand matching problems. We show that the NP framework produces policies that are better than deep RL and other baseline approaches, adapting to non-stationarity, whilst satisfying structural constraints and accommodating risk measures in the resulting policies. Additional benefits of the NP framework are ease of implementation and better explainability of the policies.

Probabilistic Inference for Learning from Untrusted Sources

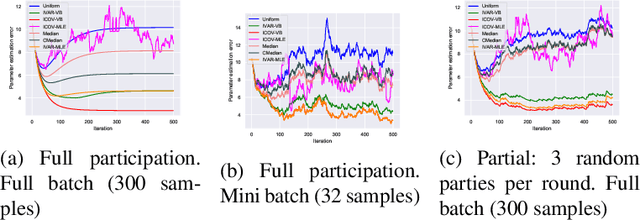
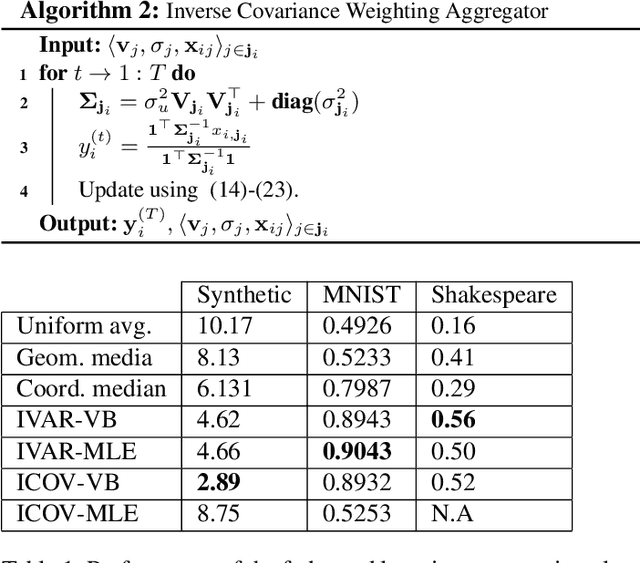
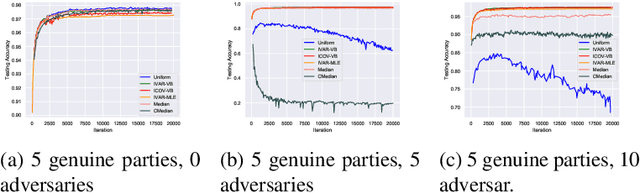
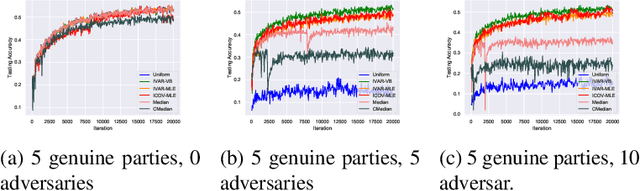
Federated learning brings potential benefits of faster learning, better solutions, and a greater propensity to transfer when heterogeneous data from different parties increases diversity. However, because federated learning tasks tend to be large and complex, and training times non-negligible, it is important for the aggregation algorithm to be robust to non-IID data and corrupted parties. This robustness relies on the ability to identify, and appropriately weight, incompatible parties. Recent work assumes that a \textit{reference dataset} is available through which to perform the identification. We consider settings where no such reference dataset is available; rather, the quality and suitability of the parties needs to be \textit{inferred}. We do so by bringing ideas from crowdsourced predictions and collaborative filtering, where one must infer an unknown ground truth given proposals from participants with unknown quality. We propose novel federated learning aggregation algorithms based on Bayesian inference that adapt to the quality of the parties. Empirically, we show that the algorithms outperform standard and robust aggregation in federated learning on both synthetic and real data.

Variational Bayesian Inference for Crowdsourcing Predictions

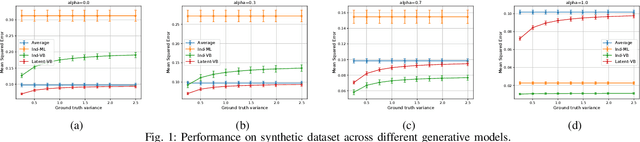
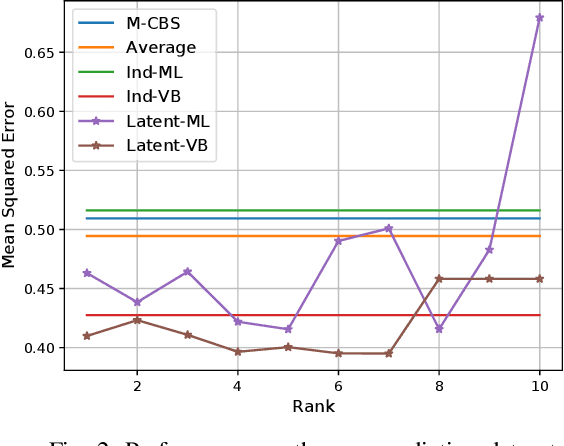
Crowdsourcing has emerged as an effective means for performing a number of machine learning tasks such as annotation and labelling of images and other data sets. In most early settings of crowdsourcing, the task involved classification, that is assigning one of a discrete set of labels to each task. Recently, however, more complex tasks have been attempted including asking crowdsource workers to assign continuous labels, or predictions. In essence, this involves the use of crowdsourcing for function estimation. We are motivated by this problem to drive applications such as collaborative prediction, that is, harnessing the wisdom of the crowd to predict quantities more accurately. To do so, we propose a Bayesian approach aimed specifically at alleviating overfitting, a typical impediment to accurate prediction models in practice. In particular, we develop a variational Bayesian technique for two different worker noise models - one that assumes workers' noises are independent and the other that assumes workers' noises have a latent low-rank structure. Our evaluations on synthetic and real-world datasets demonstrate that these Bayesian approaches perform significantly better than existing non-Bayesian approaches and are thus potentially useful for this class of crowdsourcing problems.

Policy Gradient With Value Function Approximation For Collective Multiagent Planning

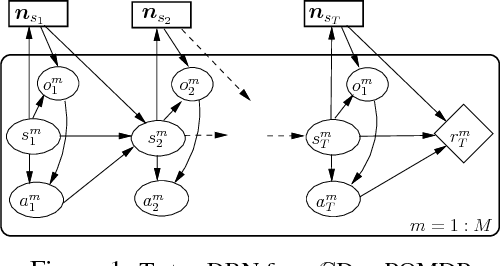
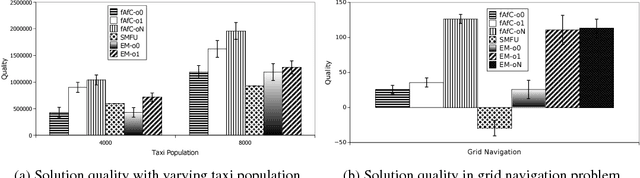
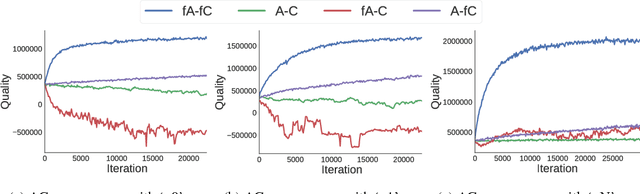
Decentralized (PO)MDPs provide an expressive framework for sequential decision making in a multiagent system. Given their computational complexity, recent research has focused on tractable yet practical subclasses of Dec-POMDPs. We address such a subclass called CDEC-POMDP where the collective behavior of a population of agents affects the joint-reward and environment dynamics. Our main contribution is an actor-critic (AC) reinforcement learning method for optimizing CDEC-POMDP policies. Vanilla AC has slow convergence for larger problems. To address this, we show how a particular decomposition of the approximate action-value function over agents leads to effective updates, and also derive a new way to train the critic based on local reward signals. Comparisons on a synthetic benchmark and a real-world taxi fleet optimization problem show that our new AC approach provides better quality solutions than previous best approaches.

Dynamic Stochastic Orienteering Problems for Risk-Aware Applications

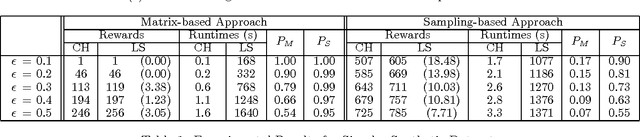
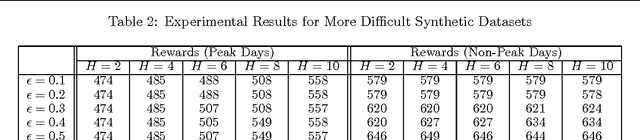
Orienteering problems (OPs) are a variant of the well-known prize-collecting traveling salesman problem, where the salesman needs to choose a subset of cities to visit within a given deadline. OPs and their extensions with stochastic travel times (SOPs) have been used to model vehicle routing problems and tourist trip design problems. However, they suffer from two limitations travel times between cities are assumed to be time independent and the route provided is independent of the risk preference (with respect to violating the deadline) of the user. To address these issues, we make the following contributions: We introduce (1) a dynamic SOP (DSOP) model, which is an extension of SOPs with dynamic (time-dependent) travel times; (2) a risk-sensitive criterion to allow for different risk preferences; and (3) a local search algorithm to solve DSOPs with this risk-sensitive criterion. We evaluated our algorithms on a real-world dataset for a theme park navigation problem as well as synthetic datasets employed in the literature.