Dynamic Stochastic Orienteering Problems for Risk-Aware Applications
Paper and Code
Oct 16, 2012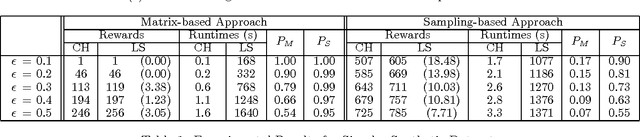

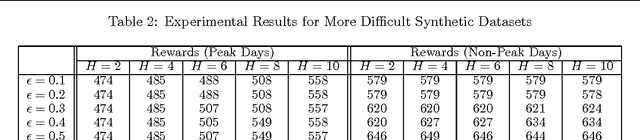
Orienteering problems (OPs) are a variant of the well-known prize-collecting traveling salesman problem, where the salesman needs to choose a subset of cities to visit within a given deadline. OPs and their extensions with stochastic travel times (SOPs) have been used to model vehicle routing problems and tourist trip design problems. However, they suffer from two limitations travel times between cities are assumed to be time independent and the route provided is independent of the risk preference (with respect to violating the deadline) of the user. To address these issues, we make the following contributions: We introduce (1) a dynamic SOP (DSOP) model, which is an extension of SOPs with dynamic (time-dependent) travel times; (2) a risk-sensitive criterion to allow for different risk preferences; and (3) a local search algorithm to solve DSOPs with this risk-sensitive criterion. We evaluated our algorithms on a real-world dataset for a theme park navigation problem as well as synthetic datasets employed in the literature.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge