Calibrating Uncertainty for Zero-Shot Adversarial CLIP

CLIP delivers strong zero-shot classification but remains highly vulnerable to adversarial attacks. Previous work of adversarial fine-tuning largely focuses on matching the predicted logits between clean and adversarial examples, which overlooks uncertainty calibration and may degrade the zero-shot generalization. A common expectation in reliable uncertainty estimation is that predictive uncertainty should increase as inputs become more difficult or shift away from the training distribution. However, we frequently observe the opposite in the adversarial setting: perturbations not only degrade accuracy but also suppress uncertainty, leading to severe miscalibration and unreliable over-confidence. This overlooked phenomenon highlights a critical reliability gap beyond robustness. To bridge this gap, we propose a novel adversarial fine-tuning objective for CLIP considering both prediction accuracy and uncertainty alignments. By reparameterizing the output of CLIP as the concentration parameter of a Dirichlet distribution, we propose a unified representation that captures relative semantic structure and the magnitude of predictive confidence. Our objective aligns these distributions holistically under perturbations, moving beyond single-logit anchoring and restoring calibrated uncertainty. Experiments on multiple zero-shot classification benchmarks demonstrate that our approach effectively restores calibrated uncertainty and achieves competitive adversarial robustness while maintaining clean accuracy.

Model-Free Adversarial Purification via Coarse-To-Fine Tensor Network Representation

Deep neural networks are known to be vulnerable to well-designed adversarial attacks. Although numerous defense strategies have been proposed, many are tailored to the specific attacks or tasks and often fail to generalize across diverse scenarios. In this paper, we propose Tensor Network Purification (TNP), a novel model-free adversarial purification method by a specially designed tensor network decomposition algorithm. TNP depends neither on the pre-trained generative model nor the specific dataset, resulting in strong robustness across diverse adversarial scenarios. To this end, the key challenge lies in relaxing Gaussian-noise assumptions of classical decompositions and accommodating the unknown distribution of adversarial perturbations. Unlike the low-rank representation of classical decompositions, TNP aims to reconstruct the unobserved clean examples from an adversarial example. Specifically, TNP leverages progressive downsampling and introduces a novel adversarial optimization objective to address the challenge of minimizing reconstruction error but without inadvertently restoring adversarial perturbations. Extensive experiments conducted on CIFAR-10, CIFAR-100, and ImageNet demonstrate that our method generalizes effectively across various norm threats, attack types, and tasks, providing a versatile and promising adversarial purification technique.

Transformed Low-rank Adaptation via Tensor Decomposition and Its Applications to Text-to-image Models

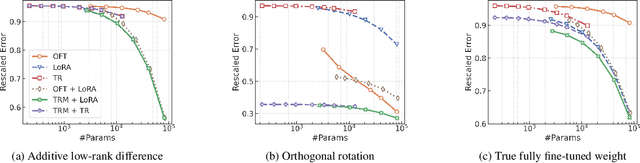
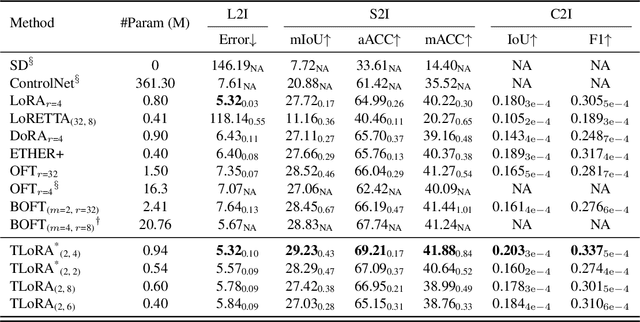
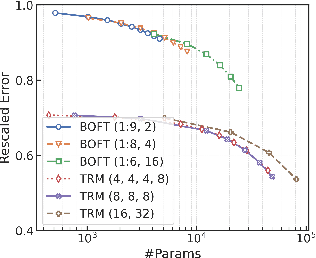
Parameter-Efficient Fine-Tuning (PEFT) of text-to-image models has become an increasingly popular technique with many applications. Among the various PEFT methods, Low-Rank Adaptation (LoRA) and its variants have gained significant attention due to their effectiveness, enabling users to fine-tune models with limited computational resources. However, the approximation gap between the low-rank assumption and desired fine-tuning weights prevents the simultaneous acquisition of ultra-parameter-efficiency and better performance. To reduce this gap and further improve the power of LoRA, we propose a new PEFT method that combines two classes of adaptations, namely, transform and residual adaptations. In specific, we first apply a full-rank and dense transform to the pre-trained weight. This learnable transform is expected to align the pre-trained weight as closely as possible to the desired weight, thereby reducing the rank of the residual weight. Then, the residual part can be effectively approximated by more compact and parameter-efficient structures, with a smaller approximation error. To achieve ultra-parameter-efficiency in practice, we design highly flexible and effective tensor decompositions for both the transform and residual adaptations. Additionally, popular PEFT methods such as DoRA can be summarized under this transform plus residual adaptation scheme. Experiments are conducted on fine-tuning Stable Diffusion models in subject-driven and controllable generation. The results manifest that our method can achieve better performances and parameter efficiency compared to LoRA and several baselines.

Tighnari: Multi-modal Plant Species Prediction Based on Hierarchical Cross-Attention Using Graph-Based and Vision Backbone-Extracted Features

Predicting plant species composition in specific spatiotemporal contexts plays an important role in biodiversity management and conservation, as well as in improving species identification tools. Our work utilizes 88,987 plant survey records conducted in specific spatiotemporal contexts across Europe. We also use the corresponding satellite images, time series data, climate time series, and other rasterized environmental data such as land cover, human footprint, bioclimatic, and soil variables as training data to train the model to predict the outcomes of 4,716 plant surveys. We propose a feature construction and result correction method based on the graph structure. Through comparative experiments, we select the best-performing backbone networks for feature extraction in both temporal and image modalities. In this process, we built a backbone network based on the Swin-Transformer Block for extracting temporal Cubes features. We then design a hierarchical cross-attention mechanism capable of robustly fusing features from multiple modalities. During training, we adopt a 10-fold cross-fusion method based on fine-tuning and use a Threshold Top-K method for post-processing. Ablation experiments demonstrate the improvements in model performance brought by our proposed solution pipeline.

Google is all you need: Semi-Supervised Transfer Learning Strategy For Light Multimodal Multi-Task Classification Model

As the volume of digital image data increases, the effectiveness of image classification intensifies. This study introduces a robust multi-label classification system designed to assign multiple labels to a single image, addressing the complexity of images that may be associated with multiple categories (ranging from 1 to 19, excluding 12). We propose a multi-modal classifier that merges advanced image recognition algorithms with Natural Language Processing (NLP) models, incorporating a fusion module to integrate these distinct modalities. The purpose of integrating textual data is to enhance the accuracy of label prediction by providing contextual understanding that visual analysis alone cannot fully capture. Our proposed classification model combines Convolutional Neural Networks (CNN) for image processing with NLP techniques for analyzing textual description (i.e., captions). This approach includes rigorous training and validation phases, with each model component verified and analyzed through ablation experiments. Preliminary results demonstrate the classifier's accuracy and efficiency, highlighting its potential as an automatic image-labeling system.

Best Transition Matrix Esitimation or Best Label Noise Robustness Classifier? Two Possible Methods to Enhance the Performance of T-revision

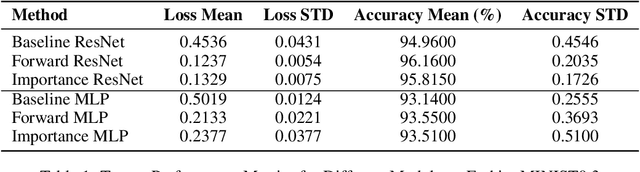
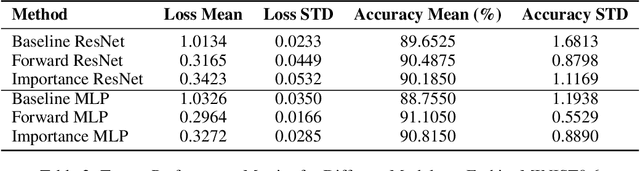
Label noise refers to incorrect labels in a dataset caused by human errors or collection defects, which is common in real-world applications and can significantly reduce the accuracy of models. This report explores how to estimate noise transition matrices and construct deep learning classifiers that are robust against label noise. In cases where the transition matrix is known, we apply forward correction and importance reweighting methods to correct the impact of label noise using the transition matrix. When the transition matrix is unknown or inaccurate, we use the anchor point assumption and T-Revision series methods to estimate or correct the noise matrix. In this study, we further improved the T-Revision method by developing T-Revision-Alpha and T-Revision-Softmax to enhance stability and robustness. Additionally, we designed and implemented two baseline classifiers, a Multi-Layer Perceptron (MLP) and ResNet-18, based on the cross-entropy loss function. We compared the performance of these methods on predicting clean labels and estimating transition matrices using the FashionMINIST dataset with known noise transition matrices. For the CIFAR-10 dataset, where the noise transition matrix is unknown, we estimated the noise matrix and evaluated the ability of the methods to predict clean labels.

nnY-Net: Swin-NeXt with Cross-Attention for 3D Medical Images Segmentation

This paper provides a novel 3D medical image segmentation model structure called nnY-Net. This name comes from the fact that our model adds a cross-attention module at the bottom of the U-net structure to form a Y structure. We integrate the advantages of the two latest SOTA models, MedNeXt and SwinUNETR, and use Swin Transformer as the encoder and ConvNeXt as the decoder to innovatively design the Swin-NeXt structure. Our model uses the lowest-level feature map of the encoder as Key and Value and uses patient features such as pathology and treatment information as Query to calculate the attention weights in a Cross Attention module. Moreover, we simplify some pre- and post-processing as well as data enhancement methods in 3D image segmentation based on the dynUnet and nnU-net frameworks. We integrate our proposed Swin-NeXt with Cross-Attention framework into this framework. Last, we construct a DiceFocalCELoss to improve the training efficiency for the uneven data convergence of voxel classification.

Scalable Bayesian Tensor Ring Factorization for Multiway Data Analysis

Tensor decompositions play a crucial role in numerous applications related to multi-way data analysis. By employing a Bayesian framework with sparsity-inducing priors, Bayesian Tensor Ring (BTR) factorization offers probabilistic estimates and an effective approach for automatically adapting the tensor ring rank during the learning process. However, previous BTR method employs an Automatic Relevance Determination (ARD) prior, which can lead to sub-optimal solutions. Besides, it solely focuses on continuous data, whereas many applications involve discrete data. More importantly, it relies on the Coordinate-Ascent Variational Inference (CAVI) algorithm, which is inadequate for handling large tensors with extensive observations. These limitations greatly limit its application scales and scopes, making it suitable only for small-scale problems, such as image/video completion. To address these issues, we propose a novel BTR model that incorporates a nonparametric Multiplicative Gamma Process (MGP) prior, known for its superior accuracy in identifying latent structures. To handle discrete data, we introduce the P\'olya-Gamma augmentation for closed-form updates. Furthermore, we develop an efficient Gibbs sampler for consistent posterior simulation, which reduces the computational complexity of previous VI algorithm by two orders, and an online EM algorithm that is scalable to extremely large tensors. To showcase the advantages of our model, we conduct extensive experiments on both simulation data and real-world applications.

A Unified Analysis for Finite Weight Averaging

Averaging iterations of Stochastic Gradient Descent (SGD) have achieved empirical success in training deep learning models, such as Stochastic Weight Averaging (SWA), Exponential Moving Average (EMA), and LAtest Weight Averaging (LAWA). Especially, with a finite weight averaging method, LAWA can attain faster convergence and better generalization. However, its theoretical explanation is still less explored since there are fundamental differences between finite and infinite settings. In this work, we first generalize SGD and LAWA as Finite Weight Averaging (FWA) and explain their advantages compared to SGD from the perspective of optimization and generalization. A key challenge is the inapplicability of traditional methods in the sense of expectation or optimal values for infinite-dimensional settings in analyzing FWA's convergence. Second, the cumulative gradients introduced by FWA introduce additional confusion to the generalization analysis, especially making it more difficult to discuss them under different assumptions. Extending the final iteration convergence analysis to the FWA, this paper, under a convexity assumption, establishes a convergence bound $\mathcal{O}(\log\left(\frac{T}{k}\right)/\sqrt{T})$, where $k\in[1, T/2]$ is a constant representing the last $k$ iterations. Compared to SGD with $\mathcal{O}(\log(T)/\sqrt{T})$, we prove theoretically that FWA has a faster convergence rate and explain the effect of the number of average points. In the generalization analysis, we find a recursive representation for bounding the cumulative gradient using mathematical induction. We provide bounds for constant and decay learning rates and the convex and non-convex cases to show the good generalization performance of FWA. Finally, experimental results on several benchmarks verify our theoretical results.

Robust Diffusion Models for Adversarial Purification

Diffusion models (DMs) based adversarial purification (AP) has shown to be the most powerful alternative to adversarial training (AT). However, these methods neglect the fact that pre-trained diffusion models themselves are not robust to adversarial attacks as well. Additionally, the diffusion process can easily destroy semantic information and generate a high quality image but totally different from the original input image after the reverse process, leading to degraded standard accuracy. To overcome these issues, a natural idea is to harness adversarial training strategy to retrain or fine-tune the pre-trained diffusion model, which is computationally prohibitive. We propose a novel robust reverse process with adversarial guidance, which is independent of given pre-trained DMs and avoids retraining or fine-tuning the DMs. This robust guidance can not only ensure to generate purified examples retaining more semantic content but also mitigate the accuracy-robustness trade-off of DMs for the first time, which also provides DM-based AP an efficient adaptive ability to new attacks. Extensive experiments are conducted to demonstrate that our method achieves the state-of-the-art results and exhibits generalization against different attacks.