Neural-Progressive Hedging: Enforcing Constraints in Reinforcement Learning with Stochastic Programming
Paper and Code
Feb 27, 2022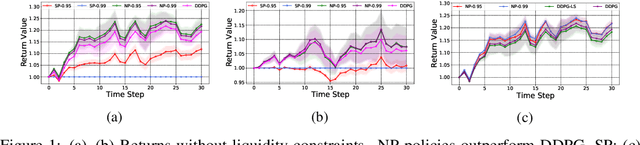
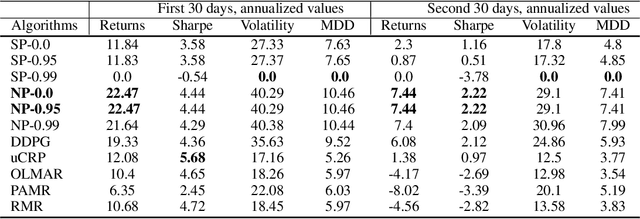
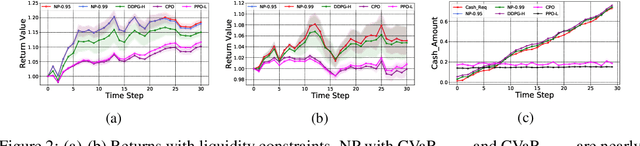
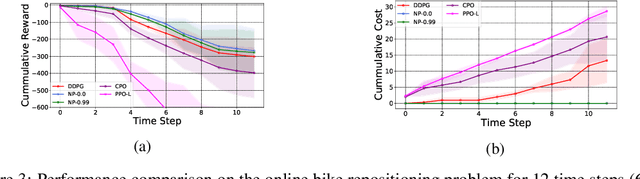
We propose a framework, called neural-progressive hedging (NP), that leverages stochastic programming during the online phase of executing a reinforcement learning (RL) policy. The goal is to ensure feasibility with respect to constraints and risk-based objectives such as conditional value-at-risk (CVaR) during the execution of the policy, using probabilistic models of the state transitions to guide policy adjustments. The framework is particularly amenable to the class of sequential resource allocation problems since feasibility with respect to typical resource constraints cannot be enforced in a scalable manner. The NP framework provides an alternative that adds modest overhead during the online phase. Experimental results demonstrate the efficacy of the NP framework on two continuous real-world tasks: (i) the portfolio optimization problem with liquidity constraints for financial planning, characterized by non-stationary state distributions; and (ii) the dynamic repositioning problem in bike sharing systems, that embodies the class of supply-demand matching problems. We show that the NP framework produces policies that are better than deep RL and other baseline approaches, adapting to non-stationarity, whilst satisfying structural constraints and accommodating risk measures in the resulting policies. Additional benefits of the NP framework are ease of implementation and better explainability of the policies.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge