Technical Report: The Graph Spectral Token -- Enhancing Graph Transformers with Spectral Information

Graph Transformers have emerged as a powerful alternative to Message-Passing Graph Neural Networks (MP-GNNs) to address limitations such as over-squashing of information exchange. However, incorporating graph inductive bias into transformer architectures remains a significant challenge. In this report, we propose the Graph Spectral Token, a novel approach to directly encode graph spectral information, which captures the global structure of the graph, into the transformer architecture. By parameterizing the auxiliary [CLS] token and leaving other tokens representing graph nodes, our method seamlessly integrates spectral information into the learning process. We benchmark the effectiveness of our approach by enhancing two existing graph transformers, GraphTrans and SubFormer. The improved GraphTrans, dubbed GraphTrans-Spec, achieves over 10% improvements on large graph benchmark datasets while maintaining efficiency comparable to MP-GNNs. SubFormer-Spec demonstrates strong performance across various datasets.

Transformers are efficient hierarchical chemical graph learners

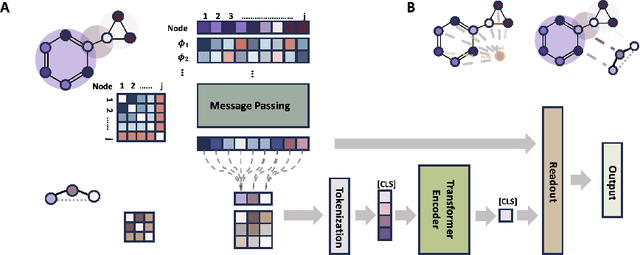
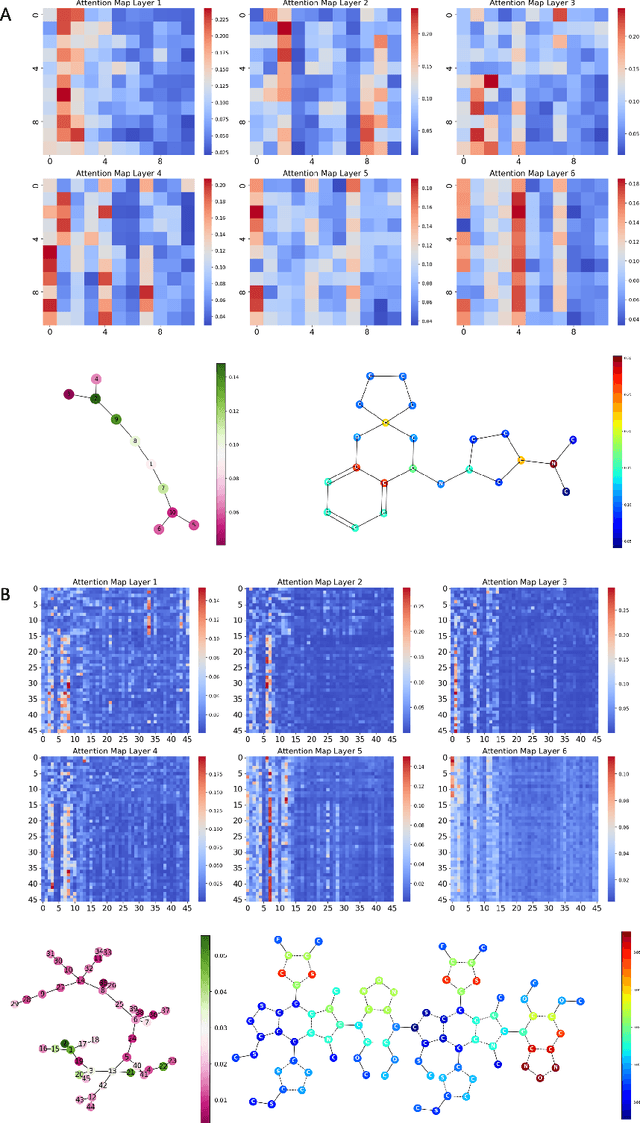
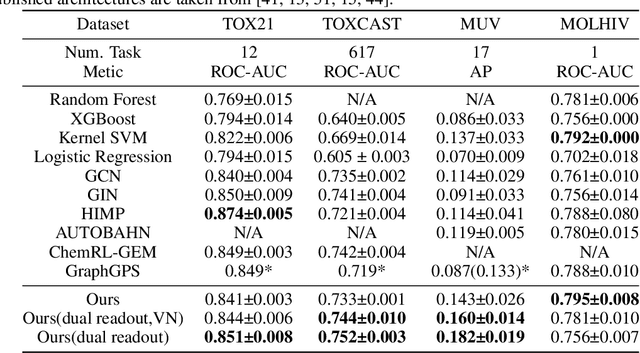
Transformers, adapted from natural language processing, are emerging as a leading approach for graph representation learning. Contemporary graph transformers often treat nodes or edges as separate tokens. This approach leads to computational challenges for even moderately-sized graphs due to the quadratic scaling of self-attention complexity with token count. In this paper, we introduce SubFormer, a graph transformer that operates on subgraphs that aggregate information by a message-passing mechanism. This approach reduces the number of tokens and enhances learning long-range interactions. We demonstrate SubFormer on benchmarks for predicting molecular properties from chemical structures and show that it is competitive with state-of-the-art graph transformers at a fraction of the computational cost, with training times on the order of minutes on a consumer-grade graphics card. We interpret the attention weights in terms of chemical structures. We show that SubFormer exhibits limited over-smoothing and avoids over-squashing, which is prevalent in traditional graph neural networks.

R-Mixup: Riemannian Mixup for Biological Networks

Biological networks are commonly used in biomedical and healthcare domains to effectively model the structure of complex biological systems with interactions linking biological entities. However, due to their characteristics of high dimensionality and low sample size, directly applying deep learning models on biological networks usually faces severe overfitting. In this work, we propose R-MIXUP, a Mixup-based data augmentation technique that suits the symmetric positive definite (SPD) property of adjacency matrices from biological networks with optimized training efficiency. The interpolation process in R-MIXUP leverages the log-Euclidean distance metrics from the Riemannian manifold, effectively addressing the swelling effect and arbitrarily incorrect label issues of vanilla Mixup. We demonstrate the effectiveness of R-MIXUP with five real-world biological network datasets on both regression and classification tasks. Besides, we derive a commonly ignored necessary condition for identifying the SPD matrices of biological networks and empirically study its influence on the model performance. The code implementation can be found in Appendix E.

Group-Equivariant Neural Networks with Fusion Diagrams

Many learning tasks in physics and chemistry involve global spatial symmetries as well as permutational symmetry between particles. The standard approach to such problems is equivariant neural networks, which employ tensor products between various tensors that transform under the spatial group. However, as the number of different tensors and the complexity of relationships between them increases, the bookkeeping associated with ensuring parsimony as well as equivariance quickly becomes nontrivial. In this paper, we propose to use fusion diagrams, a technique widely used in simulating SU($2$)-symmetric quantum many-body problems, to design new equivariant components for use in equivariant neural networks. This yields a diagrammatic approach to constructing new neural network architectures. We show that when applied to particles in a given local neighborhood, the resulting components, which we call fusion blocks, are universal approximators of any continuous equivariant function defined on the neighborhood. As a practical demonstration, we incorporate a fusion block into a pre-existing equivariant architecture (Cormorant) and show that it improves performance on benchmark molecular learning tasks.

On the Super-exponential Quantum Speedup of Equivariant Quantum Machine Learning Algorithms with SU Symmetry

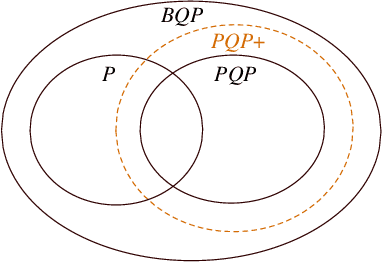
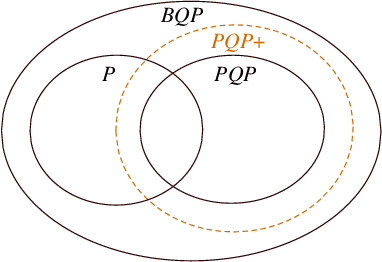
We introduce a framework of the equivariant convolutional algorithms which is tailored for a number of machine-learning tasks on physical systems with arbitrary SU($d$) symmetries. It allows us to enhance a natural model of quantum computation--permutational quantum computing (PQC) [Quantum Inf. Comput., 10, 470-497 (2010)] --and defines a more powerful model: PQC+. While PQC was shown to be effectively classically simulatable, we exhibit a problem which can be efficiently solved on PQC+ machine, whereas the best known classical algorithms runs in $O(n!n^2)$ time, thus providing strong evidence against PQC+ being classically simulatable. We further discuss practical quantum machine learning algorithms which can be carried out in the paradigm of PQC+.

Speeding up Learning Quantum States through Group Equivariant Convolutional Quantum Ans{ä}tze

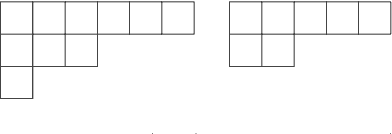
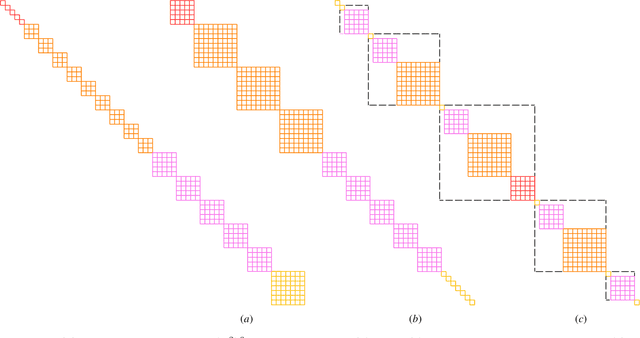
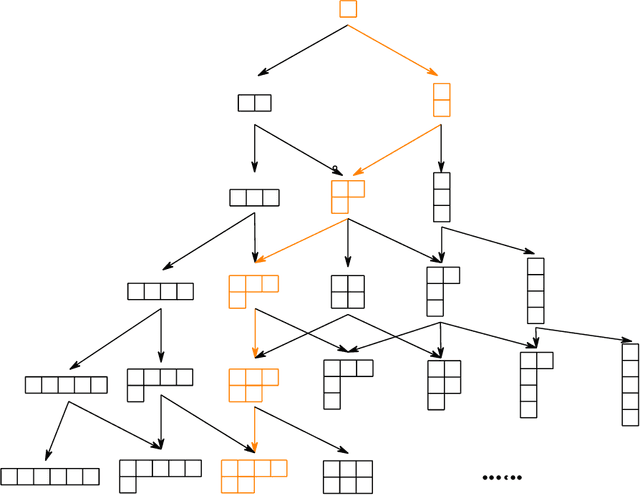
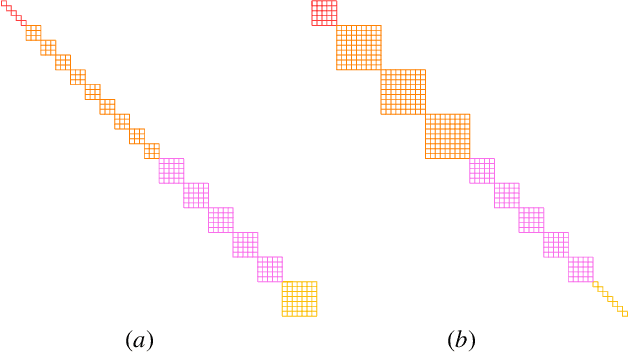
We develop a theoretical framework for $S_n$-equivariant quantum convolutional circuits, building on and significantly generalizing Jordan's Permutational Quantum Computing (PQC) formalism. We show that quantum circuits are a natural choice for Fourier space neural architectures affording a super-exponential speedup in computing the matrix elements of $S_n$-Fourier coefficients compared to the best known classical Fast Fourier Transform (FFT) over the symmetric group. In particular, we utilize the Okounkov-Vershik approach to prove Harrow's statement (Ph.D. Thesis 2005 p.160) on the equivalence between $\operatorname{SU}(d)$- and $S_n$-irrep bases and to establish the $S_n$-equivariant Convolutional Quantum Alternating Ans{\"a}tze ($S_n$-CQA) using Young-Jucys-Murphy (YJM) elements. We prove that $S_n$-CQA are dense, thus expressible within each $S_n$-irrep block, which may serve as a universal model for potential future quantum machine learning and optimization applications. Our method provides another way to prove the universality of Quantum Approximate Optimization Algorithm (QAOA), from the representation-theoretical point of view. Our framework can be naturally applied to a wide array of problems with global $\operatorname{SU}(d)$ symmetry. We present numerical simulations to showcase the effectiveness of the ans{\"a}tze to find the sign structure of the ground state of the $J_1$--$J_2$ antiferromagnetic Heisenberg model on the rectangular and Kagome lattices. Our work identifies quantum advantage for a specific machine learning problem, and provides the first application of the celebrated Okounkov-Vershik's representation theory to machine learning and quantum physics.