On the Super-exponential Quantum Speedup of Equivariant Quantum Machine Learning Algorithms with SU Symmetry

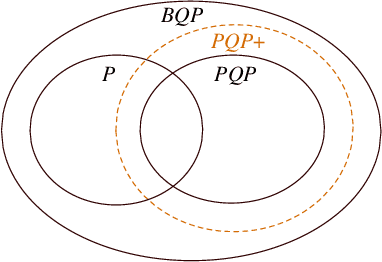
We introduce a framework of the equivariant convolutional algorithms which is tailored for a number of machine-learning tasks on physical systems with arbitrary SU($d$) symmetries. It allows us to enhance a natural model of quantum computation--permutational quantum computing (PQC) [Quantum Inf. Comput., 10, 470-497 (2010)] --and defines a more powerful model: PQC+. While PQC was shown to be effectively classically simulatable, we exhibit a problem which can be efficiently solved on PQC+ machine, whereas the best known classical algorithms runs in $O(n!n^2)$ time, thus providing strong evidence against PQC+ being classically simulatable. We further discuss practical quantum machine learning algorithms which can be carried out in the paradigm of PQC+.