On the Super-exponential Quantum Speedup of Equivariant Quantum Machine Learning Algorithms with SU Symmetry

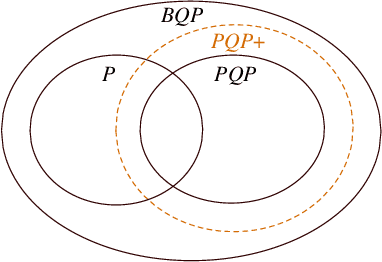
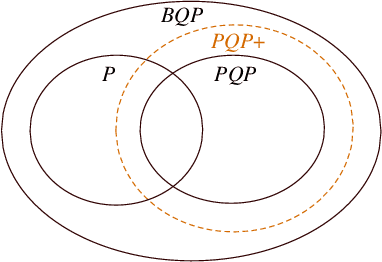
We introduce a framework of the equivariant convolutional algorithms which is tailored for a number of machine-learning tasks on physical systems with arbitrary SU($d$) symmetries. It allows us to enhance a natural model of quantum computation--permutational quantum computing (PQC) [Quantum Inf. Comput., 10, 470-497 (2010)] --and defines a more powerful model: PQC+. While PQC was shown to be effectively classically simulatable, we exhibit a problem which can be efficiently solved on PQC+ machine, whereas the best known classical algorithms runs in $O(n!n^2)$ time, thus providing strong evidence against PQC+ being classically simulatable. We further discuss practical quantum machine learning algorithms which can be carried out in the paradigm of PQC+.

Speeding up Learning Quantum States through Group Equivariant Convolutional Quantum Ans{ä}tze

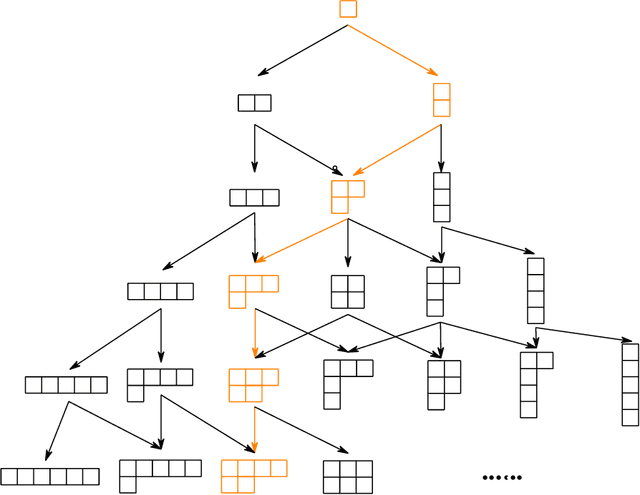
We develop a theoretical framework for $S_n$-equivariant quantum convolutional circuits, building on and significantly generalizing Jordan's Permutational Quantum Computing (PQC) formalism. We show that quantum circuits are a natural choice for Fourier space neural architectures affording a super-exponential speedup in computing the matrix elements of $S_n$-Fourier coefficients compared to the best known classical Fast Fourier Transform (FFT) over the symmetric group. In particular, we utilize the Okounkov-Vershik approach to prove Harrow's statement (Ph.D. Thesis 2005 p.160) on the equivalence between $\operatorname{SU}(d)$- and $S_n$-irrep bases and to establish the $S_n$-equivariant Convolutional Quantum Alternating Ans{\"a}tze ($S_n$-CQA) using Young-Jucys-Murphy (YJM) elements. We prove that $S_n$-CQA are dense, thus expressible within each $S_n$-irrep block, which may serve as a universal model for potential future quantum machine learning and optimization applications. Our method provides another way to prove the universality of Quantum Approximate Optimization Algorithm (QAOA), from the representation-theoretical point of view. Our framework can be naturally applied to a wide array of problems with global $\operatorname{SU}(d)$ symmetry. We present numerical simulations to showcase the effectiveness of the ans{\"a}tze to find the sign structure of the ground state of the $J_1$--$J_2$ antiferromagnetic Heisenberg model on the rectangular and Kagome lattices. Our work identifies quantum advantage for a specific machine learning problem, and provides the first application of the celebrated Okounkov-Vershik's representation theory to machine learning and quantum physics.

Learning hard quantum distributions with variational autoencoders

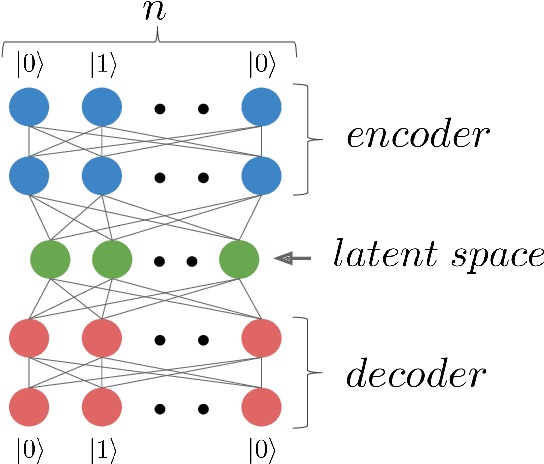
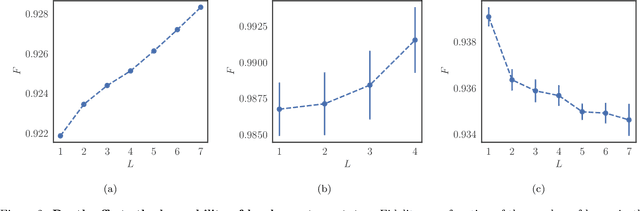
Studying general quantum many-body systems is one of the major challenges in modern physics because it requires an amount of computational resources that scales exponentially with the size of the system.Simulating the evolution of a state, or even storing its description, rapidly becomes intractable for exact classical algorithms. Recently, machine learning techniques, in the form of restricted Boltzmann machines, have been proposed as a way to efficiently represent certain quantum states with applications in state tomography and ground state estimation. Here, we introduce a new representation of states based on variational autoencoders. Variational autoencoders are a type of generative model in the form of a neural network. We probe the power of this representation by encoding probability distributions associated with states from different classes. Our simulations show that deep networks give a better representation for states that are hard to sample from, while providing no benefit for random states. This suggests that the probability distributions associated to hard quantum states might have a compositional structure that can be exploited by layered neural networks. Specifically, we consider the learnability of a class of quantum states introduced by Fefferman and Umans. Such states are provably hard to sample for classical computers, but not for quantum ones, under plausible computational complexity assumptions. The good level of compression achieved for hard states suggests these methods can be suitable for characterising states of the size expected in first generation quantum hardware.