Speeding up Learning Quantum States through Group Equivariant Convolutional Quantum Ans{ä}tze

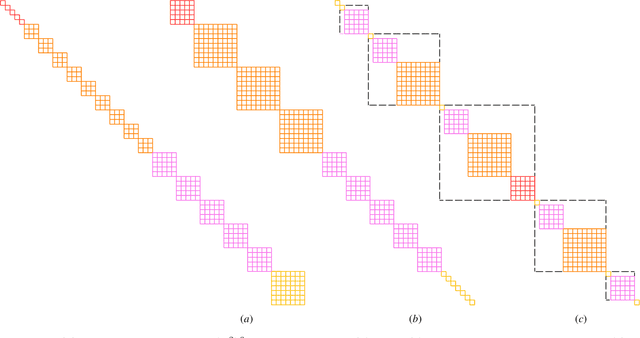
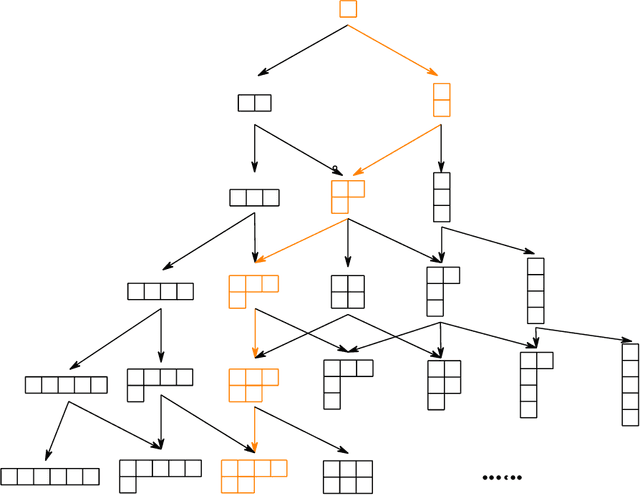
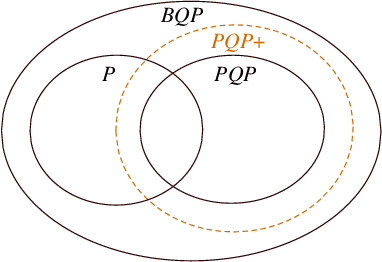
We develop a theoretical framework for $S_n$-equivariant quantum convolutional circuits, building on and significantly generalizing Jordan's Permutational Quantum Computing (PQC) formalism. We show that quantum circuits are a natural choice for Fourier space neural architectures affording a super-exponential speedup in computing the matrix elements of $S_n$-Fourier coefficients compared to the best known classical Fast Fourier Transform (FFT) over the symmetric group. In particular, we utilize the Okounkov-Vershik approach to prove Harrow's statement (Ph.D. Thesis 2005 p.160) on the equivalence between $\operatorname{SU}(d)$- and $S_n$-irrep bases and to establish the $S_n$-equivariant Convolutional Quantum Alternating Ans{\"a}tze ($S_n$-CQA) using Young-Jucys-Murphy (YJM) elements. We prove that $S_n$-CQA are dense, thus expressible within each $S_n$-irrep block, which may serve as a universal model for potential future quantum machine learning and optimization applications. Our method provides another way to prove the universality of Quantum Approximate Optimization Algorithm (QAOA), from the representation-theoretical point of view. Our framework can be naturally applied to a wide array of problems with global $\operatorname{SU}(d)$ symmetry. We present numerical simulations to showcase the effectiveness of the ans{\"a}tze to find the sign structure of the ground state of the $J_1$--$J_2$ antiferromagnetic Heisenberg model on the rectangular and Kagome lattices. Our work identifies quantum advantage for a specific machine learning problem, and provides the first application of the celebrated Okounkov-Vershik's representation theory to machine learning and quantum physics.