Quantum statistics from classical simulations via generative Gibbs sampling

Accurate simulation of nuclear quantum effects is essential for molecular modeling but expensive using path integral molecular dynamics (PIMD). We present GG-PI, a ring-polymer-based framework that combines generative modeling of the single-bead conditional density with Gibbs sampling to recover quantum statistics from classical simulation data. GG-PI uses inexpensive standard classical simulations or existing data for training and allows transfer across temperatures without retraining. On standard test systems, GG-PI significantly reduces wall clock time compared to PIMD. Our approach extends easily to a wide range of problems with similar Markov structure.

Mitigating mode collapse in normalizing flows by annealing with an adaptive schedule: Application to parameter estimation

Normalizing flows (NFs) provide uncorrelated samples from complex distributions, making them an appealing tool for parameter estimation. However, the practical utility of NFs remains limited by their tendency to collapse to a single mode of a multimodal distribution. In this study, we show that annealing with an adaptive schedule based on the effective sample size (ESS) can mitigate mode collapse. We demonstrate that our approach can converge the marginal likelihood for a biochemical oscillator model fit to time-series data in ten-fold less computation time than a widely used ensemble Markov chain Monte Carlo (MCMC) method. We show that the ESS can also be used to reduce variance by pruning the samples. We expect these developments to be of general use for sampling with NFs and discuss potential opportunities for further improvements.

geom2vec: pretrained GNNs as geometric featurizers for conformational dynamics

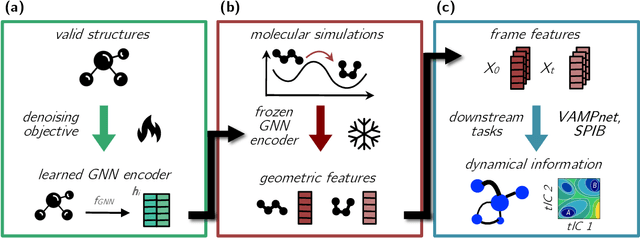
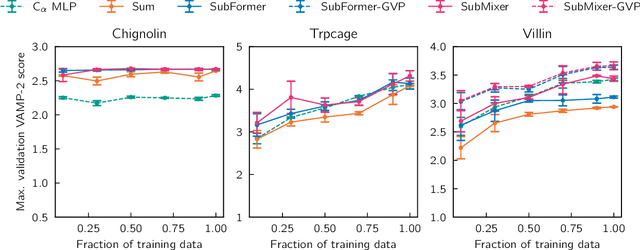
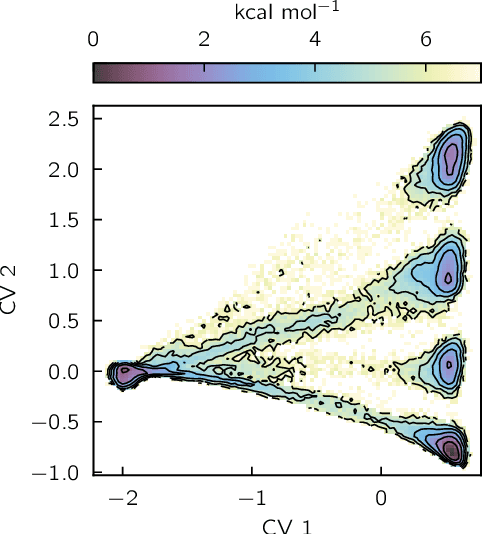
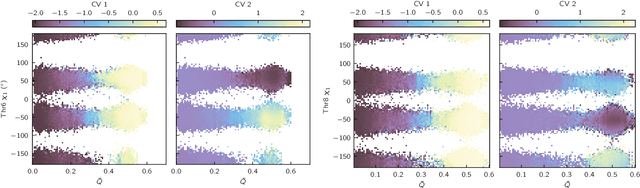
Identifying informative low-dimensional features that characterize dynamics in molecular simulations remains a challenge, often requiring extensive hand-tuning and system-specific knowledge. Here, we introduce geom2vec, in which pretrained graph neural networks (GNNs) are used as universal geometric featurizers. By pretraining equivariant GNNs on a large dataset of molecular conformations with a self-supervised denoising objective, we learn transferable structural representations that capture molecular geometric patterns without further fine-tuning. We show that the learned representations can be directly used to analyze trajectory data, thus eliminating the need for manual feature selection and improving robustness of the simulation analysis workflows. Importantly, by decoupling GNN training from training for downstream tasks, we enable analysis of larger molecular graphs with limited computational resources.

Transformers are efficient hierarchical chemical graph learners

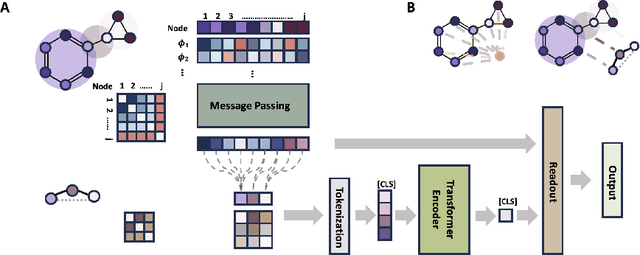
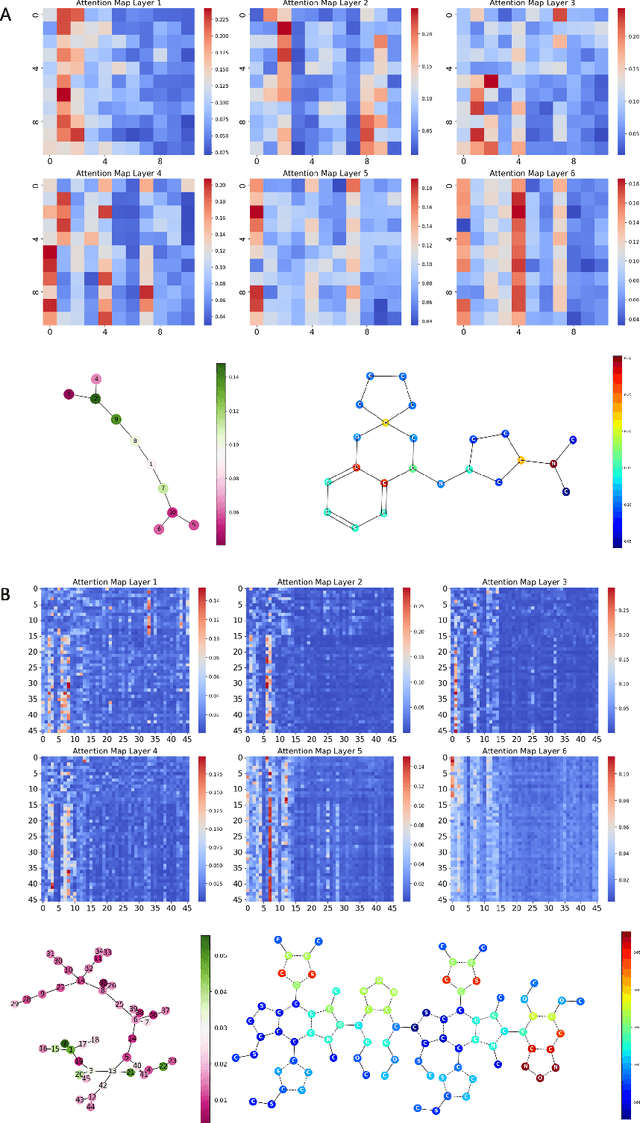
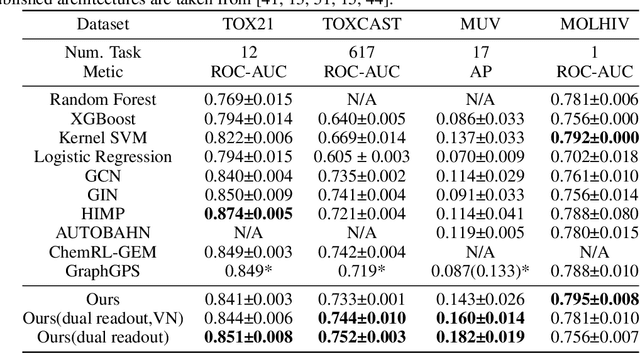
Transformers, adapted from natural language processing, are emerging as a leading approach for graph representation learning. Contemporary graph transformers often treat nodes or edges as separate tokens. This approach leads to computational challenges for even moderately-sized graphs due to the quadratic scaling of self-attention complexity with token count. In this paper, we introduce SubFormer, a graph transformer that operates on subgraphs that aggregate information by a message-passing mechanism. This approach reduces the number of tokens and enhances learning long-range interactions. We demonstrate SubFormer on benchmarks for predicting molecular properties from chemical structures and show that it is competitive with state-of-the-art graph transformers at a fraction of the computational cost, with training times on the order of minutes on a consumer-grade graphics card. We interpret the attention weights in terms of chemical structures. We show that SubFormer exhibits limited over-smoothing and avoids over-squashing, which is prevalent in traditional graph neural networks.

Inexact iterative numerical linear algebra for neural network-based spectral estimation and rare-event prediction

Understanding dynamics in complex systems is challenging because there are many degrees of freedom, and those that are most important for describing events of interest are often not obvious. The leading eigenfunctions of the transition operator are useful for visualization, and they can provide an efficient basis for computing statistics such as the likelihood and average time of events (predictions). Here we develop inexact iterative linear algebra methods for computing these eigenfunctions (spectral estimation) and making predictions from a data set of short trajectories sampled at finite intervals. We demonstrate the methods on a low-dimensional model that facilitates visualization and a high-dimensional model of a biomolecular system. Implications for the prediction problem in reinforcement learning are discussed.