Jonathan Weare
Quantum statistics from classical simulations via generative Gibbs sampling
Jan 28, 2026Abstract:Accurate simulation of nuclear quantum effects is essential for molecular modeling but expensive using path integral molecular dynamics (PIMD). We present GG-PI, a ring-polymer-based framework that combines generative modeling of the single-bead conditional density with Gibbs sampling to recover quantum statistics from classical simulation data. GG-PI uses inexpensive standard classical simulations or existing data for training and allows transfer across temperatures without retraining. On standard test systems, GG-PI significantly reduces wall clock time compared to PIMD. Our approach extends easily to a wide range of problems with similar Markov structure.
AI-boosted rare event sampling to characterize extreme weather
Oct 31, 2025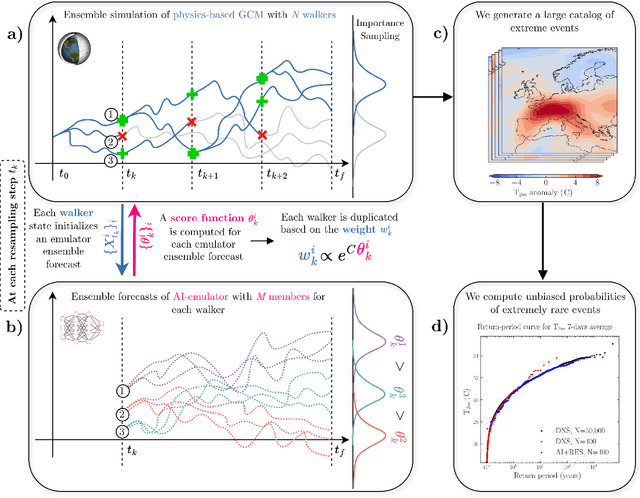
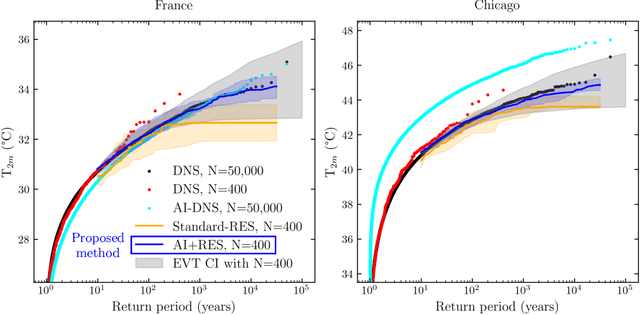
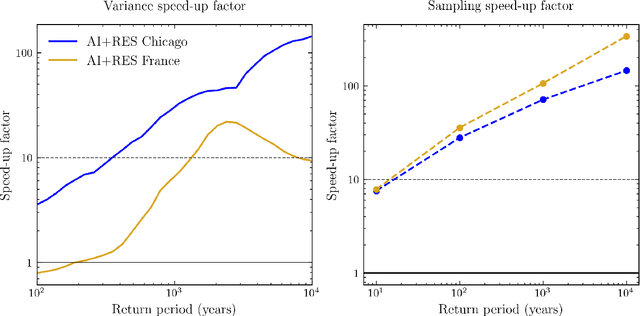
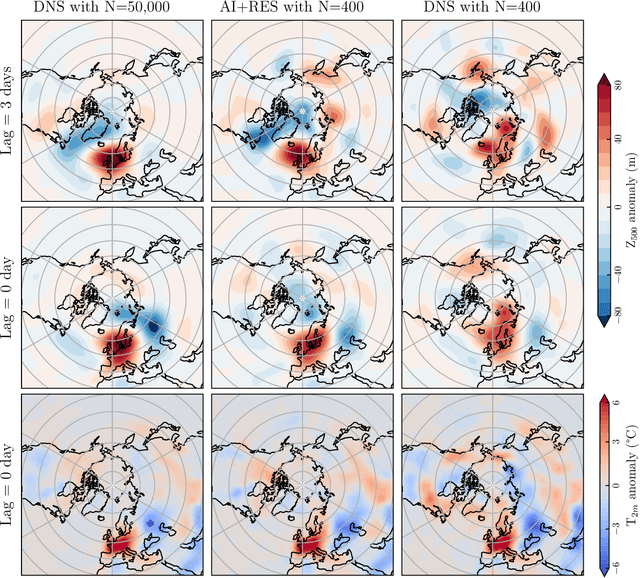
Abstract:Assessing the frequency and intensity of extreme weather events, and understanding how climate change affects them, is crucial for developing effective adaptation and mitigation strategies. However, observational datasets are too short and physics-based global climate models (GCMs) are too computationally expensive to obtain robust statistics for the rarest, yet most impactful, extreme events. AI-based emulators have shown promise for predictions at weather and even climate timescales, but they struggle on extreme events with few or no examples in their training dataset. Rare event sampling (RES) algorithms have previously demonstrated success for some extreme events, but their performance depends critically on a hard-to-identify "score function", which guides efficient sampling by a GCM. Here, we develop a novel algorithm, AI+RES, which uses ensemble forecasts of an AI weather emulator as the score function to guide highly efficient resampling of the GCM and generate robust (physics-based) extreme weather statistics and associated dynamics at 30-300x lower cost. We demonstrate AI+RES on mid-latitude heatwaves, a challenging test case requiring a score function with predictive skill many days in advance. AI+RES, which synergistically integrates AI, RES, and GCMs, offers a powerful, scalable tool for studying extreme events in climate science, as well as other disciplines in science and engineering where rare events and AI emulators are active areas of research.
Can AI weather models predict out-of-distribution gray swan tropical cyclones?
Oct 19, 2024



Abstract:Predicting gray swan weather extremes, which are possible but so rare that they are absent from the training dataset, is a major concern for AI weather/climate models. An important open question is whether AI models can extrapolate from weaker weather events present in the training set to stronger, unseen weather extremes. To test this, we train independent versions of the AI model FourCastNet on the 1979-2015 ERA5 dataset with all data, or with Category 3-5 tropical cyclones (TCs) removed, either globally or only over the North Atlantic or Western Pacific basin. We then test these versions of FourCastNet on 2018-2023 Category 5 TCs (gray swans). All versions yield similar accuracy for global weather, but the one trained without Category 3-5 TCs cannot accurately forecast Category 5 TCs, indicating that these models cannot extrapolate from weaker storms. The versions trained without Category 3-5 TCs in one basin show some skill forecasting Category 5 TCs in that basin, suggesting that FourCastNet can generalize across tropical basins. This is encouraging and surprising because regional information is implicitly encoded in inputs. No version satisfies gradient-wind balance, implying that enforcing such physical constraints may not improve generalizability to gray swans. Given that current state-of-the-art AI weather/climate models have similar learning strategies, we expect our findings to apply to other models and extreme events. Our work demonstrates that novel learning strategies are needed for AI weather/climate models to provide early warning or estimated statistics for the rarest, most impactful weather extremes.
geom2vec: pretrained GNNs as geometric featurizers for conformational dynamics
Sep 30, 2024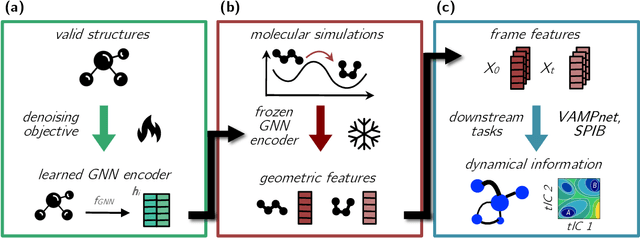
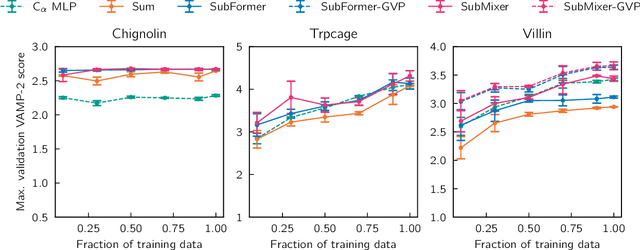
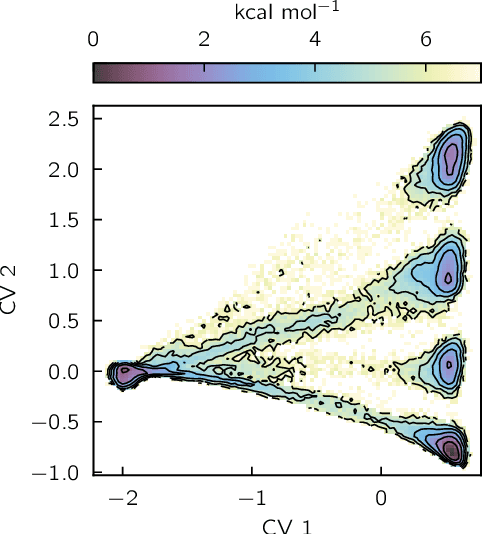
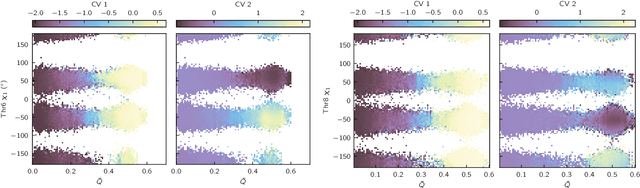
Abstract:Identifying informative low-dimensional features that characterize dynamics in molecular simulations remains a challenge, often requiring extensive hand-tuning and system-specific knowledge. Here, we introduce geom2vec, in which pretrained graph neural networks (GNNs) are used as universal geometric featurizers. By pretraining equivariant GNNs on a large dataset of molecular conformations with a self-supervised denoising objective, we learn transferable structural representations that capture molecular geometric patterns without further fine-tuning. We show that the learned representations can be directly used to analyze trajectory data, thus eliminating the need for manual feature selection and improving robustness of the simulation analysis workflows. Importantly, by decoupling GNN training from training for downstream tasks, we enable analysis of larger molecular graphs with limited computational resources.
Convergence of Unadjusted Langevin in High Dimensions: Delocalization of Bias
Aug 20, 2024Abstract:The unadjusted Langevin algorithm is commonly used to sample probability distributions in extremely high-dimensional settings. However, existing analyses of the algorithm for strongly log-concave distributions suggest that, as the dimension $d$ of the problem increases, the number of iterations required to ensure convergence within a desired error in the $W_2$ metric scales in proportion to $d$ or $\sqrt{d}$. In this paper, we argue that, despite this poor scaling of the $W_2$ error for the full set of variables, the behavior for a small number of variables can be significantly better: a number of iterations proportional to $K$, up to logarithmic terms in $d$, often suffices for the algorithm to converge to within a desired $W_2$ error for all $K$-marginals. We refer to this effect as delocalization of bias. We show that the delocalization effect does not hold universally and prove its validity for Gaussian distributions and strongly log-concave distributions with certain sparse interactions. Our analysis relies on a novel $W_{2,\ell^\infty}$ metric to measure convergence. A key technical challenge we address is the lack of a one-step contraction property in this metric. Finally, we use asymptotic arguments to explore potential generalizations of the delocalization effect beyond the Gaussian and sparse interactions setting.
The surprising efficiency of temporal difference learning for rare event prediction
May 27, 2024



Abstract:We quantify the efficiency of temporal difference (TD) learning over the direct, or Monte Carlo (MC), estimator for policy evaluation in reinforcement learning, with an emphasis on estimation of quantities related to rare events. Policy evaluation is complicated in the rare event setting by the long timescale of the event and by the need for \emph{relative accuracy} in estimates of very small values. Specifically, we focus on least-squares TD (LSTD) prediction for finite state Markov chains, and show that LSTD can achieve relative accuracy far more efficiently than MC. We prove a central limit theorem for the LSTD estimator and upper bound the \emph{relative asymptotic variance} by simple quantities characterizing the connectivity of states relative to the transition probabilities between them. Using this bound, we show that, even when both the timescale of the rare event and the relative accuracy of the MC estimator are exponentially large in the number of states, LSTD maintains a fixed level of relative accuracy with a total number of observed transitions of the Markov chain that is only \emph{polynomially} large in the number of states.
Using Explainable AI and Transfer Learning to understand and predict the maintenance of Atlantic blocking with limited observational data
Apr 12, 2024Abstract:Blocking events are an important cause of extreme weather, especially long-lasting blocking events that trap weather systems in place. The duration of blocking events is, however, underestimated in climate models. Explainable Artificial Intelligence are a class of data analysis methods that can help identify physical causes of prolonged blocking events and diagnose model deficiencies. We demonstrate this approach on an idealized quasigeostrophic model developed by Marshall and Molteni (1993). We train a convolutional neural network (CNN), and subsequently, build a sparse predictive model for the persistence of Atlantic blocking, conditioned on an initial high-pressure anomaly. Shapley Additive ExPlanation (SHAP) analysis reveals that high-pressure anomalies in the American Southeast and North Atlantic, separated by a trough over Atlantic Canada, contribute significantly to prediction of sustained blocking events in the Atlantic region. This agrees with previous work that identified precursors in the same regions via wave train analysis. When we apply the same CNN to blockings in the ERA5 atmospheric reanalysis, there is insufficient data to accurately predict persistent blocks. We partially overcome this limitation by pre-training the CNN on the plentiful data of the Marshall-Molteni model, and then using Transfer Learning to achieve better predictions than direct training. SHAP analysis before and after transfer learning allows a comparison between the predictive features in the reanalysis and the quasigeostrophic model, quantifying dynamical biases in the idealized model. This work demonstrates the potential for machine learning methods to extract meaningful precursors of extreme weather events and achieve better prediction using limited observational data.
Improved Active Learning via Dependent Leverage Score Sampling
Oct 08, 2023Abstract:We show how to obtain improved active learning methods in the agnostic (adversarial noise) setting by combining marginal leverage score sampling with non-independent sampling strategies that promote spatial coverage. In particular, we propose an easily implemented method based on the pivotal sampling algorithm, which we test on problems motivated by learning-based methods for parametric PDEs and uncertainty quantification. In comparison to independent sampling, our method reduces the number of samples needed to reach a given target accuracy by up to $50\%$. We support our findings with two theoretical results. First, we show that any non-independent leverage score sampling method that obeys a weak one-sided $\ell_{\infty}$ independence condition (which includes pivotal sampling) can actively learn $d$ dimensional linear functions with $O(d\log d)$ samples, matching independent sampling. This result extends recent work on matrix Chernoff bounds under $\ell_{\infty}$ independence, and may be of interest for analyzing other sampling strategies beyond pivotal sampling. Second, we show that, for the important case of polynomial regression, our pivotal method obtains an improved bound of $O(d)$ samples.
Inexact iterative numerical linear algebra for neural network-based spectral estimation and rare-event prediction
Mar 22, 2023Abstract:Understanding dynamics in complex systems is challenging because there are many degrees of freedom, and those that are most important for describing events of interest are often not obvious. The leading eigenfunctions of the transition operator are useful for visualization, and they can provide an efficient basis for computing statistics such as the likelihood and average time of events (predictions). Here we develop inexact iterative linear algebra methods for computing these eigenfunctions (spectral estimation) and making predictions from a data set of short trajectories sampled at finite intervals. We demonstrate the methods on a low-dimensional model that facilitates visualization and a high-dimensional model of a biomolecular system. Implications for the prediction problem in reinforcement learning are discussed.
Understanding and eliminating spurious modes in variational Monte Carlo using collective variables
Nov 11, 2022Abstract:The use of neural network parametrizations to represent the ground state in variational Monte Carlo (VMC) calculations has generated intense interest in recent years. However, as we demonstrate in the context of the periodic Heisenberg spin chain, this approach can produce unreliable wave function approximations. One of the most obvious signs of failure is the occurrence of random, persistent spikes in the energy estimate during training. These energy spikes are caused by regions of configuration space that are over-represented by the wave function density, which are called ``spurious modes'' in the machine learning literature. After exploring these spurious modes in detail, we demonstrate that a collective-variable-based penalization yields a substantially more robust training procedure, preventing the formation of spurious modes and improving the accuracy of energy estimates. Because the penalization scheme is cheap to implement and is not specific to the particular model studied here, it can be extended to other applications of VMC where a reasonable choice of collective variable is available.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge