Adaptive Momentum and Nonlinear Damping for Neural Network Training

We propose a continuous-time scheme for large-scale optimization that introduces individual, adaptive momentum coefficients regulated by the kinetic energy of each model parameter. This approach automatically adjusts to local landscape curvature to maintain stability without sacrificing convergence speed. We demonstrate that our adaptive friction can be related to cubic damping, a suppression mechanism from structural dynamics. Furthermore, we introduce two specific optimization schemes by augmenting the continuous dynamics of mSGD and Adam with a cubic damping term. Empirically, our methods demonstrate robustness and match or outperform Adam on training ViT, BERT, and GPT2 tasks where mSGD typically struggles. We further provide theoretical results establishing the exponential convergence of the proposed schemes.

Adaptive Stepsizing for Stochastic Gradient Langevin Dynamics in Bayesian Neural Networks

Bayesian neural networks (BNNs) require scalable sampling algorithms to approximate posterior distributions over parameters. Existing stochastic gradient Markov Chain Monte Carlo (SGMCMC) methods are highly sensitive to the choice of stepsize and adaptive variants such as pSGLD typically fail to sample the correct invariant measure without addition of a costly divergence correction term. In this work, we build on the recently proposed `SamAdams' framework for timestep adaptation (Leimkuhler, Lohmann, and Whalley 2025), introducing an adaptive scheme: SA-SGLD, which employs time rescaling to modulate the stepsize according to a monitored quantity (typically the local gradient norm). SA-SGLD can automatically shrink stepsizes in regions of high curvature and expand them in flatter regions, improving both stability and mixing without introducing bias. We show that our method can achieve more accurate posterior sampling than SGLD on high-curvature 2D toy examples and in image classification with BNNs using sharp priors.

A Langevin sampling algorithm inspired by the Adam optimizer

We present a framework for adaptive-stepsize MCMC sampling based on time-rescaled Langevin dynamics, in which the stepsize variation is dynamically driven by an additional degree of freedom. Our approach augments the phase space by an additional variable which in turn defines a time reparameterization. The use of an auxiliary relaxation equation allows accumulation of a moving average of a local monitor function and provides for precise control of the timestep while circumventing the need to modify the drift term in the physical system. Our algorithm is straightforward to implement and can be readily combined with any off-the-peg fixed-stepsize Langevin integrator. As a particular example, we consider control of the stepsize by monitoring the norm of the log-posterior gradient, which takes inspiration from the Adam optimizer, the stepsize being automatically reduced in regions of steep change of the log posterior and increased on plateaus, improving numerical stability and convergence speed. As in Adam, the stepsize variation depends on the recent history of the gradient norm, which enhances stability and improves accuracy compared to more immediate control approaches. We demonstrate the potential benefit of this method--both in accuracy and in stability--in numerical experiments including Neal's funnel and a Bayesian neural network for classification of MNIST data.

Unbiased Kinetic Langevin Monte Carlo with Inexact Gradients

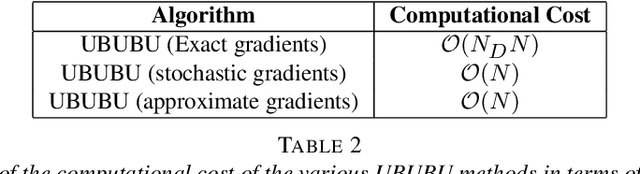
We present an unbiased method for Bayesian posterior means based on kinetic Langevin dynamics that combines advanced splitting methods with enhanced gradient approximations. Our approach avoids Metropolis correction by coupling Markov chains at different discretization levels in a multilevel Monte Carlo approach. Theoretical analysis demonstrates that our proposed estimator is unbiased, attains finite variance, and satisfies a central limit theorem. It can achieve accuracy $\epsilon>0$ for estimating expectations of Lipschitz functions in $d$ dimensions with $\mathcal{O}(d^{1/4}\epsilon^{-2})$ expected gradient evaluations, without assuming warm start. We exhibit similar bounds using both approximate and stochastic gradients, and our method's computational cost is shown to scale logarithmically with the size of the dataset. The proposed method is tested using a multinomial regression problem on the MNIST dataset and a Poisson regression model for soccer scores. Experiments indicate that the number of gradient evaluations per effective sample is independent of dimension, even when using inexact gradients. For product distributions, we give dimension-independent variance bounds. Our results demonstrate that the unbiased algorithm we present can be much more efficient than the ``gold-standard" randomized Hamiltonian Monte Carlo.

Multirate Training of Neural Networks

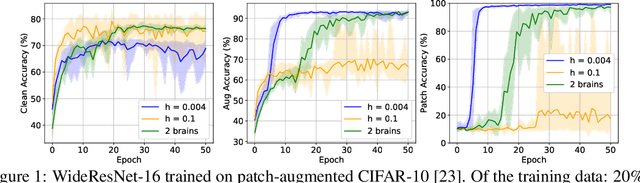
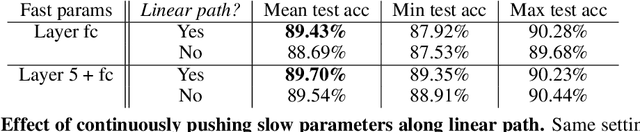
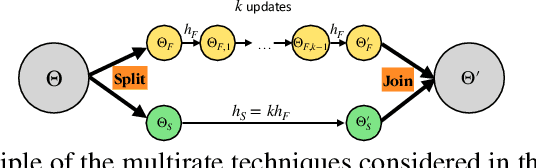
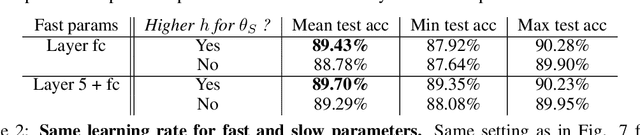
We propose multirate training of neural networks: partitioning neural network parameters into "fast" and "slow" parts which are trained simultaneously using different learning rates. By choosing appropriate partitionings we can obtain large computational speed-ups for transfer learning tasks. We show that for various transfer learning applications in vision and NLP we can fine-tune deep neural networks in almost half the time, without reducing the generalization performance of the resulting model. We also discuss other splitting choices for the neural network parameters which are beneficial in enhancing generalization performance in settings where neural networks are trained from scratch. Finally, we propose an additional multirate technique which can learn different features present in the data by training the full network on different time scales simultaneously. The benefits of using this approach are illustrated for ResNet architectures on image data. Our paper unlocks the potential of using multirate techniques for neural network training and provides many starting points for future work in this area.

Better Training using Weight-Constrained Stochastic Dynamics

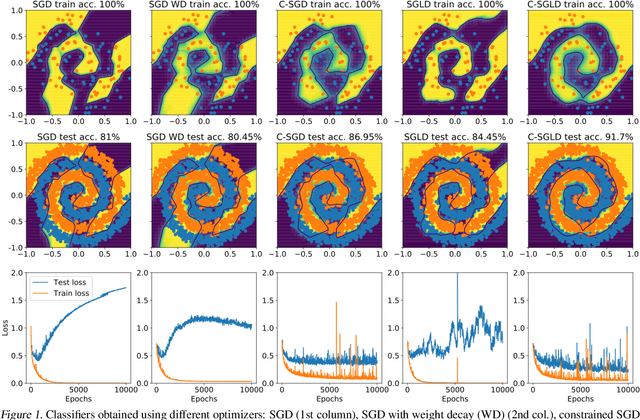
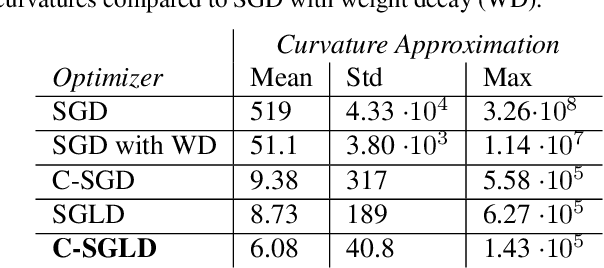
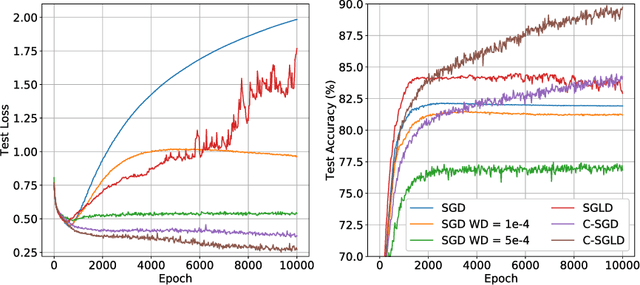
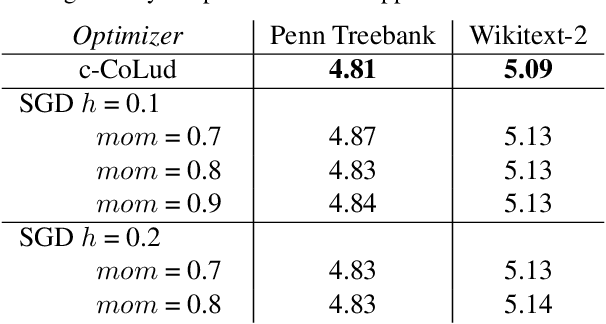
We employ constraints to control the parameter space of deep neural networks throughout training. The use of customized, appropriately designed constraints can reduce the vanishing/exploding gradients problem, improve smoothness of classification boundaries, control weight magnitudes and stabilize deep neural networks, and thus enhance the robustness of training algorithms and the generalization capabilities of neural networks. We provide a general approach to efficiently incorporate constraints into a stochastic gradient Langevin framework, allowing enhanced exploration of the loss landscape. We also present specific examples of constrained training methods motivated by orthogonality preservation for weight matrices and explicit weight normalizations. Discretization schemes are provided both for the overdamped formulation of Langevin dynamics and the underdamped form, in which momenta further improve sampling efficiency. These optimization schemes can be used directly, without needing to adapt neural network architecture design choices or to modify the objective with regularization terms, and see performance improvements in classification tasks.

Constraint-Based Regularization of Neural Networks

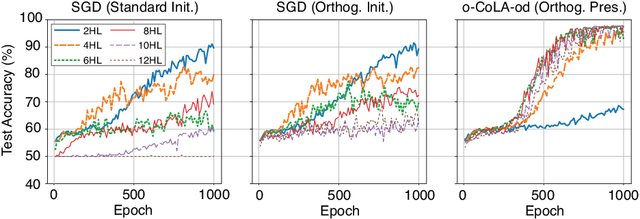
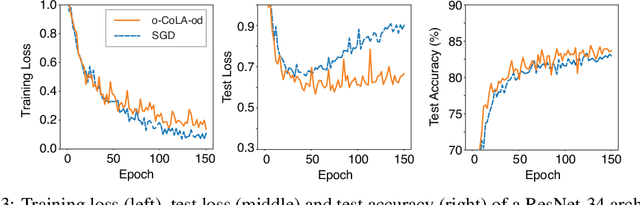
We propose a method for efficiently incorporating constraints into a stochastic gradient Langevin framework for the training of deep neural networks. Constraints allow direct control of the parameter space of the model. Appropriately designed, they reduce the vanishing/exploding gradient problem, control weight magnitudes and stabilize deep neural networks and thus improve the robustness of training algorithms and the generalization capabilities of the trained neural network. We present examples of constrained training methods motivated by orthogonality preservation for weight matrices and explicit weight normalizations. We describe the methods in the overdamped formulation of Langevin dynamics and the underdamped form, in which momenta help to improve sampling efficiency. The methods are explored in test examples in image classification and natural language processing.

Partitioned integrators for thermodynamic parameterization of neural networks

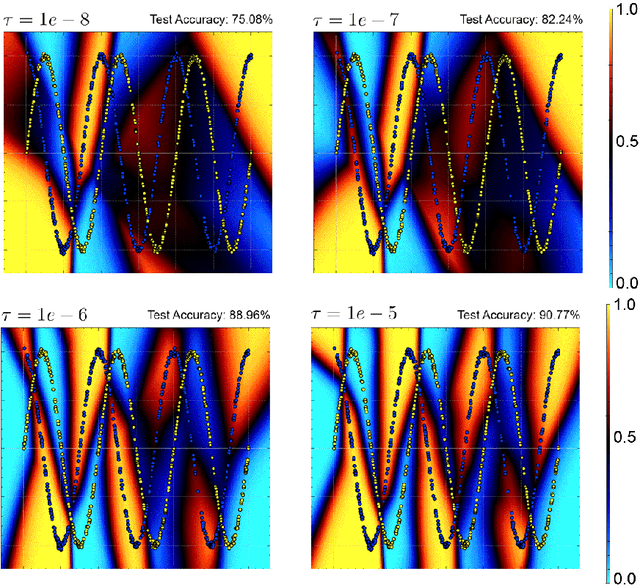
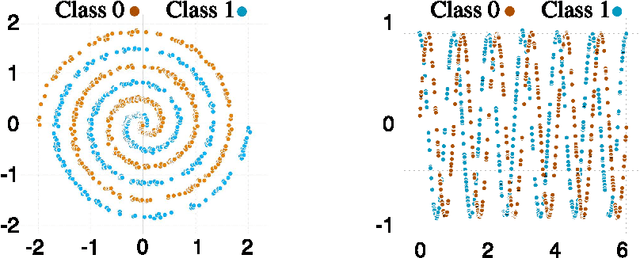
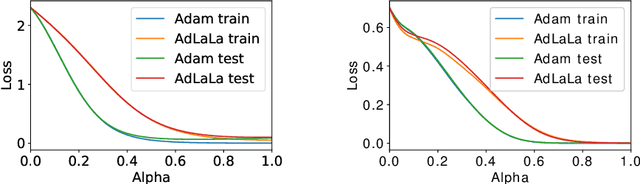
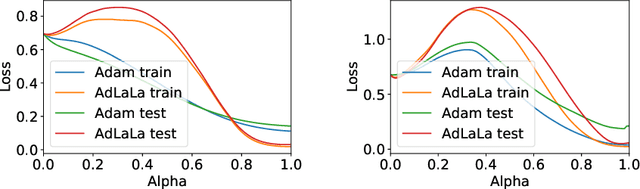
Stochastic Gradient Langevin Dynamics, the "unadjusted Langevin algorithm", and Adaptive Langevin Dynamics (also known as Stochastic Gradient Nos\'{e}-Hoover dynamics) are examples of existing thermodynamic parameterization methods in use for machine learning, but these can be substantially improved. We find that by partitioning the parameters based on natural layer structure we obtain schemes with rapid convergence for data sets with complicated loss landscapes. We describe easy-to-implement hybrid partitioned numerical algorithms, based on discretized stochastic differential equations, which are adapted to feed-forward neural networks, including LaLa (a multi-layer Langevin algorithm), AdLaLa (combining the adaptive Langevin and Langevin algorithms) and LOL (combining Langevin and Overdamped Langevin); we examine the convergence of these methods using numerical studies and compare their performance among themselves and in relation to standard alternatives such as stochastic gradient descent and ADAM. We present evidence that thermodynamic parameterization methods can be (i) faster, (ii) more accurate, and (iii) more robust than standard algorithms incorporated into machine learning frameworks, in particular for data sets with complicated loss landscapes. Moreover, we show in numerical studies that methods based on sampling excite many degrees of freedom. The equipartition property, which is a consequence of their ergodicity, means that these methods keep in play an ensemble of low-loss states during the training process. By drawing parameter states from a sufficiently rich distribution of nearby candidate states, we show that the thermodynamic schemes produce smoother classifiers, improve generalization and reduce overfitting compared to traditional optimizers.

TATi-Thermodynamic Analytics ToolkIt: TensorFlow-based software for posterior sampling in machine learning applications

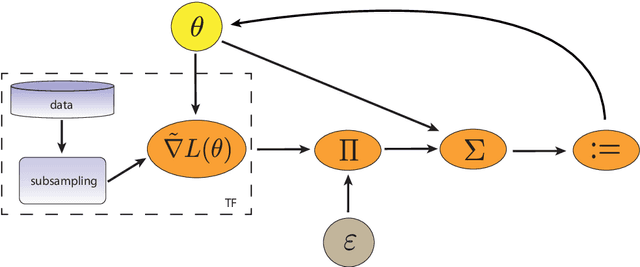
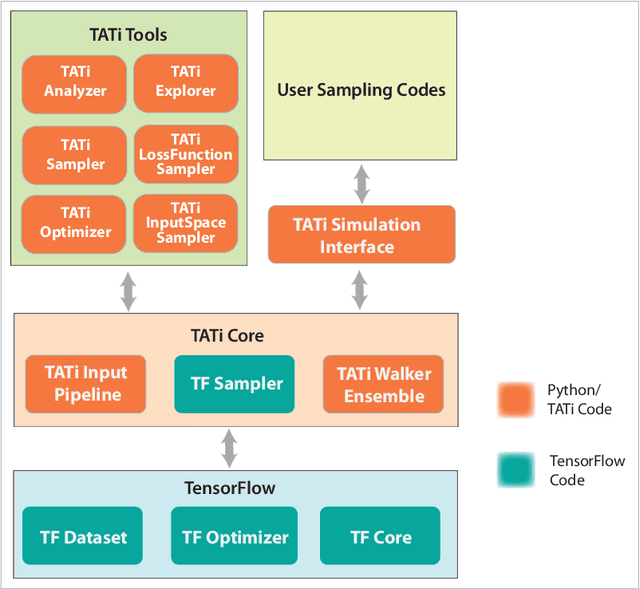
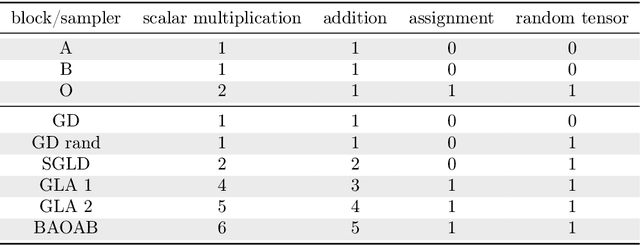
We describe a TensorFlow-based library for posterior sampling and exploration in machine learning applications. TATi, the Thermodynamic Analytics ToolkIt, implements algorithms for 2nd order (underdamped) Langevin dynamics and Hamiltonian Monte Carlo (HMC). It also allows for rapid prototyping of new sampling methods in pure Python and supports an ensemble framework for generating multiple trajectories in parallel, a capability that is demonstrated by the implementation of a recently proposed ensemble preconditioning sampling procedure. In addition to explaining the architecture of TATi and its connections with the TensorFlow framework, this article contains preliminary numerical experiments to explore the efficiency of posterior sampling strategies in ML applications, in comparison to standard training strategies. We provide a glimpse of the potential of the new toolkit by studying (and visualizing) the loss landscape of a neural network applied to the MNIST hand-written digits data set.

Ensemble preconditioning for Markov chain Monte Carlo simulation

We describe parallel Markov chain Monte Carlo methods that propagate a collective ensemble of paths, with local covariance information calculated from neighboring replicas. The use of collective dynamics eliminates multiplicative noise and stabilizes the dynamics thus providing a practical approach to difficult anisotropic sampling problems in high dimensions. Numerical experiments with model problems demonstrate that dramatic potential speedups, compared to various alternative schemes, are attainable.