Improving the stability of the covariance-controlled adaptive Langevin thermostat for large-scale Bayesian sampling

Stochastic gradient Langevin dynamics and its variants approximate the likelihood of an entire dataset, via random (and typically much smaller) subsets, in the setting of Bayesian sampling. Due to the (often substantial) improvement of the computational efficiency, they have been widely used in large-scale machine learning applications. It has been demonstrated that the so-called covariance-controlled adaptive Langevin (CCAdL) thermostat, which incorporates an additional term involving the covariance matrix of the noisy force, outperforms popular alternative methods. A moving average is used in CCAdL to estimate the covariance matrix of the noisy force, in which case the covariance matrix will converge to a constant matrix in long-time limit. Moreover, it appears in our numerical experiments that the use of a moving average could reduce the stability of the numerical integrators, thereby limiting the largest usable stepsize. In this article, we propose a modified CCAdL (i.e., mCCAdL) thermostat that uses the scaling part of the scaling and squaring method together with a truncated Taylor series approximation to the exponential to numerically approximate the exact solution to the subsystem involving the additional term proposed in CCAdL. We also propose a symmetric splitting method for mCCAdL, instead of an Euler-type discretisation used in the original CCAdL thermostat. We demonstrate in our numerical experiments that the newly proposed mCCAdL thermostat achieves a substantial improvement in the numerical stability over the original CCAdL thermostat, while significantly outperforming popular alternative stochastic gradient methods in terms of the numerical accuracy for large-scale machine learning applications.

Covariance-Controlled Adaptive Langevin Thermostat for Large-Scale Bayesian Sampling

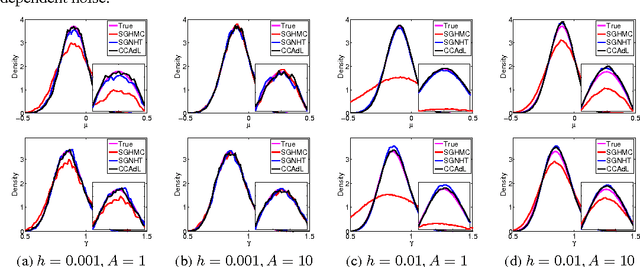
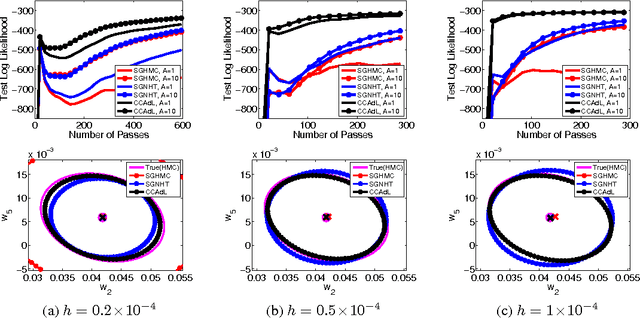
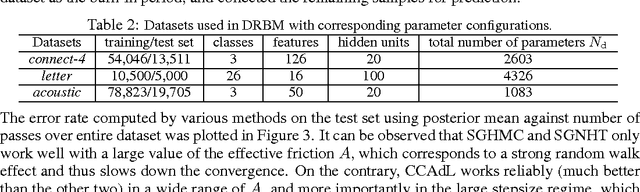
Monte Carlo sampling for Bayesian posterior inference is a common approach used in machine learning. The Markov Chain Monte Carlo procedures that are used are often discrete-time analogues of associated stochastic differential equations (SDEs). These SDEs are guaranteed to leave invariant the required posterior distribution. An area of current research addresses the computational benefits of stochastic gradient methods in this setting. Existing techniques rely on estimating the variance or covariance of the subsampling error, and typically assume constant variance. In this article, we propose a covariance-controlled adaptive Langevin thermostat that can effectively dissipate parameter-dependent noise while maintaining a desired target distribution. The proposed method achieves a substantial speedup over popular alternative schemes for large-scale machine learning applications.