GINN: Geometric Illustration of Neural Networks

This informal technical report details the geometric illustration of decision boundaries for ReLU units in a three layer fully connected neural network. The network is designed and trained to predict pixel intensity from an (x, y) input location. The Geometric Illustration of Neural Networks (GINN) tool was built to visualise and track the points at which ReLU units switch from being active to off (or vice versa) as the network undergoes training. Several phenomenon were observed and are discussed herein. This technical report is a supporting document to the blog post with online demos and is available at http://www.bayeswatch.com/2018/09/17/GINN/.

CINIC-10 is not ImageNet or CIFAR-10

In this brief technical report we introduce the CINIC-10 dataset as a plug-in extended alternative for CIFAR-10. It was compiled by combining CIFAR-10 with images selected and downsampled from the ImageNet database. We present the approach to compiling the dataset, illustrate the example images for different classes, give pixel distributions for each part of the repository, and give some standard benchmarks for well known models. Details for download, usage, and compilation can be found in the associated github repository.

Asymptotically exact inference in differentiable generative models

Many generative models can be expressed as a differentiable function of random inputs drawn from some simple probability density. This framework includes both deep generative architectures such as Variational Autoencoders and a large class of procedurally defined simulator models. We present a method for performing efficient MCMC inference in such models when conditioning on observations of the model output. For some models this offers an asymptotically exact inference method where Approximate Bayesian Computation might otherwise be employed. We use the intuition that inference corresponds to integrating a density across the manifold corresponding to the set of inputs consistent with the observed outputs. This motivates the use of a constrained variant of Hamiltonian Monte Carlo which leverages the smooth geometry of the manifold to coherently move between inputs exactly consistent with observations. We validate the method by performing inference tasks in a diverse set of models.

Stochastic Parallel Block Coordinate Descent for Large-scale Saddle Point Problems

We consider convex-concave saddle point problems with a separable structure and non-strongly convex functions. We propose an efficient stochastic block coordinate descent method using adaptive primal-dual updates, which enables flexible parallel optimization for large-scale problems. Our method shares the efficiency and flexibility of block coordinate descent methods with the simplicity of primal-dual methods and utilizing the structure of the separable convex-concave saddle point problem. It is capable of solving a wide range of machine learning applications, including robust principal component analysis, Lasso, and feature selection by group Lasso, etc. Theoretically and empirically, we demonstrate significantly better performance than state-of-the-art methods in all these applications.

Covariance-Controlled Adaptive Langevin Thermostat for Large-Scale Bayesian Sampling

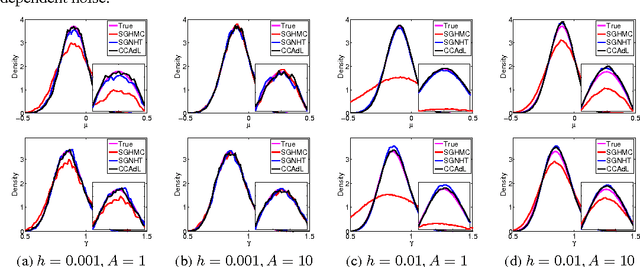
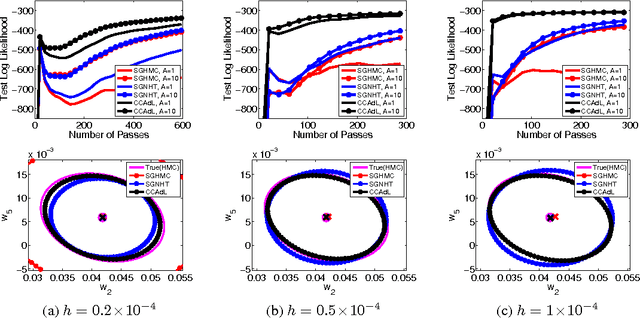
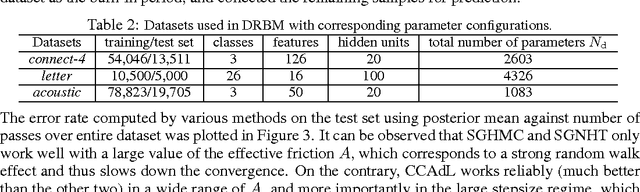
Monte Carlo sampling for Bayesian posterior inference is a common approach used in machine learning. The Markov Chain Monte Carlo procedures that are used are often discrete-time analogues of associated stochastic differential equations (SDEs). These SDEs are guaranteed to leave invariant the required posterior distribution. An area of current research addresses the computational benefits of stochastic gradient methods in this setting. Existing techniques rely on estimating the variance or covariance of the subsampling error, and typically assume constant variance. In this article, we propose a covariance-controlled adaptive Langevin thermostat that can effectively dissipate parameter-dependent noise while maintaining a desired target distribution. The proposed method achieves a substantial speedup over popular alternative schemes for large-scale machine learning applications.

Adaptive Stochastic Primal-Dual Coordinate Descent for Separable Saddle Point Problems

We consider a generic convex-concave saddle point problem with separable structure, a form that covers a wide-ranged machine learning applications. Under this problem structure, we follow the framework of primal-dual updates for saddle point problems, and incorporate stochastic block coordinate descent with adaptive stepsize into this framework. We theoretically show that our proposal of adaptive stepsize potentially achieves a sharper linear convergence rate compared with the existing methods. Additionally, since we can select "mini-batch" of block coordinates to update, our method is also amenable to parallel processing for large-scale data. We apply the proposed method to regularized empirical risk minimization and show that it performs comparably or, more often, better than state-of-the-art methods on both synthetic and real-world data sets.

The supervised hierarchical Dirichlet process

We propose the supervised hierarchical Dirichlet process (sHDP), a nonparametric generative model for the joint distribution of a group of observations and a response variable directly associated with that whole group. We compare the sHDP with another leading method for regression on grouped data, the supervised latent Dirichlet allocation (sLDA) model. We evaluate our method on two real-world classification problems and two real-world regression problems. Bayesian nonparametric regression models based on the Dirichlet process, such as the Dirichlet process-generalised linear models (DP-GLM) have previously been explored; these models allow flexibility in modelling nonlinear relationships. However, until now, Hierarchical Dirichlet Process (HDP) mixtures have not seen significant use in supervised problems with grouped data since a straightforward application of the HDP on the grouped data results in learnt clusters that are not predictive of the responses. The sHDP solves this problem by allowing for clusters to be learnt jointly from the group structure and from the label assigned to each group.

Renewal Strings for Cleaning Astronomical Databases

Large astronomical databases obtained from sky surveys such as the SuperCOSMOS Sky Surveys (SSS) invariably suffer from a small number of spurious records coming from artefactual effects of the telescope, satellites and junk objects in orbit around earth and physical defects on the photographic plate or CCD. Though relatively small in number these spurious records present a significant problem in many situations where they can become a large proportion of the records potentially of interest to a given astronomer. In this paper we focus on the four most common causes of unwanted records in the SSS: satellite or aeroplane tracks, scratches fibres and other linear phenomena introduced to the plate, circular halos around bright stars due to internal reflections within the telescope and diffraction spikes near to bright stars. Accurate and robust techniques are needed for locating and flagging such spurious objects. We have developed renewal strings, a probabilistic technique combining the Hough transform, renewal processes and hidden Markov models which have proven highly effective in this context. The methods are applied to the SSS data to develop a dataset of spurious object detections, along with confidence measures, which can allow this unwanted data to be removed from consideration. These methods are general and can be adapted to any future astronomical survey data.

Dynamic Trees: A Structured Variational Method Giving Efficient Propagation Rules

Dynamic trees are mixtures of tree structured belief networks. They solve some of the problems of fixed tree networks at the cost of making exact inference intractable. For this reason approximate methods such as sampling or mean field approaches have been used. However, mean field approximations assume a factorized distribution over node states. Such a distribution seems unlickely in the posterior, as nodes are highly correlated in the prior. Here a structured variational approach is used, where the posterior distribution over the non-evidential nodes is itself approximated by a dynamic tree. It turns out that this form can be used tractably and efficiently. The result is a set of update rules which can propagate information through the network to obtain both a full variational approximation, and the relevant marginals. The progagtion rules are more efficient than the mean field approach and give noticeable quantitative and qualitative improvement in the inference. The marginals calculated give better approximations to the posterior than loopy propagation on a small toy problem.