Normalization Layers Are All That Sharpness-Aware Minimization Needs

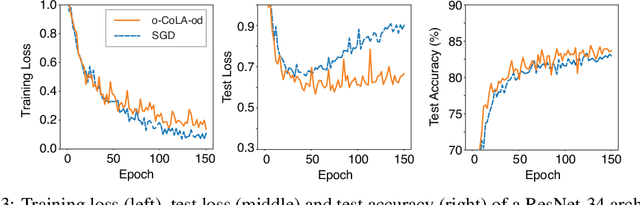
Sharpness-aware minimization (SAM) was proposed to reduce sharpness of minima and has been shown to enhance generalization performance in various settings. In this work we show that perturbing only the affine normalization parameters (comprising less than 0.1% of the total parameters) in the adversarial step of SAM outperforms perturbing all of the parameters. This finding generalizes to different SAM variants and both ResNet (Batch Normalization) and Vision Transformer (Layer Normalization) architectures. We consider alternative sparse perturbation approaches and find that these do not achieve similar performance enhancement at such extreme sparsity levels, showing that this behaviour is unique to the normalization layers. Although our findings reaffirm the effectiveness of SAM in improving generalization performance, they cast doubt on whether this is solely caused by reduced sharpness. The code for our experiments is publicly available at https://github.com/mueller-mp/SAM-ON.

What can linear interpolation of neural network loss landscapes tell us?

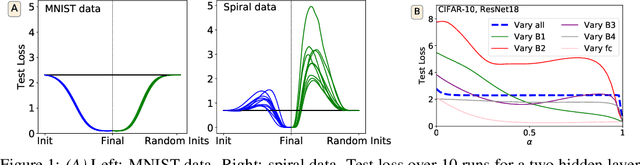
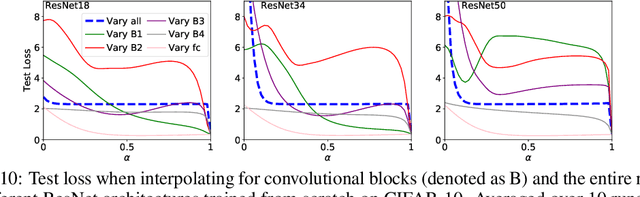
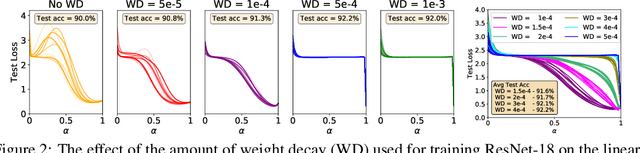
Studying neural network loss landscapes provides insights into the nature of the underlying optimization problems. Unfortunately, loss landscapes are notoriously difficult to visualize in a human-comprehensible fashion. One common way to address this problem is to plot linear slices of the landscape, for example from the initial state of the network to the final state after optimization. On the basis of this analysis, prior work has drawn broader conclusions about the difficulty of the optimization problem. In this paper, we put inferences of this kind to the test, systematically evaluating how linear interpolation and final performance vary when altering the data, choice of initialization, and other optimizer and architecture design choices. Further, we use linear interpolation to study the role played by individual layers and substructures of the network. We find that certain layers are more sensitive to the choice of initialization and optimizer hyperparameter settings, and we exploit these observations to design custom optimization schemes. However, our results cast doubt on the broader intuition that the presence or absence of barriers when interpolating necessarily relates to the success of optimization.

Multirate Training of Neural Networks

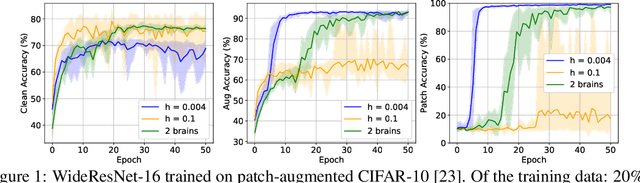
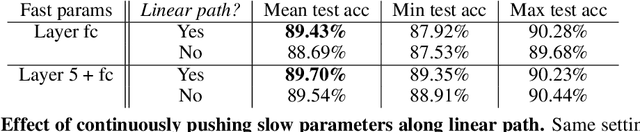
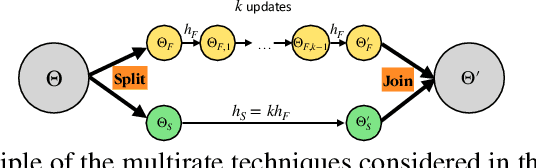
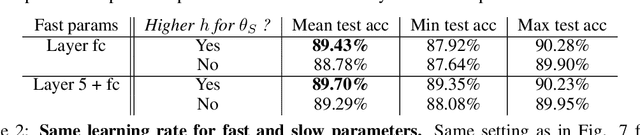
We propose multirate training of neural networks: partitioning neural network parameters into "fast" and "slow" parts which are trained simultaneously using different learning rates. By choosing appropriate partitionings we can obtain large computational speed-ups for transfer learning tasks. We show that for various transfer learning applications in vision and NLP we can fine-tune deep neural networks in almost half the time, without reducing the generalization performance of the resulting model. We also discuss other splitting choices for the neural network parameters which are beneficial in enhancing generalization performance in settings where neural networks are trained from scratch. Finally, we propose an additional multirate technique which can learn different features present in the data by training the full network on different time scales simultaneously. The benefits of using this approach are illustrated for ResNet architectures on image data. Our paper unlocks the potential of using multirate techniques for neural network training and provides many starting points for future work in this area.

Better Training using Weight-Constrained Stochastic Dynamics

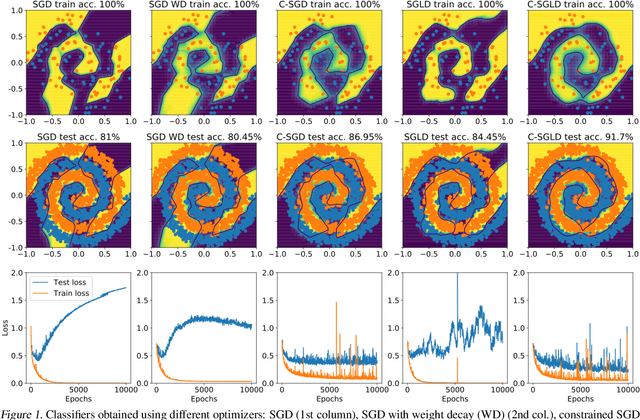
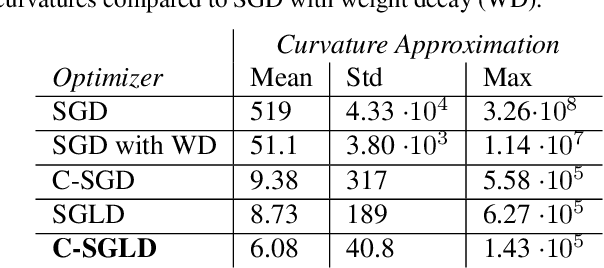
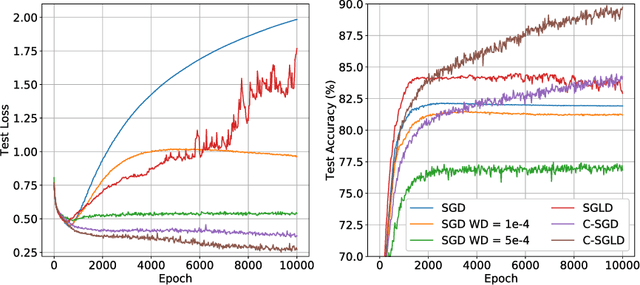
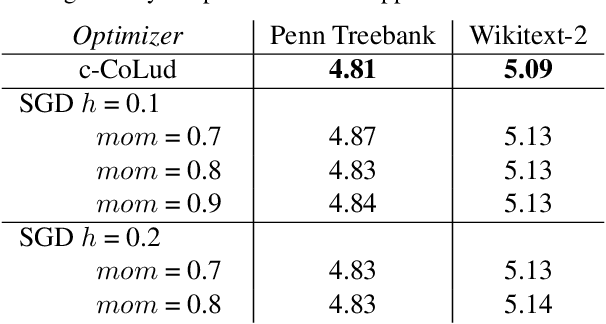
We employ constraints to control the parameter space of deep neural networks throughout training. The use of customized, appropriately designed constraints can reduce the vanishing/exploding gradients problem, improve smoothness of classification boundaries, control weight magnitudes and stabilize deep neural networks, and thus enhance the robustness of training algorithms and the generalization capabilities of neural networks. We provide a general approach to efficiently incorporate constraints into a stochastic gradient Langevin framework, allowing enhanced exploration of the loss landscape. We also present specific examples of constrained training methods motivated by orthogonality preservation for weight matrices and explicit weight normalizations. Discretization schemes are provided both for the overdamped formulation of Langevin dynamics and the underdamped form, in which momenta further improve sampling efficiency. These optimization schemes can be used directly, without needing to adapt neural network architecture design choices or to modify the objective with regularization terms, and see performance improvements in classification tasks.

Constraint-Based Regularization of Neural Networks

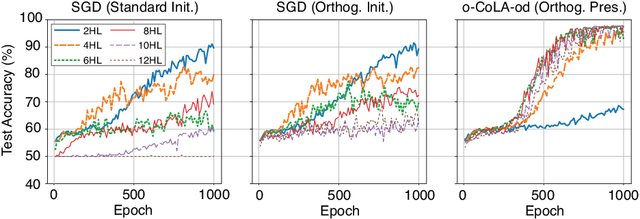
We propose a method for efficiently incorporating constraints into a stochastic gradient Langevin framework for the training of deep neural networks. Constraints allow direct control of the parameter space of the model. Appropriately designed, they reduce the vanishing/exploding gradient problem, control weight magnitudes and stabilize deep neural networks and thus improve the robustness of training algorithms and the generalization capabilities of the trained neural network. We present examples of constrained training methods motivated by orthogonality preservation for weight matrices and explicit weight normalizations. We describe the methods in the overdamped formulation of Langevin dynamics and the underdamped form, in which momenta help to improve sampling efficiency. The methods are explored in test examples in image classification and natural language processing.

Partitioned integrators for thermodynamic parameterization of neural networks

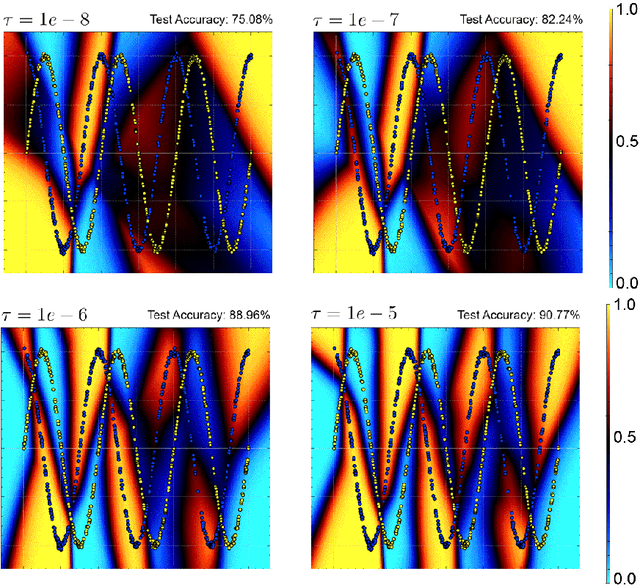
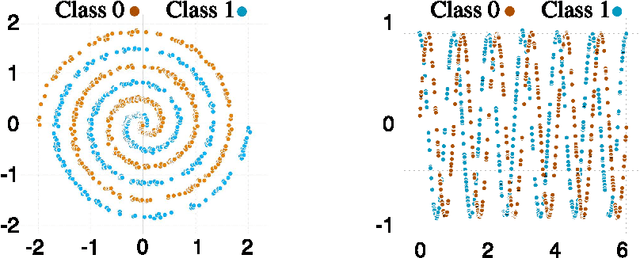
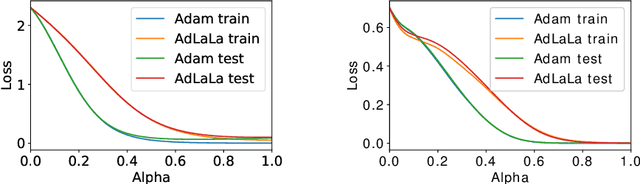
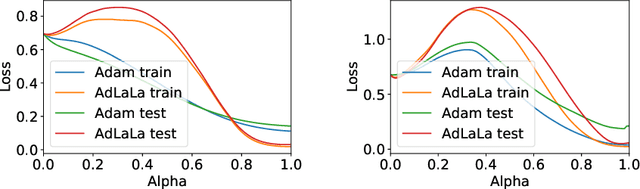
Stochastic Gradient Langevin Dynamics, the "unadjusted Langevin algorithm", and Adaptive Langevin Dynamics (also known as Stochastic Gradient Nos\'{e}-Hoover dynamics) are examples of existing thermodynamic parameterization methods in use for machine learning, but these can be substantially improved. We find that by partitioning the parameters based on natural layer structure we obtain schemes with rapid convergence for data sets with complicated loss landscapes. We describe easy-to-implement hybrid partitioned numerical algorithms, based on discretized stochastic differential equations, which are adapted to feed-forward neural networks, including LaLa (a multi-layer Langevin algorithm), AdLaLa (combining the adaptive Langevin and Langevin algorithms) and LOL (combining Langevin and Overdamped Langevin); we examine the convergence of these methods using numerical studies and compare their performance among themselves and in relation to standard alternatives such as stochastic gradient descent and ADAM. We present evidence that thermodynamic parameterization methods can be (i) faster, (ii) more accurate, and (iii) more robust than standard algorithms incorporated into machine learning frameworks, in particular for data sets with complicated loss landscapes. Moreover, we show in numerical studies that methods based on sampling excite many degrees of freedom. The equipartition property, which is a consequence of their ergodicity, means that these methods keep in play an ensemble of low-loss states during the training process. By drawing parameter states from a sufficiently rich distribution of nearby candidate states, we show that the thermodynamic schemes produce smoother classifiers, improve generalization and reduce overfitting compared to traditional optimizers.