LoGex: Improved tail detection of extremely rare histopathology classes via guided diffusion

In realistic medical settings, the data are often inherently long-tailed, with most samples concentrated in a few classes and a long tail of rare classes, usually containing just a few samples. This distribution presents a significant challenge because rare conditions are critical to detect and difficult to classify due to limited data. In this paper, rather than attempting to classify rare classes, we aim to detect these as out-of-distribution data reliably. We leverage low-rank adaption (LoRA) and diffusion guidance to generate targeted synthetic data for the detection problem. We significantly improve the OOD detection performance on a challenging histopathological task with only ten samples per tail class without losing classification accuracy on the head classes.

Normalization Layers Are All That Sharpness-Aware Minimization Needs

Sharpness-aware minimization (SAM) was proposed to reduce sharpness of minima and has been shown to enhance generalization performance in various settings. In this work we show that perturbing only the affine normalization parameters (comprising less than 0.1% of the total parameters) in the adversarial step of SAM outperforms perturbing all of the parameters. This finding generalizes to different SAM variants and both ResNet (Batch Normalization) and Vision Transformer (Layer Normalization) architectures. We consider alternative sparse perturbation approaches and find that these do not achieve similar performance enhancement at such extreme sparsity levels, showing that this behaviour is unique to the normalization layers. Although our findings reaffirm the effectiveness of SAM in improving generalization performance, they cast doubt on whether this is solely caused by reduced sharpness. The code for our experiments is publicly available at https://github.com/mueller-mp/SAM-ON.

Leveraging Stochastic Predictions of Bayesian Neural Networks for Fluid Simulations

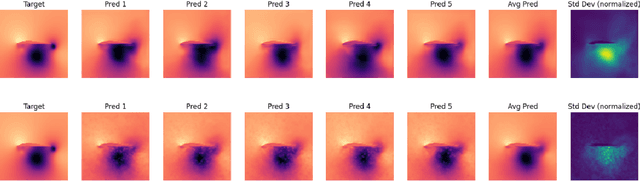
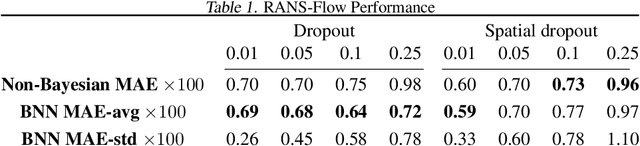
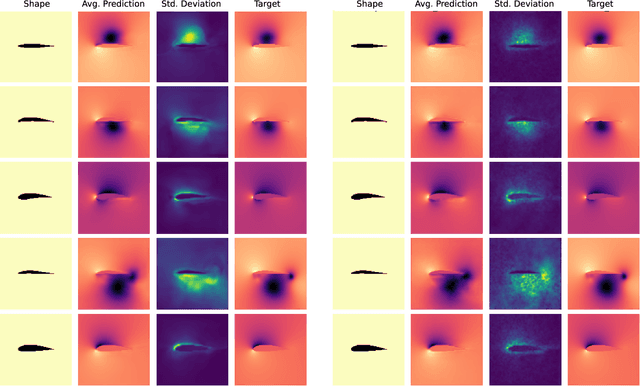
We investigate uncertainty estimation and multimodality via the non-deterministic predictions of Bayesian neural networks (BNNs) in fluid simulations. To this end, we deploy BNNs in three challenging experimental test-cases of increasing complexity: We show that BNNs, when used as surrogate models for steady-state fluid flow predictions, provide accurate physical predictions together with sensible estimates of uncertainty. Further, we experiment with perturbed temporal sequences from Navier-Stokes simulations and evaluate the capabilities of BNNs to capture multimodal evolutions. While our findings indicate that this is problematic for large perturbations, our results show that the networks learn to correctly predict high uncertainties in such situations. Finally, we study BNNs in the context of solver interactions with turbulent plasma flows. We find that BNN-based corrector networks can stabilize coarse-grained simulations and successfully create multimodal trajectories.

Physics-based Deep Learning

This digital book contains a practical and comprehensive introduction of everything related to deep learning in the context of physical simulations. As much as possible, all topics come with hands-on code examples in the form of Jupyter notebooks to quickly get started. Beyond standard supervised learning from data, we'll look at physical loss constraints, more tightly coupled learning algorithms with differentiable simulations, as well as reinforcement learning and uncertainty modeling. We live in exciting times: these methods have a huge potential to fundamentally change what computer simulations can achieve.