Exploring Physical Latent Spaces for Deep Learning

We explore training deep neural network models in conjunction with physical simulations via partial differential equations (PDEs), using the simulated degrees of freedom as latent space for the neural network. In contrast to previous work, we do not impose constraints on the simulated space, but rather treat its degrees of freedom purely as tools to be used by the neural network. We demonstrate this concept for learning reduced representations. It is typically extremely challenging for conventional simulations to faithfully preserve the correct solutions over long time-spans with traditional, reduced representations. This problem is particularly pronounced for solutions with large amounts of small scale features. Here, data-driven methods can learn to restore the details as required for accurate solutions of the underlying PDE problem. We explore the use of physical, reduced latent space within this context, and train models such that they can modify the content of physical states as much as needed to best satisfy the learning objective. Surprisingly, this autonomy allows the neural network to discover alternate dynamics that enable a significantly improved performance in the given tasks. We demonstrate this concept for a range of challenging test cases, among others, for Navier-Stokes based turbulence simulations.

Physics-based Deep Learning

This digital book contains a practical and comprehensive introduction of everything related to deep learning in the context of physical simulations. As much as possible, all topics come with hands-on code examples in the form of Jupyter notebooks to quickly get started. Beyond standard supervised learning from data, we'll look at physical loss constraints, more tightly coupled learning algorithms with differentiable simulations, as well as reinforcement learning and uncertainty modeling. We live in exciting times: these methods have a huge potential to fundamentally change what computer simulations can achieve.

ScalarFlow: A Large-Scale Volumetric Data Set of Real-world Scalar Transport Flows for Computer Animation and Machine Learning

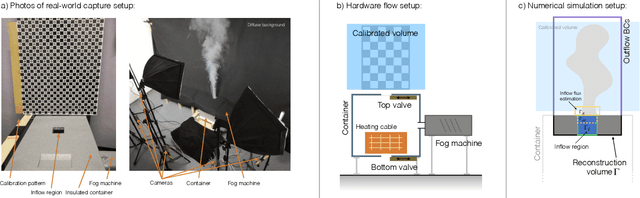
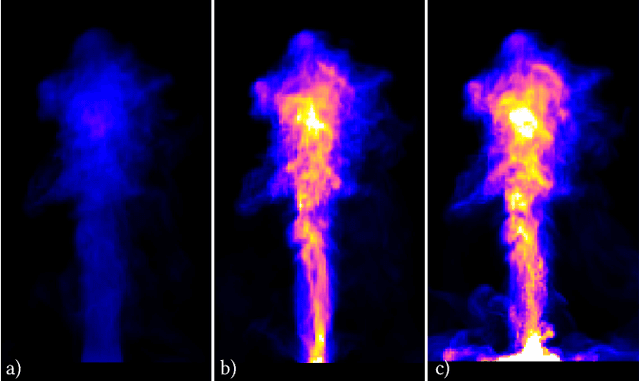
In this paper, we present ScalarFlow, a first large-scale data set of reconstructions of real-world smoke plumes. We additionally propose a framework for accurate physics-based reconstructions from a small number of video streams. Central components of our algorithm are a novel estimation of unseen inflow regions and an efficient regularization scheme. Our data set includes a large number of complex and natural buoyancy-driven flows. The flows transition to turbulent flows and contain observable scalar transport processes. As such, the ScalarFlow data set is tailored towards computer graphics, vision, and learning applications. The published data set will contain volumetric reconstructions of velocity and density, input image sequences, together with calibration data, code, and instructions how to recreate the commodity hardware capture setup. We further demonstrate one of the many potential application areas: a first perceptual evaluation study, which reveals that the complexity of the captured flows requires a huge simulation resolution for regular solvers in order to recreate at least parts of the natural complexity contained in the captured data.

Solver-in-the-Loop: Learning from Differentiable Physics to Interact with Iterative PDE-Solvers

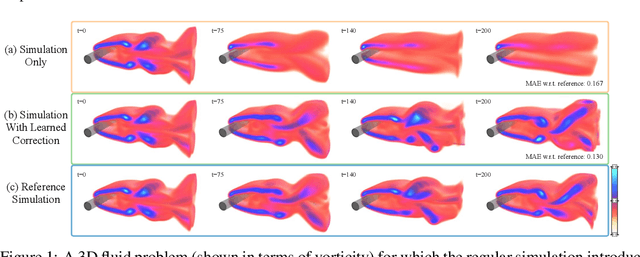
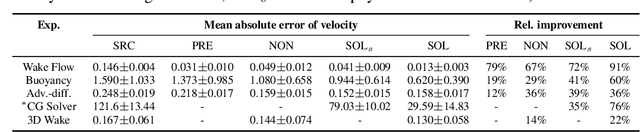
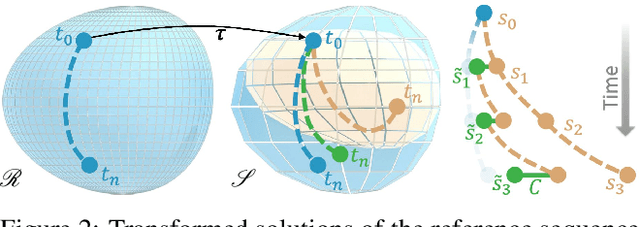
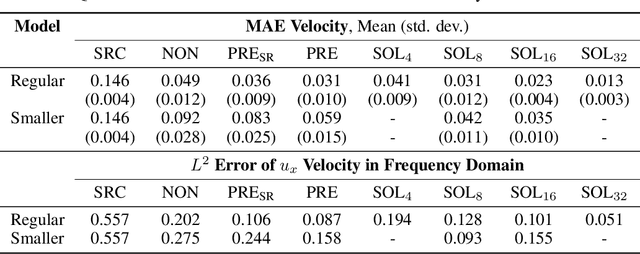
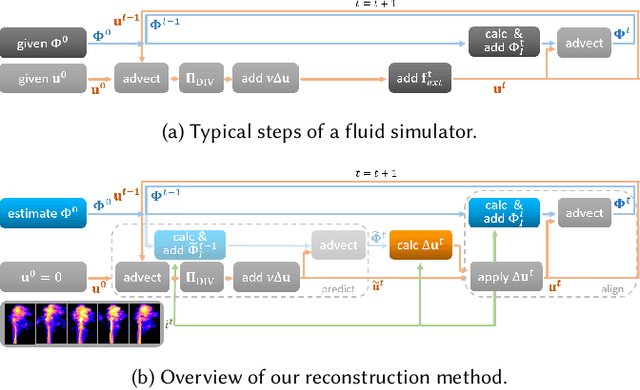
Finding accurate solutions to partial differential equations (PDEs) is a crucial task in all scientific and engineering disciplines. It has recently been shown that machine learning methods can improve the solution accuracy by correcting for effects not captured by the discretized PDE. We target the problem of reducing numerical errors of iterative PDE solvers and compare different learning approaches for finding complex correction functions. We find that previously used learning approaches are significantly outperformed by methods that integrate the solver into the training loop and thereby allow the model to interact with the PDE during training. This provides the model with realistic input distributions that take previous corrections into account, yielding improvements in accuracy with stable rollouts of several hundred recurrent evaluation steps and surpassing even tailored supervised variants. We highlight the performance of the differentiable physics networks for a wide variety of PDEs, from non-linear advection-diffusion systems to three-dimensional Navier-Stokes flows.

Learning Similarity Metrics for Numerical Simulations

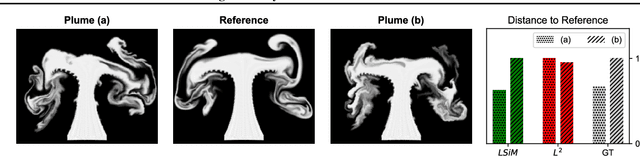
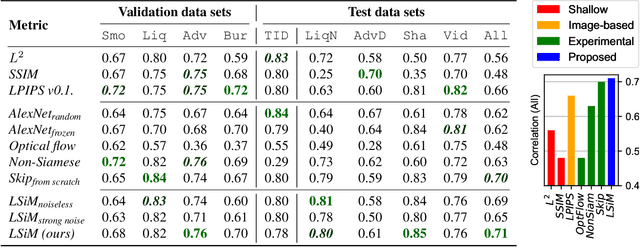
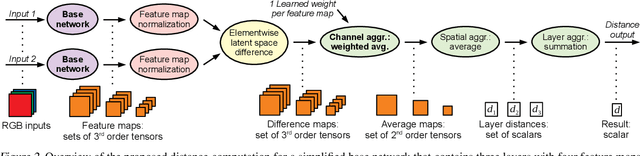
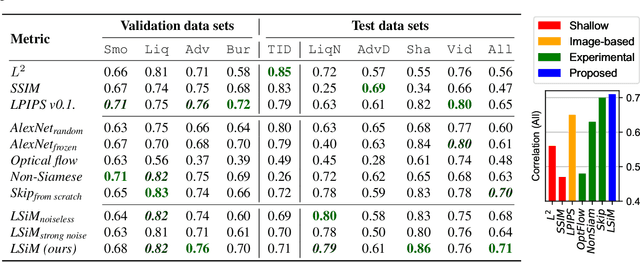
We propose a neural network-based approach that computes a stable and generalizing metric (LSiM), to compare field data from a variety of numerical simulation sources. Our method employs a Siamese network architecture that is motivated by the mathematical properties of a metric. We leverage a controllable data generation setup with partial differential equation (PDE) solvers to create increasingly different outputs from a reference simulation in a controlled environment. A central component of our learned metric is a specialized loss function that introduces knowledge about the correlation between single data samples into the training process. To demonstrate that the proposed approach outperforms existing simple metrics for vector spaces and other learned, image-based metrics, we evaluate the different methods on a large range of test data. Additionally, we analyze benefits for generalization and the impact of an adjustable training data difficulty. The robustness of LSiM is demonstrated via an evaluation on three real-world data sets.