Learning Similarity Metrics for Numerical Simulations

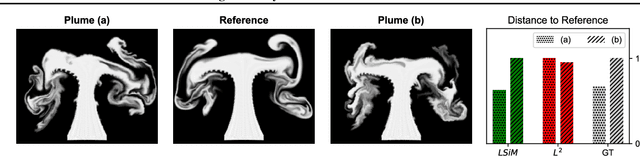
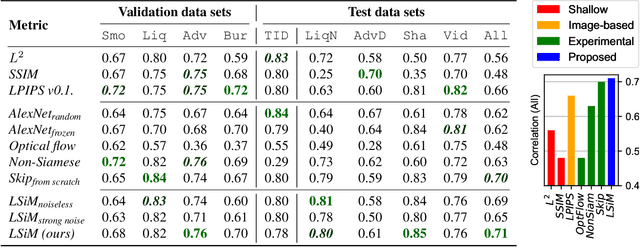
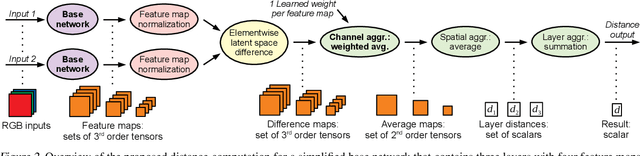
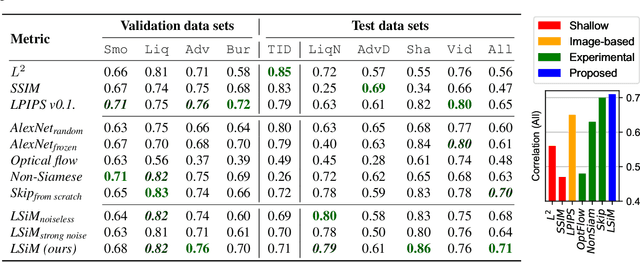
We propose a neural network-based approach that computes a stable and generalizing metric (LSiM), to compare field data from a variety of numerical simulation sources. Our method employs a Siamese network architecture that is motivated by the mathematical properties of a metric. We leverage a controllable data generation setup with partial differential equation (PDE) solvers to create increasingly different outputs from a reference simulation in a controlled environment. A central component of our learned metric is a specialized loss function that introduces knowledge about the correlation between single data samples into the training process. To demonstrate that the proposed approach outperforms existing simple metrics for vector spaces and other learned, image-based metrics, we evaluate the different methods on a large range of test data. Additionally, we analyze benefits for generalization and the impact of an adjustable training data difficulty. The robustness of LSiM is demonstrated via an evaluation on three real-world data sets.