Turbulent Flow Simulation using Autoregressive Conditional Diffusion Models

Simulating turbulent flows is crucial for a wide range of applications, and machine learning-based solvers are gaining increasing relevance. However, achieving stability when generalizing to longer rollout horizons remains a persistent challenge for learned PDE solvers. We address this challenge by introducing a fully data-driven fluid solver that utilizes an autoregressive rollout based on conditional diffusion models. We show that this approach offers clear advantages in terms of rollout stability compared to other learned baselines. Remarkably, these improvements in stability are achieved without compromising the quality of generated samples, and our model successfully generalizes to flow parameters beyond the training regime. Additionally, the probabilistic nature of the diffusion approach allows for inferring predictions that align with the statistics of the underlying physics. We quantitatively and qualitatively evaluate the performance of our method on a range of challenging scenarios, including incompressible and transonic flows, as well as isotropic turbulence.

Learning Similarity Metrics for Volumetric Simulations with Multiscale CNNs

Simulations that produce three-dimensional data are ubiquitous in science, ranging from fluid flows to plasma physics. We propose a similarity model based on entropy, which allows for the creation of physically meaningful ground truth distances for the similarity assessment of scalar and vectorial data, produced from transport and motion-based simulations. Utilizing two data acquisition methods derived from this model, we create collections of fields from numerical PDE solvers and existing simulation data repositories, and highlight the importance of an appropriate data distribution for an effective training process. Furthermore, a multiscale CNN architecture that computes a volumetric similarity metric (VolSiM) is proposed. To the best of our knowledge this is the first learning method inherently designed to address the challenges arising for the similarity assessment of high-dimensional simulation data. Additionally, the tradeoff between a large batch size and an accurate correlation computation for correlation-based loss functions is investigated, and the metric's invariance with respect to rotation and scale operations is analyzed. Finally, the robustness and generalization of VolSiM is evaluated on a large range of test data, as well as a particularly challenging turbulence case study, that is close to potential real-world applications.

Learning Similarity Metrics for Numerical Simulations

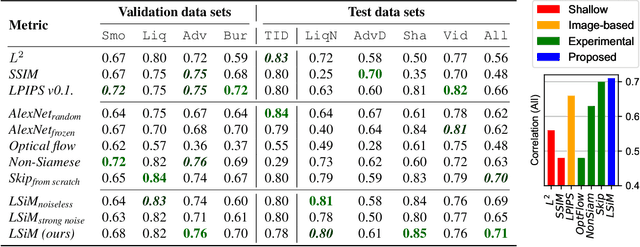
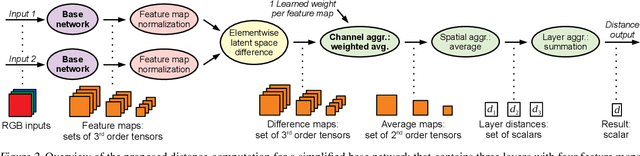
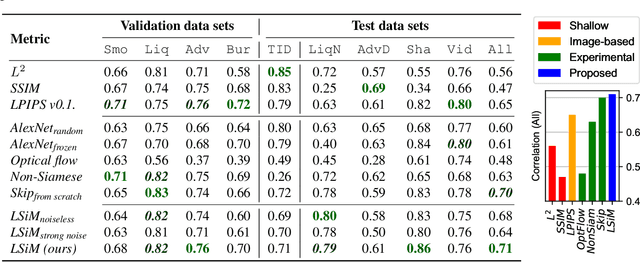
We propose a neural network-based approach that computes a stable and generalizing metric (LSiM), to compare field data from a variety of numerical simulation sources. Our method employs a Siamese network architecture that is motivated by the mathematical properties of a metric. We leverage a controllable data generation setup with partial differential equation (PDE) solvers to create increasingly different outputs from a reference simulation in a controlled environment. A central component of our learned metric is a specialized loss function that introduces knowledge about the correlation between single data samples into the training process. To demonstrate that the proposed approach outperforms existing simple metrics for vector spaces and other learned, image-based metrics, we evaluate the different methods on a large range of test data. Additionally, we analyze benefits for generalization and the impact of an adjustable training data difficulty. The robustness of LSiM is demonstrated via an evaluation on three real-world data sets.