The Unreasonable Effectiveness of Solving Inverse Problems with Neural Networks

Finding model parameters from data is an essential task in science and engineering, from weather and climate forecasts to plasma control. Previous works have employed neural networks to greatly accelerate finding solutions to inverse problems. Of particular interest are end-to-end models which utilize differentiable simulations in order to backpropagate feedback from the simulated process to the network weights and enable roll-out of multiple time steps. So far, it has been assumed that, while model inference is faster than classical optimization, this comes at the cost of a decrease in solution accuracy. We show that this is generally not true. In fact, neural networks trained to learn solutions to inverse problems can find better solutions than classical optimizers even on their training set. To demonstrate this, we perform both a theoretical analysis as well an extensive empirical evaluation on challenging problems involving local minima, chaos, and zero-gradient regions. Our findings suggest an alternative use for neural networks: rather than generalizing to new data for fast inference, they can also be used to find better solutions on known data.

Half-Inverse Gradients for Physical Deep Learning

Recent works in deep learning have shown that integrating differentiable physics simulators into the training process can greatly improve the quality of results. Although this combination represents a more complex optimization task than supervised neural network training, the same gradient-based optimizers are typically employed to minimize the loss function. However, the integrated physics solvers have a profound effect on the gradient flow as manipulating scales in magnitude and direction is an inherent property of many physical processes. Consequently, the gradient flow is often highly unbalanced and creates an environment in which existing gradient-based optimizers perform poorly. In this work, we analyze the characteristics of both physical and neural network optimizations to derive a new method that does not suffer from this phenomenon. Our method is based on a half-inversion of the Jacobian and combines principles of both classical network and physics optimizers to solve the combined optimization task. Compared to state-of-the-art neural network optimizers, our method converges more quickly and yields better solutions, which we demonstrate on three complex learning problems involving nonlinear oscillators, the Schroedinger equation and the Poisson problem.

Simulating Liquids with Graph Networks

Simulating complex dynamics like fluids with traditional simulators is computationally challenging. Deep learning models have been proposed as an efficient alternative, extending or replacing parts of traditional simulators. We investigate graph neural networks (GNNs) for learning fluid dynamics and find that their generalization capability is more limited than previous works would suggest. We also challenge the current practice of adding random noise to the network inputs in order to improve its generalization capability and simulation stability. We find that inserting the real data distribution, e.g. by unrolling multiple simulation steps, improves accuracy and that hiding all domain-specific features from the learning model improves generalization. Our results indicate that learning models, such as GNNs, fail to learn the exact underlying dynamics unless the training set is devoid of any other problem-specific correlations that could be used as shortcuts.

Physical Gradients for Deep Learning

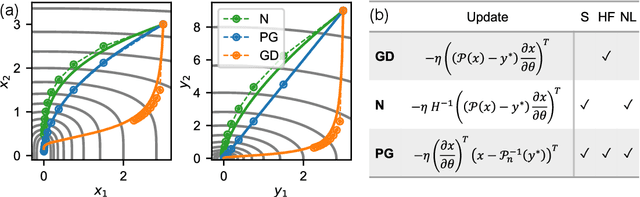
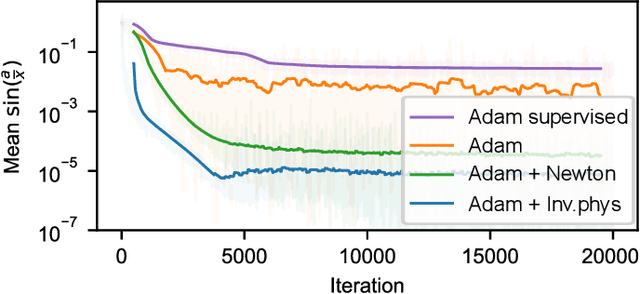
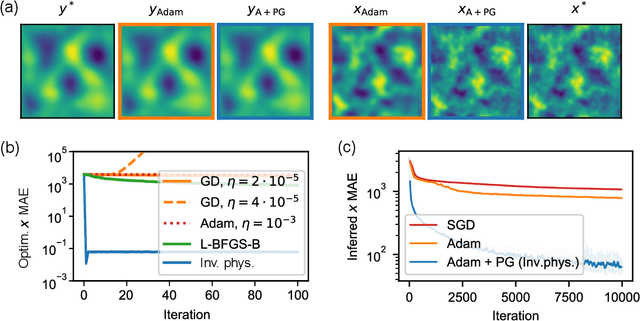
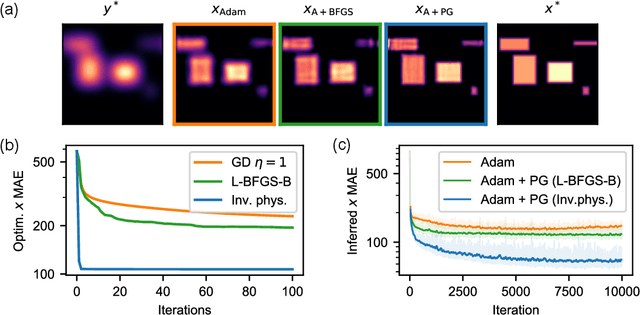
Solving inverse problems, such as parameter estimation and optimal control, is a vital part of science. Many experiments repeatedly collect data and employ machine learning algorithms to quickly infer solutions to the associated inverse problems. We find that state-of-the-art training techniques are not well-suited to many problems that involve physical processes since the magnitude and direction of the gradients can vary strongly. We propose a novel hybrid training approach that combines higher-order optimization methods with machine learning techniques. We replace the gradient of the physical process by a new construct, referred to as the physical gradient. This also allows us to introduce domain knowledge into training by incorporating priors about the solution space into the gradients. We demonstrate the capabilities of our method on a variety of canonical physical systems, showing that physical gradients yield significant improvements on a wide range of optimization and learning problems.

Physics-based Deep Learning

This digital book contains a practical and comprehensive introduction of everything related to deep learning in the context of physical simulations. As much as possible, all topics come with hands-on code examples in the form of Jupyter notebooks to quickly get started. Beyond standard supervised learning from data, we'll look at physical loss constraints, more tightly coupled learning algorithms with differentiable simulations, as well as reinforcement learning and uncertainty modeling. We live in exciting times: these methods have a huge potential to fundamentally change what computer simulations can achieve.

Solver-in-the-Loop: Learning from Differentiable Physics to Interact with Iterative PDE-Solvers

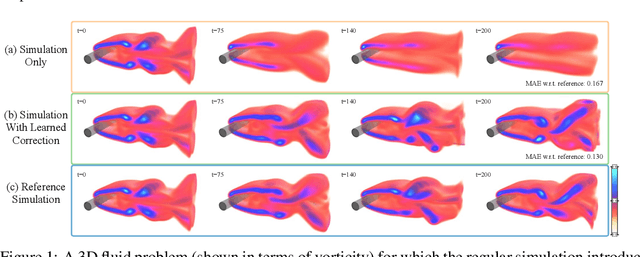
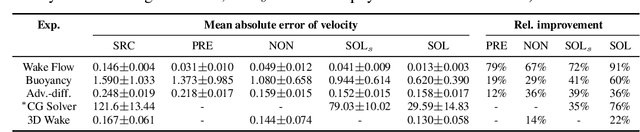
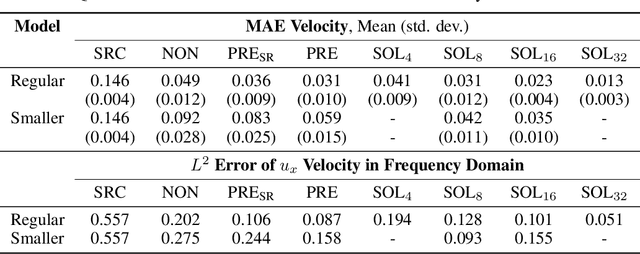
Finding accurate solutions to partial differential equations (PDEs) is a crucial task in all scientific and engineering disciplines. It has recently been shown that machine learning methods can improve the solution accuracy by correcting for effects not captured by the discretized PDE. We target the problem of reducing numerical errors of iterative PDE solvers and compare different learning approaches for finding complex correction functions. We find that previously used learning approaches are significantly outperformed by methods that integrate the solver into the training loop and thereby allow the model to interact with the PDE during training. This provides the model with realistic input distributions that take previous corrections into account, yielding improvements in accuracy with stable rollouts of several hundred recurrent evaluation steps and surpassing even tailored supervised variants. We highlight the performance of the differentiable physics networks for a wide variety of PDEs, from non-linear advection-diffusion systems to three-dimensional Navier-Stokes flows.

Learning to Control PDEs with Differentiable Physics

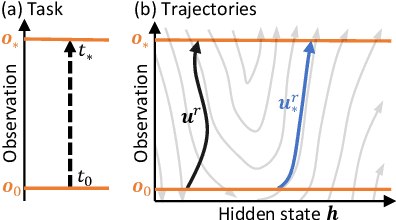
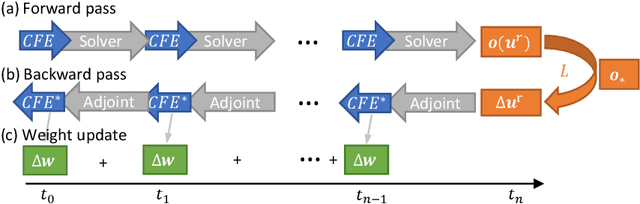
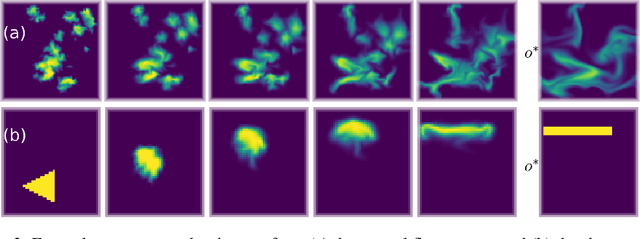
Predicting outcomes and planning interactions with the physical world are long-standing goals for machine learning. A variety of such tasks involves continuous physical systems, which can be described by partial differential equations (PDEs) with many degrees of freedom. Existing methods that aim to control the dynamics of such systems are typically limited to relatively short time frames or a small number of interaction parameters. We present a novel hierarchical predictor-corrector scheme which enables neural networks to learn to understand and control complex nonlinear physical systems over long time frames. We propose to split the problem into two distinct tasks: planning and control. To this end, we introduce a predictor network that plans optimal trajectories and a control network that infers the corresponding control parameters. Both stages are trained end-to-end using a differentiable PDE solver. We demonstrate that our method successfully develops an understanding of complex physical systems and learns to control them for tasks involving PDEs such as the incompressible Navier-Stokes equations.