Physical Gradients for Deep Learning

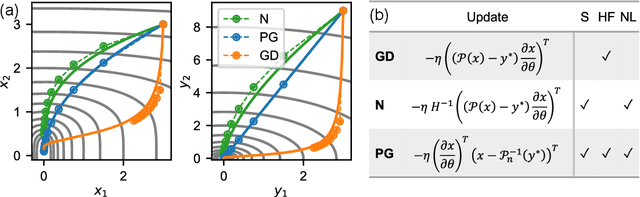
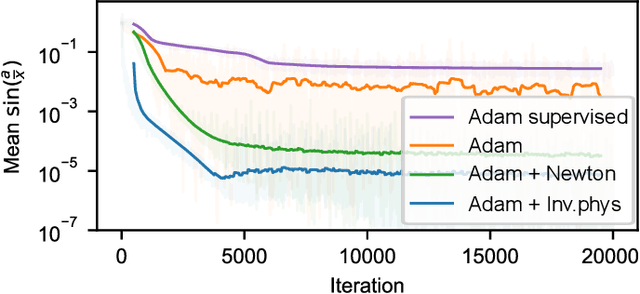
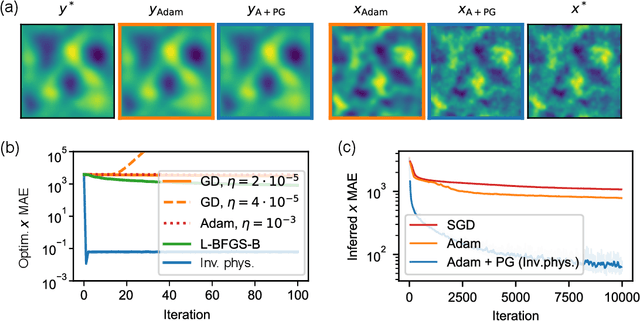
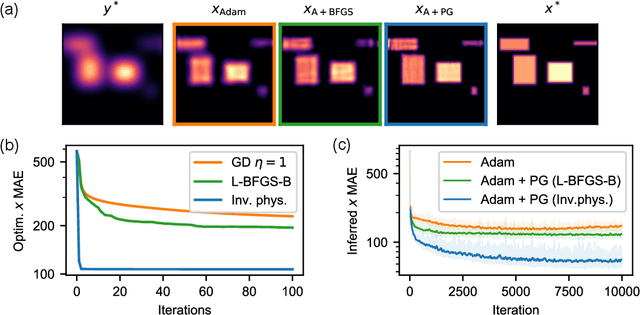
Solving inverse problems, such as parameter estimation and optimal control, is a vital part of science. Many experiments repeatedly collect data and employ machine learning algorithms to quickly infer solutions to the associated inverse problems. We find that state-of-the-art training techniques are not well-suited to many problems that involve physical processes since the magnitude and direction of the gradients can vary strongly. We propose a novel hybrid training approach that combines higher-order optimization methods with machine learning techniques. We replace the gradient of the physical process by a new construct, referred to as the physical gradient. This also allows us to introduce domain knowledge into training by incorporating priors about the solution space into the gradients. We demonstrate the capabilities of our method on a variety of canonical physical systems, showing that physical gradients yield significant improvements on a wide range of optimization and learning problems.