Stabilizing Backpropagation Through Time to Learn Complex Physics

Of all the vector fields surrounding the minima of recurrent learning setups, the gradient field with its exploding and vanishing updates appears a poor choice for optimization, offering little beyond efficient computability. We seek to improve this suboptimal practice in the context of physics simulations, where backpropagating feedback through many unrolled time steps is considered crucial to acquiring temporally coherent behavior. The alternative vector field we propose follows from two principles: physics simulators, unlike neural networks, have a balanced gradient flow, and certain modifications to the backpropagation pass leave the positions of the original minima unchanged. As any modification of backpropagation decouples forward and backward pass, the rotation-free character of the gradient field is lost. Therefore, we discuss the negative implications of using such a rotational vector field for optimization and how to counteract them. Our final procedure is easily implementable via a sequence of gradient stopping and component-wise comparison operations, which do not negatively affect scalability. Our experiments on three control problems show that especially as we increase the complexity of each task, the unbalanced updates from the gradient can no longer provide the precise control signals necessary while our method still solves the tasks. Our code can be found at https://github.com/tum-pbs/StableBPTT.

Half-Inverse Gradients for Physical Deep Learning

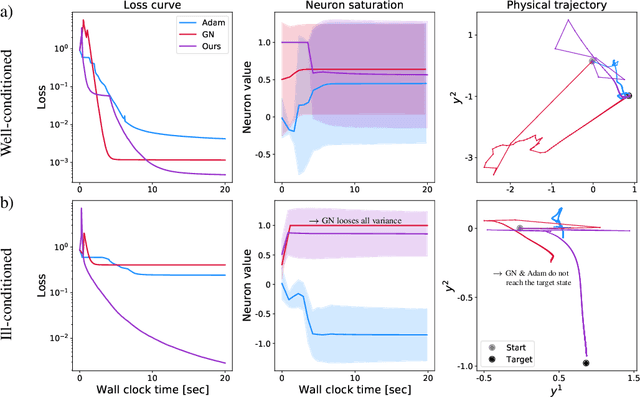
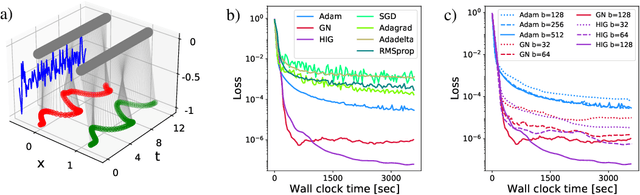
Recent works in deep learning have shown that integrating differentiable physics simulators into the training process can greatly improve the quality of results. Although this combination represents a more complex optimization task than supervised neural network training, the same gradient-based optimizers are typically employed to minimize the loss function. However, the integrated physics solvers have a profound effect on the gradient flow as manipulating scales in magnitude and direction is an inherent property of many physical processes. Consequently, the gradient flow is often highly unbalanced and creates an environment in which existing gradient-based optimizers perform poorly. In this work, we analyze the characteristics of both physical and neural network optimizations to derive a new method that does not suffer from this phenomenon. Our method is based on a half-inversion of the Jacobian and combines principles of both classical network and physics optimizers to solve the combined optimization task. Compared to state-of-the-art neural network optimizers, our method converges more quickly and yields better solutions, which we demonstrate on three complex learning problems involving nonlinear oscillators, the Schroedinger equation and the Poisson problem.

Physics-based Deep Learning

This digital book contains a practical and comprehensive introduction of everything related to deep learning in the context of physical simulations. As much as possible, all topics come with hands-on code examples in the form of Jupyter notebooks to quickly get started. Beyond standard supervised learning from data, we'll look at physical loss constraints, more tightly coupled learning algorithms with differentiable simulations, as well as reinforcement learning and uncertainty modeling. We live in exciting times: these methods have a huge potential to fundamentally change what computer simulations can achieve.