Multimodal LLMs for OCR, OCR Post-Correction, and Named Entity Recognition in Historical Documents

We explore how multimodal Large Language Models (mLLMs) can help researchers transcribe historical documents, extract relevant historical information, and construct datasets from historical sources. Specifically, we investigate the capabilities of mLLMs in performing (1) Optical Character Recognition (OCR), (2) OCR Post-Correction, and (3) Named Entity Recognition (NER) tasks on a set of city directories published in German between 1754 and 1870. First, we benchmark the off-the-shelf transcription accuracy of both mLLMs and conventional OCR models. We find that the best-performing mLLM model significantly outperforms conventional state-of-the-art OCR models and other frontier mLLMs. Second, we are the first to introduce multimodal post-correction of OCR output using mLLMs. We find that this novel approach leads to a drastic improvement in transcription accuracy and consistently produces highly accurate transcriptions (<1% CER), without any image pre-processing or model fine-tuning. Third, we demonstrate that mLLMs can efficiently recognize entities in transcriptions of historical documents and parse them into structured dataset formats. Our findings provide early evidence for the long-term potential of mLLMs to introduce a paradigm shift in the approaches to historical data collection and document transcription.

Physics-Preserving AI-Accelerated Simulations of Plasma Turbulence

Turbulence in fluids, gases, and plasmas remains an open problem of both practical and fundamental importance. Its irreducible complexity usually cannot be tackled computationally in a brute-force style. Here, we combine Large Eddy Simulation (LES) techniques with Machine Learning (ML) to retain only the largest dynamics explicitly, while small-scale dynamics are described by an ML-based sub-grid-scale model. Applying this novel approach to self-driven plasma turbulence allows us to remove large parts of the inertial range, reducing the computational effort by about three orders of magnitude, while retaining the statistical physical properties of the turbulent system.

Leveraging Stochastic Predictions of Bayesian Neural Networks for Fluid Simulations

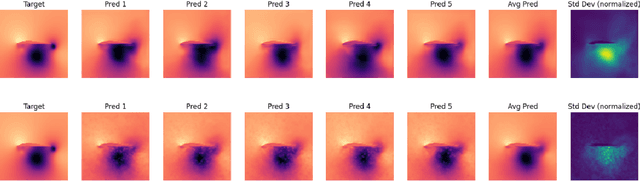
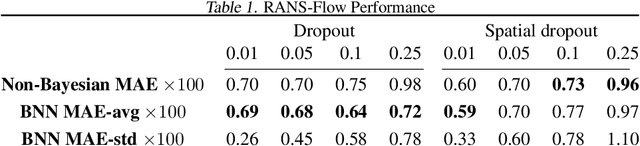
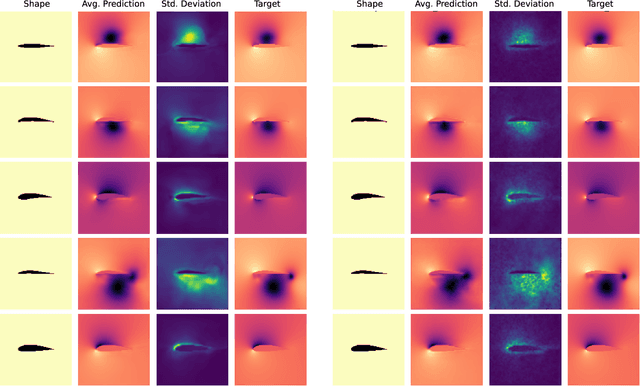
We investigate uncertainty estimation and multimodality via the non-deterministic predictions of Bayesian neural networks (BNNs) in fluid simulations. To this end, we deploy BNNs in three challenging experimental test-cases of increasing complexity: We show that BNNs, when used as surrogate models for steady-state fluid flow predictions, provide accurate physical predictions together with sensible estimates of uncertainty. Further, we experiment with perturbed temporal sequences from Navier-Stokes simulations and evaluate the capabilities of BNNs to capture multimodal evolutions. While our findings indicate that this is problematic for large perturbations, our results show that the networks learn to correctly predict high uncertainties in such situations. Finally, we study BNNs in the context of solver interactions with turbulent plasma flows. We find that BNN-based corrector networks can stabilize coarse-grained simulations and successfully create multimodal trajectories.