Frank Jenko
Machine Learning for Electron-Scale Turbulence Modeling in W7-X
Nov 06, 2025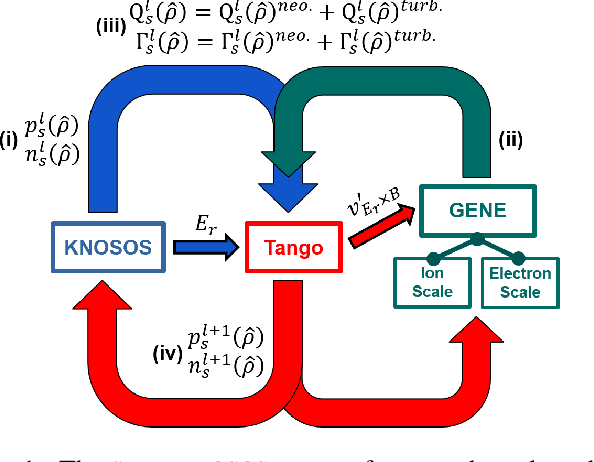
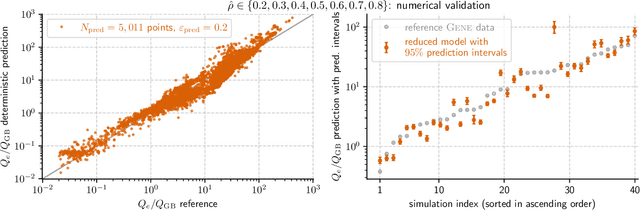
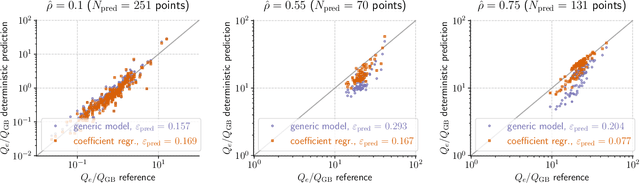
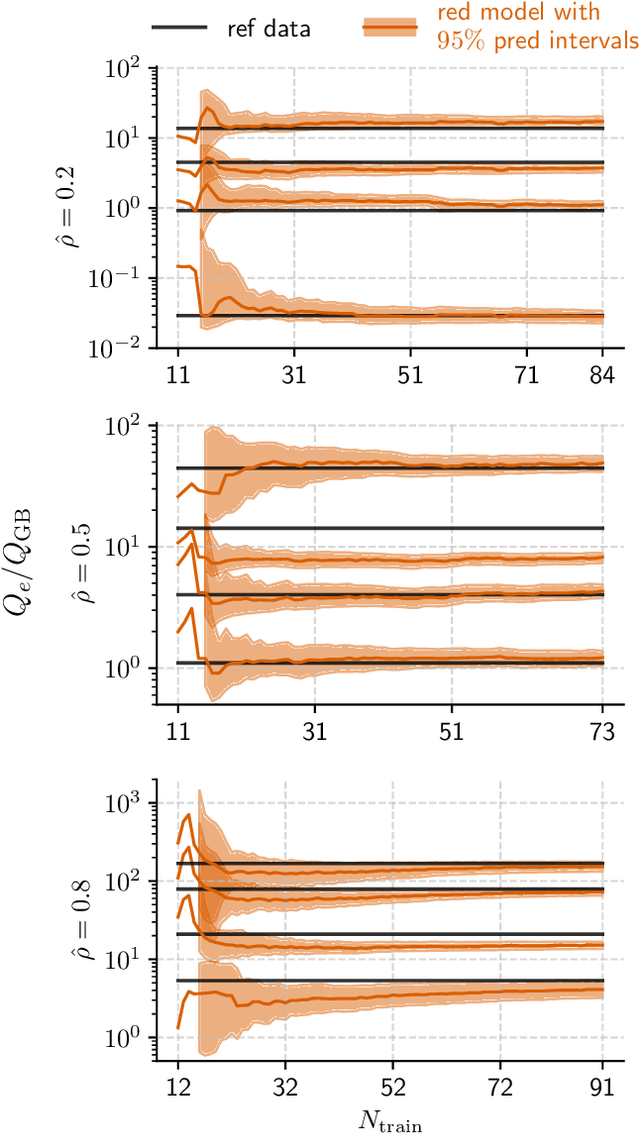
Abstract:Constructing reduced models for turbulent transport is essential for accelerating profile predictions and enabling many-query tasks such as uncertainty quantification, parameter scans, and design optimization. This paper presents machine-learning-driven reduced models for Electron Temperature Gradient (ETG) turbulence in the Wendelstein 7-X (W7-X) stellarator. Each model predicts the ETG heat flux as a function of three plasma parameters: the normalized electron temperature radial gradient ($\omega_{T_e}$), the ratio of normalized electron temperature and density radial gradients ($\eta_e$), and the electron-to-ion temperature ratio ($\tau$). We first construct models across seven radial locations using regression and an active machine-learning-based procedure. This process initializes models using low-cardinality sparse-grid training data and then iteratively refines their training sets by selecting the most informative points from a pre-existing simulation database. We evaluate the prediction capabilities of our models using out-of-sample datasets with over $393$ points per location, and $95\%$ prediction intervals are estimated via bootstrapping to assess prediction uncertainty. We then investigate the construction of generalized reduced models, including a generic, position-independent model, and assess their heat flux prediction capabilities at three additional locations. Our models demonstrate robust performance and predictive accuracy comparable to the original reference simulations, even when applied beyond the training domain.
Learning physics-based reduced models from data for the Hasegawa-Wakatani equations
Jan 11, 2024



Abstract:This paper focuses on the construction of non-intrusive Scientific Machine Learning (SciML) Reduced-Order Models (ROMs) for nonlinear, chaotic plasma turbulence simulations. In particular, we propose using Operator Inference (OpInf) to build low-cost physics-based ROMs from data for such simulations. As a representative example, we focus on the Hasegawa-Wakatani (HW) equations used for modeling two-dimensional electrostatic drift-wave plasma turbulence. For a comprehensive perspective of the potential of OpInf to construct accurate ROMs for this model, we consider a setup for the HW equations that leads to the formation of complex, nonlinear, and self-driven dynamics, and perform two sets of experiments. We first use the data obtained via a direct numerical simulation of the HW equations starting from a specific initial condition and train OpInf ROMs for predictions beyond the training time horizon. In the second, more challenging set of experiments, we train ROMs using the same dataset as before but this time perform predictions for six other initial conditions. Our results show that the OpInf ROMs capture the important features of the turbulent dynamics and generalize to new and unseen initial conditions while reducing the evaluation time of the high-fidelity model by up to five orders of magnitude in single-core performance. In the broader context of fusion research, this shows that non-intrusive SciML ROMs have the potential to drastically accelerate numerical studies, which can ultimately enable tasks such as the design and real-time control of optimized fusion devices.
Physics-Preserving AI-Accelerated Simulations of Plasma Turbulence
Sep 28, 2023Abstract:Turbulence in fluids, gases, and plasmas remains an open problem of both practical and fundamental importance. Its irreducible complexity usually cannot be tackled computationally in a brute-force style. Here, we combine Large Eddy Simulation (LES) techniques with Machine Learning (ML) to retain only the largest dynamics explicitly, while small-scale dynamics are described by an ML-based sub-grid-scale model. Applying this novel approach to self-driven plasma turbulence allows us to remove large parts of the inertial range, reducing the computational effort by about three orders of magnitude, while retaining the statistical physical properties of the turbulent system.
Context-aware learning of hierarchies of low-fidelity models for multi-fidelity uncertainty quantification
Nov 20, 2022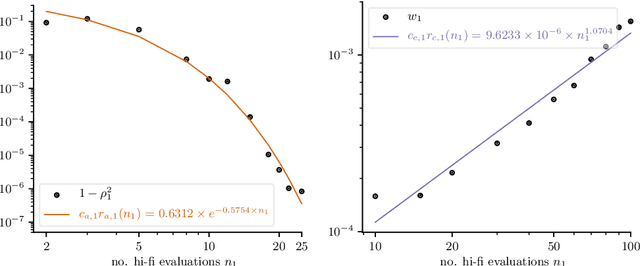

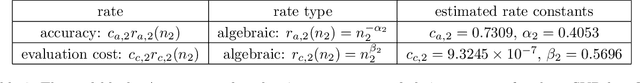
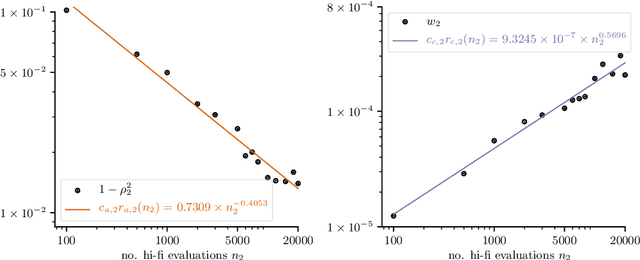
Abstract:Multi-fidelity Monte Carlo methods leverage low-fidelity and surrogate models for variance reduction to make tractable uncertainty quantification even when numerically simulating the physical systems of interest with high-fidelity models is computationally expensive. This work proposes a context-aware multi-fidelity Monte Carlo method that optimally balances the costs of training low-fidelity models with the costs of Monte Carlo sampling. It generalizes the previously developed context-aware bi-fidelity Monte Carlo method to hierarchies of multiple models and to more general types of low-fidelity models. When training low-fidelity models, the proposed approach takes into account the context in which the learned low-fidelity models will be used, namely for variance reduction in Monte Carlo estimation, which allows it to find optimal trade-offs between training and sampling to minimize upper bounds of the mean-squared errors of the estimators for given computational budgets. This is in stark contrast to traditional surrogate modeling and model reduction techniques that construct low-fidelity models with the primary goal of approximating well the high-fidelity model outputs and typically ignore the context in which the learned models will be used in upstream tasks. The proposed context-aware multi-fidelity Monte Carlo method applies to hierarchies of a wide range of types of low-fidelity models such as sparse-grid and deep-network models. Numerical experiments with the gyrokinetic simulation code \textsc{Gene} show speedups of up to two orders of magnitude compared to standard estimators when quantifying uncertainties in small-scale fluctuations in confined plasma in fusion reactors. This corresponds to a runtime reduction from 72 days to about four hours on one node of the Lonestar6 supercomputer at the Texas Advanced Computing Center.
Leveraging Stochastic Predictions of Bayesian Neural Networks for Fluid Simulations
May 02, 2022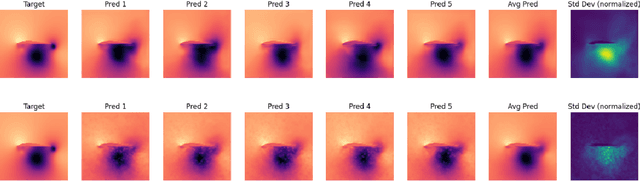
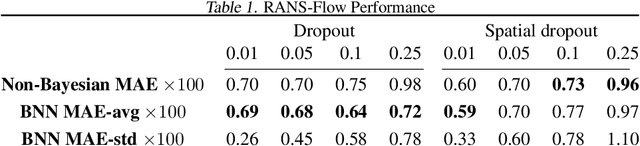
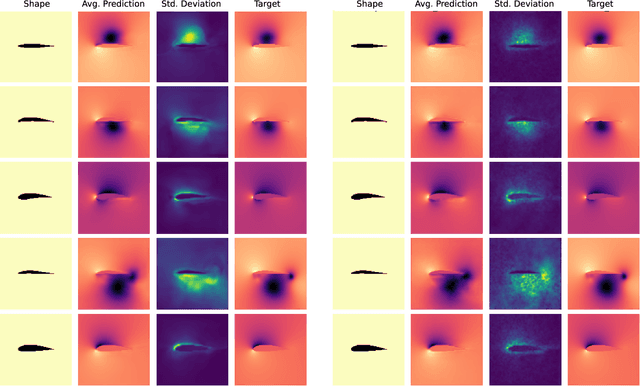

Abstract:We investigate uncertainty estimation and multimodality via the non-deterministic predictions of Bayesian neural networks (BNNs) in fluid simulations. To this end, we deploy BNNs in three challenging experimental test-cases of increasing complexity: We show that BNNs, when used as surrogate models for steady-state fluid flow predictions, provide accurate physical predictions together with sensible estimates of uncertainty. Further, we experiment with perturbed temporal sequences from Navier-Stokes simulations and evaluate the capabilities of BNNs to capture multimodal evolutions. While our findings indicate that this is problematic for large perturbations, our results show that the networks learn to correctly predict high uncertainties in such situations. Finally, we study BNNs in the context of solver interactions with turbulent plasma flows. We find that BNN-based corrector networks can stabilize coarse-grained simulations and successfully create multimodal trajectories.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge