Parametric model reduction of mean-field and stochastic systems via higher-order action matching

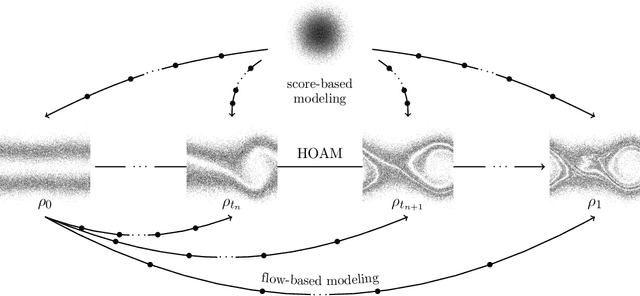
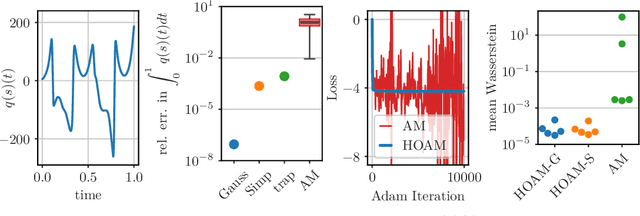
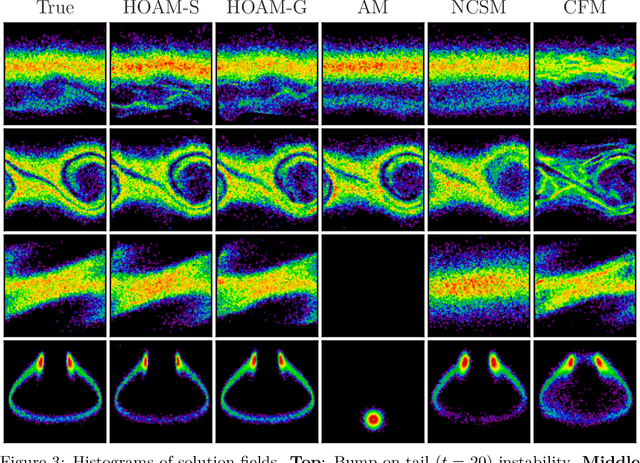
The aim of this work is to learn models of population dynamics of physical systems that feature stochastic and mean-field effects and that depend on physics parameters. The learned models can act as surrogates of classical numerical models to efficiently predict the system behavior over the physics parameters. Building on the Benamou-Brenier formula from optimal transport and action matching, we use a variational problem to infer parameter- and time-dependent gradient fields that represent approximations of the population dynamics. The inferred gradient fields can then be used to rapidly generate sample trajectories that mimic the dynamics of the physical system on a population level over varying physics parameters. We show that combining Monte Carlo sampling with higher-order quadrature rules is critical for accurately estimating the training objective from sample data and for stabilizing the training process. We demonstrate on Vlasov-Poisson instabilities as well as on high-dimensional particle and chaotic systems that our approach accurately predicts population dynamics over a wide range of parameters and outperforms state-of-the-art diffusion-based and flow-based modeling that simply condition on time and physics parameters.

System stabilization with policy optimization on unstable latent manifolds

Stability is a basic requirement when studying the behavior of dynamical systems. However, stabilizing dynamical systems via reinforcement learning is challenging because only little data can be collected over short time horizons before instabilities are triggered and data become meaningless. This work introduces a reinforcement learning approach that is formulated over latent manifolds of unstable dynamics so that stabilizing policies can be trained from few data samples. The unstable manifolds are minimal in the sense that they contain the lowest dimensional dynamics that are necessary for learning policies that guarantee stabilization. This is in stark contrast to generic latent manifolds that aim to approximate all -- stable and unstable -- system dynamics and thus are higher dimensional and often require higher amounts of data. Experiments demonstrate that the proposed approach stabilizes even complex physical systems from few data samples for which other methods that operate either directly in the system state space or on generic latent manifolds fail.

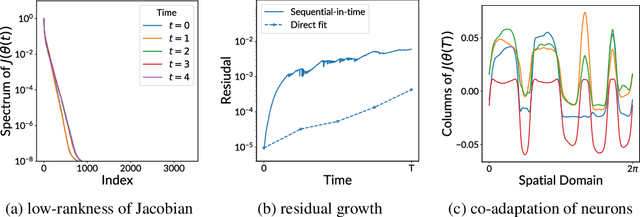
Sequential-in-time training of nonlinear parametrizations for solving time-dependent partial differential equations

Sequential-in-time methods solve a sequence of training problems to fit nonlinear parametrizations such as neural networks to approximate solution trajectories of partial differential equations over time. This work shows that sequential-in-time training methods can be understood broadly as either optimize-then-discretize (OtD) or discretize-then-optimize (DtO) schemes, which are well known concepts in numerical analysis. The unifying perspective leads to novel stability and a posteriori error analysis results that provide insights into theoretical and numerical aspects that are inherent to either OtD or DtO schemes such as the tangent space collapse phenomenon, which is a form of over-fitting. Additionally, the unified perspective facilitates establishing connections between variants of sequential-in-time training methods, which is demonstrated by identifying natural gradient descent methods on energy functionals as OtD schemes applied to the corresponding gradient flows.

CoLoRA: Continuous low-rank adaptation for reduced implicit neural modeling of parameterized partial differential equations

This work introduces reduced models based on Continuous Low Rank Adaptation (CoLoRA) that pre-train neural networks for a given partial differential equation and then continuously adapt low-rank weights in time to rapidly predict the evolution of solution fields at new physics parameters and new initial conditions. The adaptation can be either purely data-driven or via an equation-driven variational approach that provides Galerkin-optimal approximations. Because CoLoRA approximates solution fields locally in time, the rank of the weights can be kept small, which means that only few training trajectories are required offline so that CoLoRA is well suited for data-scarce regimes. Predictions with CoLoRA are orders of magnitude faster than with classical methods and their accuracy and parameter efficiency is higher compared to other neural network approaches.

Nonlinear embeddings for conserving Hamiltonians and other quantities with Neural Galerkin schemes

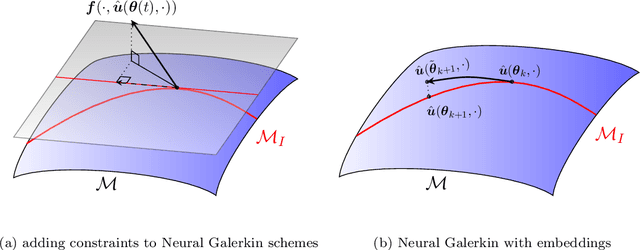
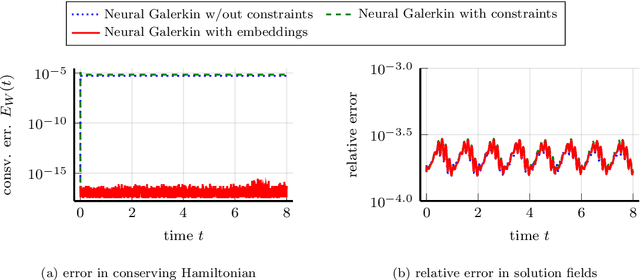
This work focuses on the conservation of quantities such as Hamiltonians, mass, and momentum when solution fields of partial differential equations are approximated with nonlinear parametrizations such as deep networks. The proposed approach builds on Neural Galerkin schemes that are based on the Dirac--Frenkel variational principle to train nonlinear parametrizations sequentially in time. We first show that only adding constraints that aim to conserve quantities in continuous time can be insufficient because the nonlinear dependence on the parameters implies that even quantities that are linear in the solution fields become nonlinear in the parameters and thus are challenging to discretize in time. Instead, we propose Neural Galerkin schemes that compute at each time step an explicit embedding onto the manifold of nonlinearly parametrized solution fields to guarantee conservation of quantities. The embeddings can be combined with standard explicit and implicit time integration schemes. Numerical experiments demonstrate that the proposed approach conserves quantities up to machine precision.

Randomized Sparse Neural Galerkin Schemes for Solving Evolution Equations with Deep Networks

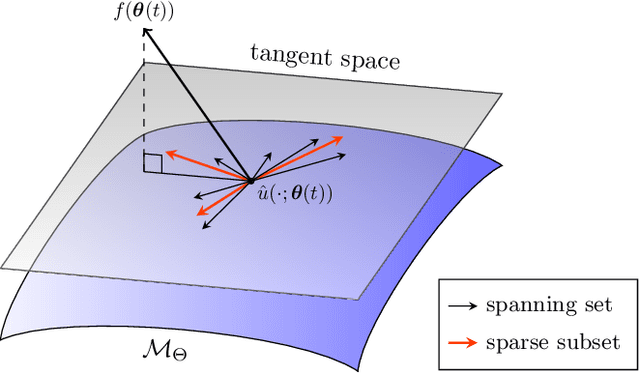
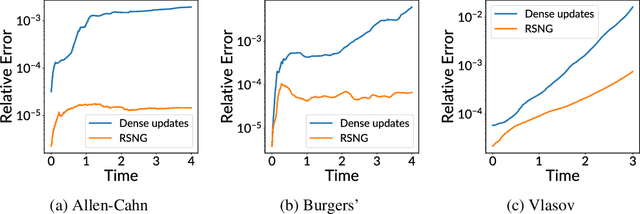
Training neural networks sequentially in time to approximate solution fields of time-dependent partial differential equations can be beneficial for preserving causality and other physics properties; however, the sequential-in-time training is numerically challenging because training errors quickly accumulate and amplify over time. This work introduces Neural Galerkin schemes that update randomized sparse subsets of network parameters at each time step. The randomization avoids overfitting locally in time and so helps prevent the error from accumulating quickly over the sequential-in-time training, which is motivated by dropout that addresses a similar issue of overfitting due to neuron co-adaptation. The sparsity of the update reduces the computational costs of training without losing expressiveness because many of the network parameters are redundant locally at each time step. In numerical experiments with a wide range of evolution equations, the proposed scheme with randomized sparse updates is up to two orders of magnitude more accurate at a fixed computational budget and up to two orders of magnitude faster at a fixed accuracy than schemes with dense updates.

Multifidelity Covariance Estimation via Regression on the Manifold of Symmetric Positive Definite Matrices

We introduce a multifidelity estimator of covariance matrices formulated as the solution to a regression problem on the manifold of symmetric positive definite matrices. The estimator is positive definite by construction, and the Mahalanobis distance minimized to obtain it possesses properties which enable practical computation. We show that our manifold regression multifidelity (MRMF) covariance estimator is a maximum likelihood estimator under a certain error model on manifold tangent space. More broadly, we show that our Riemannian regression framework encompasses existing multifidelity covariance estimators constructed from control variates. We demonstrate via numerical examples that our estimator can provide significant decreases, up to one order of magnitude, in squared estimation error relative to both single-fidelity and other multifidelity covariance estimators. Furthermore, preservation of positive definiteness ensures that our estimator is compatible with downstream tasks, such as data assimilation and metric learning, in which this property is essential.

Coupling parameter and particle dynamics for adaptive sampling in Neural Galerkin schemes

Training nonlinear parametrizations such as deep neural networks to numerically approximate solutions of partial differential equations is often based on minimizing a loss that includes the residual, which is analytically available in limited settings only. At the same time, empirically estimating the training loss is challenging because residuals and related quantities can have high variance, especially for transport-dominated and high-dimensional problems that exhibit local features such as waves and coherent structures. Thus, estimators based on data samples from un-informed, uniform distributions are inefficient. This work introduces Neural Galerkin schemes that estimate the training loss with data from adaptive distributions, which are empirically represented via ensembles of particles. The ensembles are actively adapted by evolving the particles with dynamics coupled to the nonlinear parametrizations of the solution fields so that the ensembles remain informative for estimating the training loss. Numerical experiments indicate that few dynamic particles are sufficient for obtaining accurate empirical estimates of the training loss, even for problems with local features and with high-dimensional spatial domains.

Rank-Minimizing and Structured Model Inference

While extracting information from data with machine learning plays an increasingly important role, physical laws and other first principles continue to provide critical insights about systems and processes of interest in science and engineering. This work introduces a method that infers models from data with physical insights encoded in the form of structure and that minimizes the model order so that the training data are fitted well while redundant degrees of freedom without conditions and sufficient data to fix them are automatically eliminated. The models are formulated via solution matrices of specific instances of generalized Sylvester equations that enforce interpolation of the training data and relate the model order to the rank of the solution matrices. The proposed method numerically solves the Sylvester equations for minimal-rank solutions and so obtains models of low order. Numerical experiments demonstrate that the combination of structure preservation and rank minimization leads to accurate models with orders of magnitude fewer degrees of freedom than models of comparable prediction quality that are learned with structure preservation alone.

Multi-fidelity covariance estimation in the log-Euclidean geometry

We introduce a multi-fidelity estimator of covariance matrices that employs the log-Euclidean geometry of the symmetric positive-definite manifold. The estimator fuses samples from a hierarchy of data sources of differing fidelities and costs for variance reduction while guaranteeing definiteness, in contrast with previous approaches. The new estimator makes covariance estimation tractable in applications where simulation or data collection is expensive; to that end, we develop an optimal sample allocation scheme that minimizes the mean-squared error of the estimator given a fixed budget. Guaranteed definiteness is crucial to metric learning, data assimilation, and other downstream tasks. Evaluations of our approach using data from physical applications (heat conduction, fluid dynamics) demonstrate more accurate metric learning and speedups of more than one order of magnitude compared to benchmarks.