Multifidelity Covariance Estimation via Regression on the Manifold of Symmetric Positive Definite Matrices

We introduce a multifidelity estimator of covariance matrices formulated as the solution to a regression problem on the manifold of symmetric positive definite matrices. The estimator is positive definite by construction, and the Mahalanobis distance minimized to obtain it possesses properties which enable practical computation. We show that our manifold regression multifidelity (MRMF) covariance estimator is a maximum likelihood estimator under a certain error model on manifold tangent space. More broadly, we show that our Riemannian regression framework encompasses existing multifidelity covariance estimators constructed from control variates. We demonstrate via numerical examples that our estimator can provide significant decreases, up to one order of magnitude, in squared estimation error relative to both single-fidelity and other multifidelity covariance estimators. Furthermore, preservation of positive definiteness ensures that our estimator is compatible with downstream tasks, such as data assimilation and metric learning, in which this property is essential.

Multi-fidelity covariance estimation in the log-Euclidean geometry

We introduce a multi-fidelity estimator of covariance matrices that employs the log-Euclidean geometry of the symmetric positive-definite manifold. The estimator fuses samples from a hierarchy of data sources of differing fidelities and costs for variance reduction while guaranteeing definiteness, in contrast with previous approaches. The new estimator makes covariance estimation tractable in applications where simulation or data collection is expensive; to that end, we develop an optimal sample allocation scheme that minimizes the mean-squared error of the estimator given a fixed budget. Guaranteed definiteness is crucial to metric learning, data assimilation, and other downstream tasks. Evaluations of our approach using data from physical applications (heat conduction, fluid dynamics) demonstrate more accurate metric learning and speedups of more than one order of magnitude compared to benchmarks.

Further analysis of multilevel Stein variational gradient descent with an application to the Bayesian inference of glacier ice models

Multilevel Stein variational gradient descent is a method for particle-based variational inference that leverages hierarchies of approximations of target distributions with varying costs and fidelity to computationally speed up inference. This work provides a cost complexity analysis of multilevel Stein variational gradient descent that applies under milder conditions than previous results, especially in discrete-in-time regimes and beyond the limited settings where Stein variational gradient descent achieves exponentially fast convergence. The analysis shows that the convergence rate of Stein variational gradient descent enters only as a constant factor for the cost complexity of the multilevel version, which means that the costs of the multilevel version scale independently of the convergence rate of Stein variational gradient descent on a single level. Numerical experiments with Bayesian inverse problems of inferring discretized basal sliding coefficient fields of the Arolla glacier ice demonstrate that multilevel Stein variational gradient descent achieves orders of magnitude speedups compared to its single-level version.

Multilevel Stein variational gradient descent with applications to Bayesian inverse problems

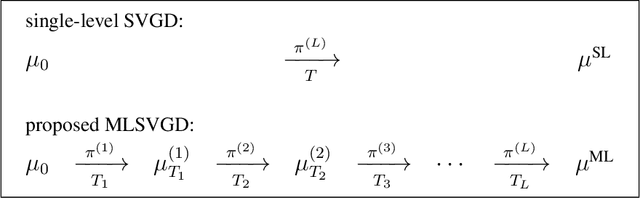
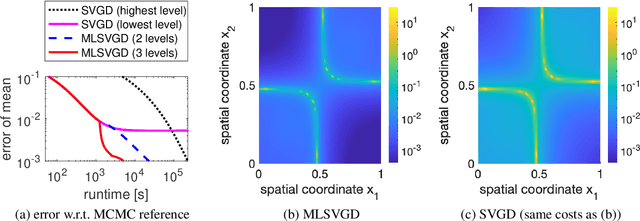
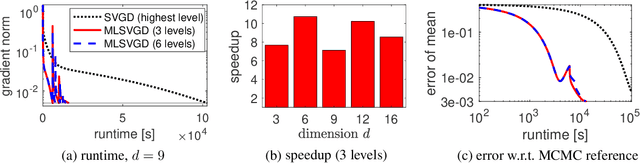
This work presents a multilevel variant of Stein variational gradient descent to more efficiently sample from target distributions. The key ingredient is a sequence of distributions with growing fidelity and costs that converges to the target distribution of interest. For example, such a sequence of distributions is given by a hierarchy of ever finer discretization levels of the forward model in Bayesian inverse problems. The proposed multilevel Stein variational gradient descent moves most of the iterations to lower, cheaper levels with the aim of requiring only a few iterations on the higher, more expensive levels when compared to the traditional, single-level Stein variational gradient descent variant that uses the highest-level distribution only. Under certain assumptions, in the mean-field limit, the error of the proposed multilevel Stein method decays by a log factor faster than the error of the single-level counterpart with respect to computational costs. Numerical experiments with Bayesian inverse problems show speedups of more than one order of magnitude of the proposed multilevel Stein method compared to the single-level variant that uses the highest level only.

Context-aware surrogate modeling for balancing approximation and sampling costs in multi-fidelity importance sampling and Bayesian inverse problems

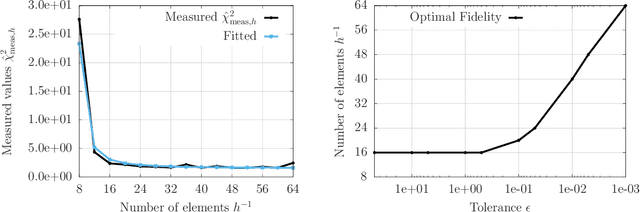
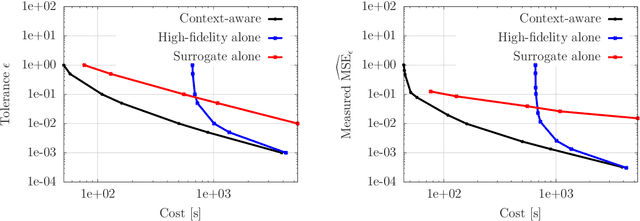
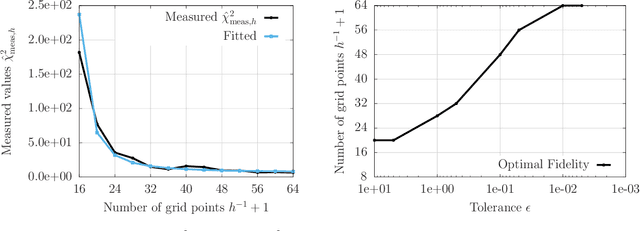
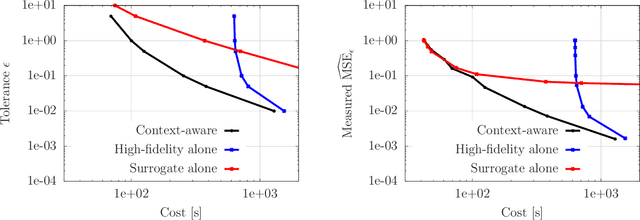
Multi-fidelity methods leverage low-cost surrogate models to speed up computations and make occasional recourse to expensive high-fidelity models to establish accuracy guarantees. Because surrogate and high-fidelity models are used together, poor predictions by the surrogate models can be compensated with frequent recourse to high-fidelity models. Thus, there is a trade-off between investing computational resources to improve surrogate models and the frequency of making recourse to expensive high-fidelity models; however, this trade-off is ignored by traditional modeling methods that construct surrogate models that are meant to replace high-fidelity models rather than being used together with high-fidelity models. This work considers multi-fidelity importance sampling and theoretically and computationally derives the optimal trade-off between improving the fidelity of surrogate models for constructing more accurate biasing densities and the number of samples that is required from the high-fidelity model to compensate poor biasing densities. Numerical examples demonstrate that such optimal---context-aware---surrogate models for multi-fidelity importance sampling have lower fidelity than what typically is set as tolerance in traditional model reduction, leading to runtime speedups of up to one order of magnitude in the presented examples.