Context-aware surrogate modeling for balancing approximation and sampling costs in multi-fidelity importance sampling and Bayesian inverse problems

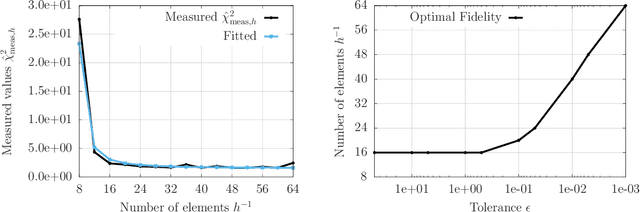
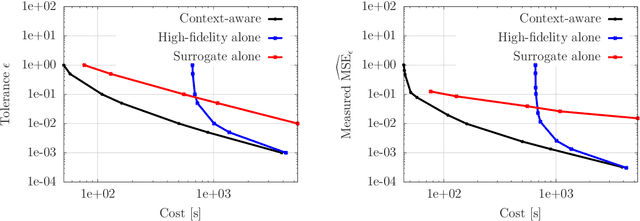
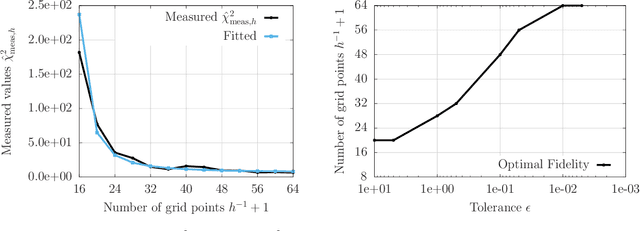
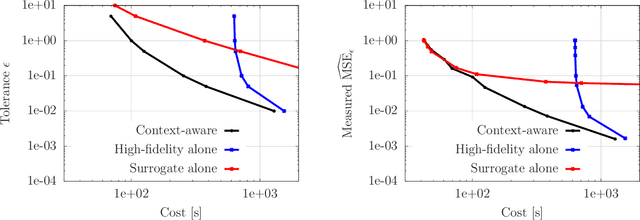
Multi-fidelity methods leverage low-cost surrogate models to speed up computations and make occasional recourse to expensive high-fidelity models to establish accuracy guarantees. Because surrogate and high-fidelity models are used together, poor predictions by the surrogate models can be compensated with frequent recourse to high-fidelity models. Thus, there is a trade-off between investing computational resources to improve surrogate models and the frequency of making recourse to expensive high-fidelity models; however, this trade-off is ignored by traditional modeling methods that construct surrogate models that are meant to replace high-fidelity models rather than being used together with high-fidelity models. This work considers multi-fidelity importance sampling and theoretically and computationally derives the optimal trade-off between improving the fidelity of surrogate models for constructing more accurate biasing densities and the number of samples that is required from the high-fidelity model to compensate poor biasing densities. Numerical examples demonstrate that such optimal---context-aware---surrogate models for multi-fidelity importance sampling have lower fidelity than what typically is set as tolerance in traditional model reduction, leading to runtime speedups of up to one order of magnitude in the presented examples.