Generative Modeling through Spectral Analysis of Koopman Operator

We propose Koopman Spectral Wasserstein Gradient Descent (KSWGD), a generative modeling framework that combines operator-theoretic spectral analysis with optimal transport. The novel insight is that the spectral structure required for accelerated Wasserstein gradient descent can be directly estimated from trajectory data via Koopman operator approximation which can eliminate the need for explicit knowledge of the target potential or neural network training. We provide rigorous convergence analysis and establish connection to Feynman-Kac theory that clarifies the method's probabilistic foundation. Experiments across diverse settings, including compact manifold sampling, metastable multi-well systems, image generation, and high dimensional stochastic partial differential equation, demonstrate that KSWGD consistently achieves faster convergence than other existing methods while maintaining high sample quality.

Learning Paths for Dynamic Measure Transport: A Control Perspective

We bring a control perspective to the problem of identifying paths of measures for sampling via dynamic measure transport (DMT). We highlight the fact that commonly used paths may be poor choices for DMT and connect existing methods for learning alternate paths to mean-field games. Based on these connections we pose a flexible family of optimization problems for identifying tilted paths of measures for DMT and advocate for the use of objective terms which encourage smoothness of the corresponding velocities. We present a numerical algorithm for solving these problems based on recent Gaussian process methods for solution of partial differential equations and demonstrate the ability of our method to recover more efficient and smooth transport models compared to those which use an untilted reference path.

Canonical Bayesian Linear System Identification

Standard Bayesian approaches for linear time-invariant (LTI) system identification are hindered by parameter non-identifiability; the resulting complex, multi-modal posteriors make inference inefficient and impractical. We solve this problem by embedding canonical forms of LTI systems within the Bayesian framework. We rigorously establish that inference in these minimal parameterizations fully captures all invariant system dynamics (e.g., transfer functions, eigenvalues, predictive distributions of system outputs) while resolving identifiability. This approach unlocks the use of meaningful, structure-aware priors (e.g., enforcing stability via eigenvalues) and ensures conditions for a Bernstein--von Mises theorem -- a link between Bayesian and frequentist large-sample asymptotics that is broken in standard forms. Extensive simulations with modern MCMC methods highlight advantages over standard parameterizations: canonical forms achieve higher computational efficiency, generate interpretable and well-behaved posteriors, and provide robust uncertainty estimates, particularly from limited data.

Localized Diffusion Models for High Dimensional Distributions Generation

Diffusion models are the state-of-the-art tools for various generative tasks. However, estimating high-dimensional score functions makes them potentially suffer from the curse of dimensionality (CoD). This underscores the importance of better understanding and exploiting low-dimensional structure in the target distribution. In this work, we consider locality structure, which describes sparse dependencies between model components. Under locality structure, the score function is effectively low-dimensional, so that it can be estimated by a localized neural network with significantly reduced sample complexity. This motivates the localized diffusion model, where a localized score matching loss is used to train the score function within a localized hypothesis space. We prove that such localization enables diffusion models to circumvent CoD, at the price of additional localization error. Under realistic sample size scaling, we show both theoretically and numerically that a moderate localization radius can balance the statistical and localization error, leading to a better overall performance. The localized structure also facilitates parallel training of diffusion models, making it potentially more efficient for large-scale applications.

Optimal Scheduling of Dynamic Transport

Flow-based methods for sampling and generative modeling use continuous-time dynamical systems to represent a {transport map} that pushes forward a source measure to a target measure. The introduction of a time axis provides considerable design freedom, and a central question is how to exploit this freedom. Though many popular methods seek straight line (i.e., zero acceleration) trajectories, we show here that a specific class of ``curved'' trajectories can significantly improve approximation and learning. In particular, we consider the unit-time interpolation of any given transport map $T$ and seek the schedule $\tau: [0,1] \to [0,1]$ that minimizes the spatial Lipschitz constant of the corresponding velocity field over all times $t \in [0,1]$. This quantity is crucial as it allows for control of the approximation error when the velocity field is learned from data. We show that, for a broad class of source/target measures and transport maps $T$, the \emph{optimal schedule} can be computed in closed form, and that the resulting optimal Lipschitz constant is \emph{exponentially smaller} than that induced by an identity schedule (corresponding to, for instance, the Wasserstein geodesic). Our proof technique relies on the calculus of variations and $\Gamma$-convergence, allowing us to approximate the aforementioned degenerate objective by a family of smooth, tractable problems.

A friendly introduction to triangular transport

Decision making under uncertainty is a cross-cutting challenge in science and engineering. Most approaches to this challenge employ probabilistic representations of uncertainty. In complicated systems accessible only via data or black-box models, however, these representations are rarely known. We discuss how to characterize and manipulate such representations using triangular transport maps, which approximate any complex probability distribution as a transformation of a simple, well-understood distribution. The particular structure of triangular transport guarantees many desirable mathematical and computational properties that translate well into solving practical problems. Triangular maps are actively used for density estimation, (conditional) generative modelling, Bayesian inference, data assimilation, optimal experimental design, and related tasks. While there is ample literature on the development and theory of triangular transport methods, this manuscript provides a detailed introduction for scientists interested in employing measure transport without assuming a formal mathematical background. We build intuition for the key foundations of triangular transport, discuss many aspects of its practical implementation, and outline the frontiers of this field.

Learning local neighborhoods of non-Gaussian graphical models: A measure transport approach

Identifying the Markov properties or conditional independencies of a collection of random variables is a fundamental task in statistics for modeling and inference. Existing approaches often learn the structure of a probabilistic graphical model, which encodes these dependencies, by assuming that the variables follow a distribution with a simple parametric form. Moreover, the computational cost of many algorithms scales poorly for high-dimensional distributions, as they need to estimate all the edges in the graph simultaneously. In this work, we propose a scalable algorithm to infer the conditional independence relationships of each variable by exploiting the local Markov property. The proposed method, named Localized Sparsity Identification for Non-Gaussian Distributions (L-SING), estimates the graph by using flexible classes of transport maps to represent the conditional distribution for each variable. We show that L-SING includes existing approaches, such as neighborhood selection with Lasso, as a special case. We demonstrate the effectiveness of our algorithm in both Gaussian and non-Gaussian settings by comparing it to existing methods. Lastly, we show the scalability of the proposed approach by applying it to high-dimensional non-Gaussian examples, including a biological dataset with more than 150 variables.

Conformal Prediction under Lévy-Prokhorov Distribution Shifts: Robustness to Local and Global Perturbations

Conformal prediction provides a powerful framework for constructing prediction intervals with finite-sample guarantees, yet its robustness under distribution shifts remains a significant challenge. This paper addresses this limitation by modeling distribution shifts using L\'evy-Prokhorov (LP) ambiguity sets, which capture both local and global perturbations. We provide a self-contained overview of LP ambiguity sets and their connections to popular metrics such as Wasserstein and Total Variation. We show that the link between conformal prediction and LP ambiguity sets is a natural one: by propagating the LP ambiguity set through the scoring function, we reduce complex high-dimensional distribution shifts to manageable one-dimensional distribution shifts, enabling exact quantification of worst-case quantiles and coverage. Building on this analysis, we construct robust conformal prediction intervals that remain valid under distribution shifts, explicitly linking LP parameters to interval width and confidence levels. Experimental results on real-world datasets demonstrate the effectiveness of the proposed approach.

Can Bayesian Neural Networks Make Confident Predictions?

Bayesian inference promises a framework for principled uncertainty quantification of neural network predictions. Barriers to adoption include the difficulty of fully characterizing posterior distributions on network parameters and the interpretability of posterior predictive distributions. We demonstrate that under a discretized prior for the inner layer weights, we can exactly characterize the posterior predictive distribution as a Gaussian mixture. This setting allows us to define equivalence classes of network parameter values which produce the same likelihood (training error) and to relate the elements of these classes to the network's scaling regime -- defined via ratios of the training sample size, the size of each layer, and the number of final layer parameters. Of particular interest are distinct parameter realizations that map to low training error and yet correspond to distinct modes in the posterior predictive distribution. We identify settings that exhibit such predictive multimodality, and thus provide insight into the accuracy of unimodal posterior approximations. We also characterize the capacity of a model to "learn from data" by evaluating contraction of the posterior predictive in different scaling regimes.

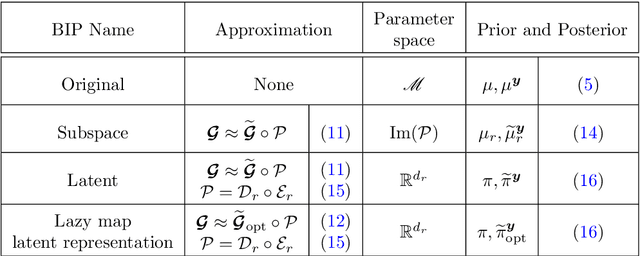
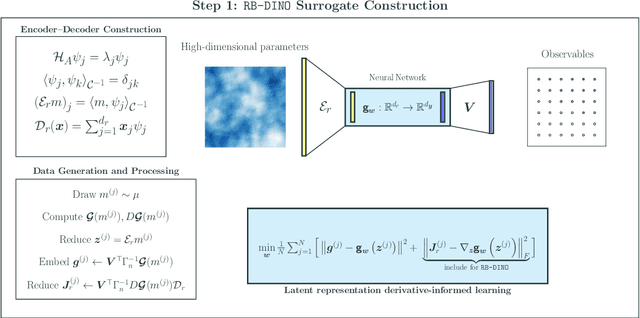
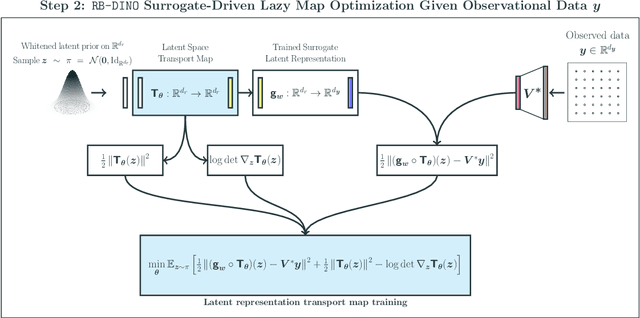
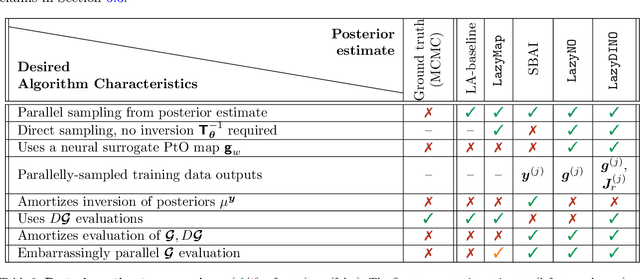
LazyDINO: Fast, scalable, and efficiently amortized Bayesian inversion via structure-exploiting and surrogate-driven measure transport

We present LazyDINO, a transport map variational inference method for fast, scalable, and efficiently amortized solutions of high-dimensional nonlinear Bayesian inverse problems with expensive parameter-to-observable (PtO) maps. Our method consists of an offline phase in which we construct a derivative-informed neural surrogate of the PtO map using joint samples of the PtO map and its Jacobian. During the online phase, when given observational data, we seek rapid posterior approximation using surrogate-driven training of a lazy map [Brennan et al., NeurIPS, (2020)], i.e., a structure-exploiting transport map with low-dimensional nonlinearity. The trained lazy map then produces approximate posterior samples or density evaluations. Our surrogate construction is optimized for amortized Bayesian inversion using lazy map variational inference. We show that (i) the derivative-based reduced basis architecture [O'Leary-Roseberry et al., Comput. Methods Appl. Mech. Eng., 388 (2022)] minimizes the upper bound on the expected error in surrogate posterior approximation, and (ii) the derivative-informed training formulation [O'Leary-Roseberry et al., J. Comput. Phys., 496 (2024)] minimizes the expected error due to surrogate-driven transport map optimization. Our numerical results demonstrate that LazyDINO is highly efficient in cost amortization for Bayesian inversion. We observe one to two orders of magnitude reduction of offline cost for accurate posterior approximation, compared to simulation-based amortized inference via conditional transport and conventional surrogate-driven transport. In particular, LazyDINO outperforms Laplace approximation consistently using fewer than 1000 offline samples, while other amortized inference methods struggle and sometimes fail at 16,000 offline samples.