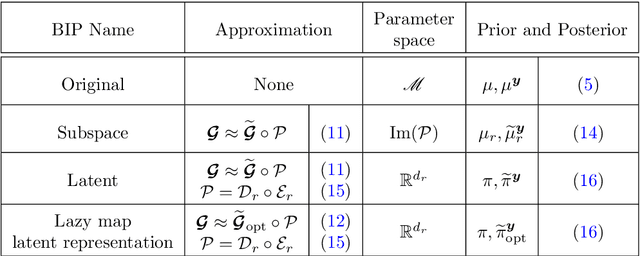
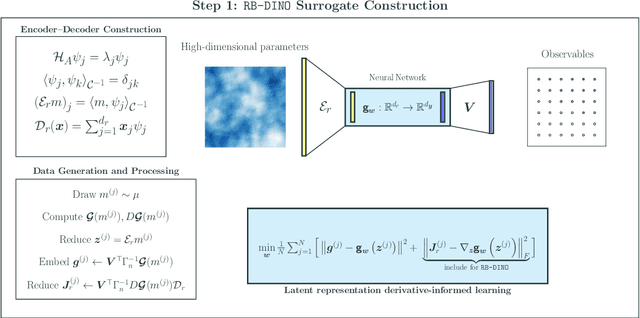
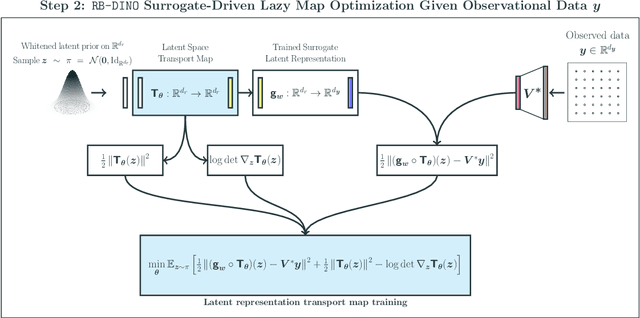
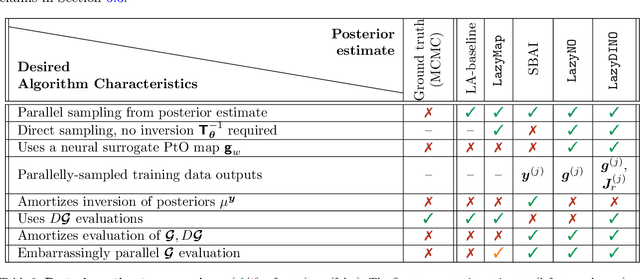
LazyDINO: Fast, scalable, and efficiently amortized Bayesian inversion via structure-exploiting and surrogate-driven measure transport

We present LazyDINO, a transport map variational inference method for fast, scalable, and efficiently amortized solutions of high-dimensional nonlinear Bayesian inverse problems with expensive parameter-to-observable (PtO) maps. Our method consists of an offline phase in which we construct a derivative-informed neural surrogate of the PtO map using joint samples of the PtO map and its Jacobian. During the online phase, when given observational data, we seek rapid posterior approximation using surrogate-driven training of a lazy map [Brennan et al., NeurIPS, (2020)], i.e., a structure-exploiting transport map with low-dimensional nonlinearity. The trained lazy map then produces approximate posterior samples or density evaluations. Our surrogate construction is optimized for amortized Bayesian inversion using lazy map variational inference. We show that (i) the derivative-based reduced basis architecture [O'Leary-Roseberry et al., Comput. Methods Appl. Mech. Eng., 388 (2022)] minimizes the upper bound on the expected error in surrogate posterior approximation, and (ii) the derivative-informed training formulation [O'Leary-Roseberry et al., J. Comput. Phys., 496 (2024)] minimizes the expected error due to surrogate-driven transport map optimization. Our numerical results demonstrate that LazyDINO is highly efficient in cost amortization for Bayesian inversion. We observe one to two orders of magnitude reduction of offline cost for accurate posterior approximation, compared to simulation-based amortized inference via conditional transport and conventional surrogate-driven transport. In particular, LazyDINO outperforms Laplace approximation consistently using fewer than 1000 offline samples, while other amortized inference methods struggle and sometimes fail at 16,000 offline samples.

Conditional simulation via entropic optimal transport: Toward non-parametric estimation of conditional Brenier maps

Conditional simulation is a fundamental task in statistical modeling: Generate samples from the conditionals given finitely many data points from a joint distribution. One promising approach is to construct conditional Brenier maps, where the components of the map pushforward a reference distribution to conditionals of the target. While many estimators exist, few, if any, come with statistical or algorithmic guarantees. To this end, we propose a non-parametric estimator for conditional Brenier maps based on the computational scalability of \emph{entropic} optimal transport. Our estimator leverages a result of Carlier et al. (2010), which shows that optimal transport maps under a rescaled quadratic cost asymptotically converge to conditional Brenier maps; our estimator is precisely the entropic analogues of these converging maps. We provide heuristic justifications for choosing the scaling parameter in the cost as a function of the number of samples by fully characterizing the Gaussian setting. We conclude by comparing the performance of the estimator to other machine learning and non-parametric approaches on benchmark datasets and Bayesian inference problems.

Dimension reduction via score ratio matching

Gradient-based dimension reduction decreases the cost of Bayesian inference and probabilistic modeling by identifying maximally informative (and informed) low-dimensional projections of the data and parameters, allowing high-dimensional problems to be reformulated as cheaper low-dimensional problems. A broad family of such techniques identify these projections and provide error bounds on the resulting posterior approximations, via eigendecompositions of certain diagnostic matrices. Yet these matrices require gradients or even Hessians of the log-likelihood, excluding the purely data-driven setting and many problems of simulation-based inference. We propose a framework, derived from score-matching, to extend gradient-based dimension reduction to problems where gradients are unavailable. Specifically, we formulate an objective function to directly learn the score ratio function needed to compute the diagnostic matrices, propose a tailored parameterization for the score ratio network, and introduce regularization methods that capitalize on the hypothesized low-dimensional structure. We also introduce a novel algorithm to iteratively identify the low-dimensional reduced basis vectors more accurately with limited data based on eigenvalue deflation methods. We show that our approach outperforms standard score-matching for problems with low-dimensional structure, and demonstrate its effectiveness for PDE-constrained Bayesian inverse problems and conditional generative modeling.