Ricardo Baptista
Large Language Models: A Mathematical Formulation
Jan 21, 2026Abstract:Large language models (LLMs) process and predict sequences containing text to answer questions, and address tasks including document summarization, providing recommendations, writing software and solving quantitative problems. We provide a mathematical framework for LLMs by describing the encoding of text sequences into sequences of tokens, defining the architecture for next-token prediction models, explaining how these models are learned from data, and demonstrating how they are deployed to address a variety of tasks. The mathematical sophistication required to understand this material is not high, and relies on straightforward ideas from information theory, probability and optimization. Nonetheless, the combination of ideas resting on these different components from the mathematical sciences yields a complex algorithmic structure; and this algorithmic structure has demonstrated remarkable empirical successes. The mathematical framework established here provides a platform from which it is possible to formulate and address questions concerning the accuracy, efficiency and robustness of the algorithms that constitute LLMs. The framework also suggests directions for development of modified and new methodologies.
A Mathematical Perspective On Contrastive Learning
May 30, 2025Abstract:Multimodal contrastive learning is a methodology for linking different data modalities; the canonical example is linking image and text data. The methodology is typically framed as the identification of a set of encoders, one for each modality, that align representations within a common latent space. In this work, we focus on the bimodal setting and interpret contrastive learning as the optimization of (parameterized) encoders that define conditional probability distributions, for each modality conditioned on the other, consistent with the available data. This provides a framework for multimodal algorithms such as crossmodal retrieval, which identifies the mode of one of these conditional distributions, and crossmodal classification, which is similar to retrieval but includes a fine-tuning step to make it task specific. The framework we adopt also gives rise to crossmodal generative models. This probabilistic perspective suggests two natural generalizations of contrastive learning: the introduction of novel probabilistic loss functions, and the use of alternative metrics for measuring alignment in the common latent space. We study these generalizations of the classical approach in the multivariate Gaussian setting. In this context we view the latent space identification as a low-rank matrix approximation problem. This allows us to characterize the capabilities of loss functions and alignment metrics to approximate natural statistics, such as conditional means and covariances; doing so yields novel variants on contrastive learning algorithms for specific mode-seeking and for generative tasks. The framework we introduce is also studied through numerical experiments on multivariate Gaussians, the labeled MNIST dataset, and on a data assimilation application arising in oceanography.
Proximal optimal transport divergences
May 17, 2025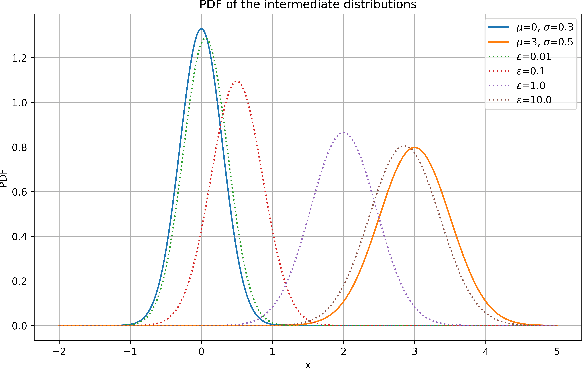
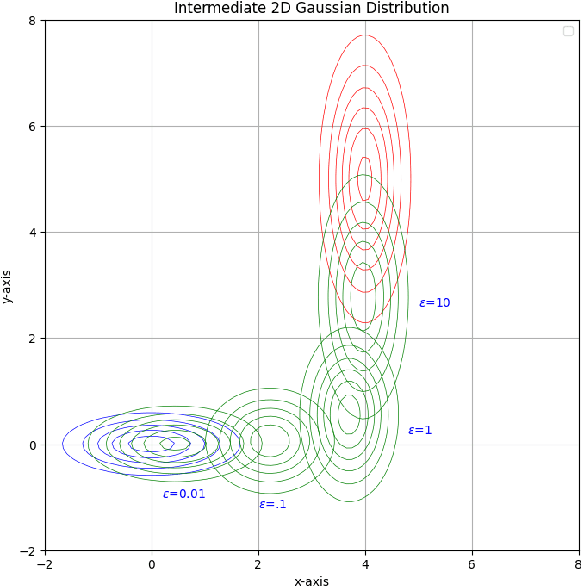
Abstract:We introduce proximal optimal transport divergence, a novel discrepancy measure that interpolates between information divergences and optimal transport distances via an infimal convolution formulation. This divergence provides a principled foundation for optimal transport proximals and proximal optimization methods frequently used in generative modeling. We explore its mathematical properties, including smoothness, boundedness, and computational tractability, and establish connections to primal-dual formulation and adversarial learning. Building on the Benamou-Brenier dynamic formulation of optimal transport cost, we also establish a dynamic formulation for proximal OT divergences. The resulting dynamic formulation is a first order mean-field game whose optimality conditions are governed by a pair of nonlinear partial differential equations, a backward Hamilton-Jacobi and a forward continuity partial differential equations. Our framework generalizes existing approaches while offering new insights and computational tools for generative modeling, distributional optimization, and gradient-based learning in probability spaces.
Learning Enhanced Ensemble Filters
Apr 24, 2025Abstract:The filtering distribution in hidden Markov models evolves according to the law of a mean-field model in state--observation space. The ensemble Kalman filter (EnKF) approximates this mean-field model with an ensemble of interacting particles, employing a Gaussian ansatz for the joint distribution of the state and observation at each observation time. These methods are robust, but the Gaussian ansatz limits accuracy. This shortcoming is addressed by approximating the mean-field evolution using a novel form of neural operator taking probability distributions as input: a Measure Neural Mapping (MNM). A MNM is used to design a novel approach to filtering, the MNM-enhanced ensemble filter (MNMEF), which is defined in both the mean-fieldlimit and for interacting ensemble particle approximations. The ensemble approach uses empirical measures as input to the MNM and is implemented using the set transformer, which is invariant to ensemble permutation and allows for different ensemble sizes. The derivation of methods from a mean-field formulation allows a single parameterization of the algorithm to be deployed at different ensemble sizes. In practice fine-tuning of a small number of parameters, for specific ensemble sizes, further enhances the accuracy of the scheme. The promise of the approach is demonstrated by its superior root-mean-square-error performance relative to leading methods in filtering the Lorenz 96 and Kuramoto-Sivashinsky models.
Learning local neighborhoods of non-Gaussian graphical models: A measure transport approach
Mar 18, 2025



Abstract:Identifying the Markov properties or conditional independencies of a collection of random variables is a fundamental task in statistics for modeling and inference. Existing approaches often learn the structure of a probabilistic graphical model, which encodes these dependencies, by assuming that the variables follow a distribution with a simple parametric form. Moreover, the computational cost of many algorithms scales poorly for high-dimensional distributions, as they need to estimate all the edges in the graph simultaneously. In this work, we propose a scalable algorithm to infer the conditional independence relationships of each variable by exploiting the local Markov property. The proposed method, named Localized Sparsity Identification for Non-Gaussian Distributions (L-SING), estimates the graph by using flexible classes of transport maps to represent the conditional distribution for each variable. We show that L-SING includes existing approaches, such as neighborhood selection with Lasso, as a special case. We demonstrate the effectiveness of our algorithm in both Gaussian and non-Gaussian settings by comparing it to existing methods. Lastly, we show the scalability of the proposed approach by applying it to high-dimensional non-Gaussian examples, including a biological dataset with more than 150 variables.
Solving Roughly Forced Nonlinear PDEs via Misspecified Kernel Methods and Neural Networks
Jan 29, 2025Abstract:We consider the use of Gaussian Processes (GPs) or Neural Networks (NNs) to numerically approximate the solutions to nonlinear partial differential equations (PDEs) with rough forcing or source terms, which commonly arise as pathwise solutions to stochastic PDEs. Kernel methods have recently been generalized to solve nonlinear PDEs by approximating their solutions as the maximum a posteriori estimator of GPs that are conditioned to satisfy the PDE at a finite set of collocation points. The convergence and error guarantees of these methods, however, rely on the PDE being defined in a classical sense and its solution possessing sufficient regularity to belong to the associated reproducing kernel Hilbert space. We propose a generalization of these methods to handle roughly forced nonlinear PDEs while preserving convergence guarantees with an oversmoothing GP kernel that is misspecified relative to the true solution's regularity. This is achieved by conditioning a regular GP to satisfy the PDE with a modified source term in a weak sense (when integrated against a finite number of test functions). This is equivalent to replacing the empirical $L^2$-loss on the PDE constraint by an empirical negative-Sobolev norm. We further show that this loss function can be used to extend physics-informed neural networks (PINNs) to stochastic equations, thereby resulting in a new NN-based variant termed Negative Sobolev Norm-PINN (NeS-PINN).
Memorization and Regularization in Generative Diffusion Models
Jan 27, 2025



Abstract:Diffusion models have emerged as a powerful framework for generative modeling. At the heart of the methodology is score matching: learning gradients of families of log-densities for noisy versions of the data distribution at different scales. When the loss function adopted in score matching is evaluated using empirical data, rather than the population loss, the minimizer corresponds to the score of a time-dependent Gaussian mixture. However, use of this analytically tractable minimizer leads to data memorization: in both unconditioned and conditioned settings, the generative model returns the training samples. This paper contains an analysis of the dynamical mechanism underlying memorization. The analysis highlights the need for regularization to avoid reproducing the analytically tractable minimizer; and, in so doing, lays the foundations for a principled understanding of how to regularize. Numerical experiments investigate the properties of: (i) Tikhonov regularization; (ii) regularization designed to promote asymptotic consistency; and (iii) regularizations induced by under-parameterization of a neural network or by early stopping when training a neural network. These experiments are evaluated in the context of memorization, and directions for future development of regularization are highlighted.
Expected Information Gain Estimation via Density Approximations: Sample Allocation and Dimension Reduction
Nov 13, 2024Abstract:Computing expected information gain (EIG) from prior to posterior (equivalently, mutual information between candidate observations and model parameters or other quantities of interest) is a fundamental challenge in Bayesian optimal experimental design. We formulate flexible transport-based schemes for EIG estimation in general nonlinear/non-Gaussian settings, compatible with both standard and implicit Bayesian models. These schemes are representative of two-stage methods for estimating or bounding EIG using marginal and conditional density estimates. In this setting, we analyze the optimal allocation of samples between training (density estimation) and approximation of the outer prior expectation. We show that with this optimal sample allocation, the MSE of the resulting EIG estimator converges more quickly than that of a standard nested Monte Carlo scheme. We then address the estimation of EIG in high dimensions, by deriving gradient-based upper bounds on the mutual information lost by projecting the parameters and/or observations to lower-dimensional subspaces. Minimizing these upper bounds yields projectors and hence low-dimensional EIG approximations that outperform approximations obtained via other linear dimension reduction schemes. Numerical experiments on a PDE-constrained Bayesian inverse problem also illustrate a favorable trade-off between dimension truncation and the modeling of non-Gaussianity, when estimating EIG from finite samples in high dimensions.
Conditional simulation via entropic optimal transport: Toward non-parametric estimation of conditional Brenier maps
Nov 11, 2024



Abstract:Conditional simulation is a fundamental task in statistical modeling: Generate samples from the conditionals given finitely many data points from a joint distribution. One promising approach is to construct conditional Brenier maps, where the components of the map pushforward a reference distribution to conditionals of the target. While many estimators exist, few, if any, come with statistical or algorithmic guarantees. To this end, we propose a non-parametric estimator for conditional Brenier maps based on the computational scalability of \emph{entropic} optimal transport. Our estimator leverages a result of Carlier et al. (2010), which shows that optimal transport maps under a rescaled quadratic cost asymptotically converge to conditional Brenier maps; our estimator is precisely the entropic analogues of these converging maps. We provide heuristic justifications for choosing the scaling parameter in the cost as a function of the number of samples by fully characterizing the Gaussian setting. We conclude by comparing the performance of the estimator to other machine learning and non-parametric approaches on benchmark datasets and Bayesian inference problems.
Dimension reduction via score ratio matching
Oct 25, 2024

Abstract:Gradient-based dimension reduction decreases the cost of Bayesian inference and probabilistic modeling by identifying maximally informative (and informed) low-dimensional projections of the data and parameters, allowing high-dimensional problems to be reformulated as cheaper low-dimensional problems. A broad family of such techniques identify these projections and provide error bounds on the resulting posterior approximations, via eigendecompositions of certain diagnostic matrices. Yet these matrices require gradients or even Hessians of the log-likelihood, excluding the purely data-driven setting and many problems of simulation-based inference. We propose a framework, derived from score-matching, to extend gradient-based dimension reduction to problems where gradients are unavailable. Specifically, we formulate an objective function to directly learn the score ratio function needed to compute the diagnostic matrices, propose a tailored parameterization for the score ratio network, and introduce regularization methods that capitalize on the hypothesized low-dimensional structure. We also introduce a novel algorithm to iteratively identify the low-dimensional reduced basis vectors more accurately with limited data based on eigenvalue deflation methods. We show that our approach outperforms standard score-matching for problems with low-dimensional structure, and demonstrate its effectiveness for PDE-constrained Bayesian inverse problems and conditional generative modeling.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge