Convergence Rates for Learning Pseudo-Differential Operators

This paper establishes convergence rates for learning elliptic pseudo-differential operators, a fundamental operator class in partial differential equations and mathematical physics. In a wavelet-Galerkin framework, we formulate learning over this class as a structured infinite-dimensional regression problem with multiscale sparsity. Building on this structure, we propose a sparse, data- and computation-efficient estimator, which leverages a novel matrix compression scheme tailored to the learning task and a nested-support strategy to balance approximation and estimation errors. In addition to obtaining convergence rates for the estimator, we show that the learned operator induces an efficient and stable Galerkin solver whose numerical error matches its statistical accuracy. Our results therefore contribute to bringing together operator learning, data-driven solvers, and wavelet methods in scientific computing.

Bayesian Optimization on Networks

This paper studies optimization on networks modeled as metric graphs. Motivated by applications where the objective function is expensive to evaluate or only available as a black box, we develop Bayesian optimization algorithms that sequentially update a Gaussian process surrogate model of the objective to guide the acquisition of query points. To ensure that the surrogates are tailored to the network's geometry, we adopt Whittle-Mat\'ern Gaussian process prior models defined via stochastic partial differential equations on metric graphs. In addition to establishing regret bounds for optimizing sufficiently smooth objective functions, we analyze the practical case in which the smoothness of the objective is unknown and the Whittle-Mat\'ern prior is represented using finite elements. Numerical results demonstrate the effectiveness of our algorithms for optimizing benchmark objective functions on a synthetic metric graph and for Bayesian inversion via maximum a posteriori estimation on a telecommunication network.

Functional Multi-Reference Alignment via Deconvolution

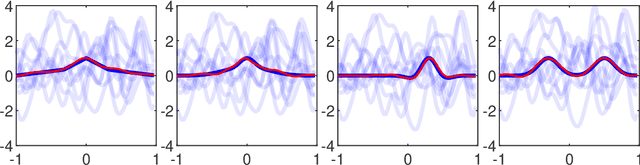
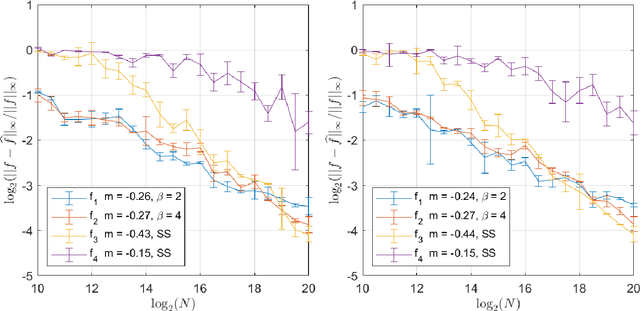
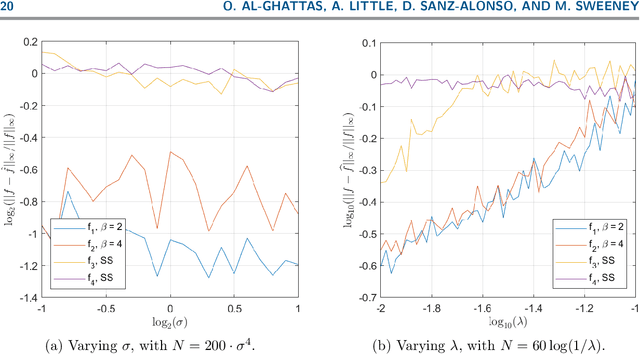
This paper studies the multi-reference alignment (MRA) problem of estimating a signal function from shifted, noisy observations. Our functional formulation reveals a new connection between MRA and deconvolution: the signal can be estimated from second-order statistics via Kotlarski's formula, an important identification result in deconvolution with replicated measurements. To design our MRA algorithms, we extend Kotlarski's formula to general dimension and study the estimation of signals with vanishing Fourier transform, thus also contributing to the deconvolution literature. We validate our deconvolution approach to MRA through both theory and numerical experiments.

Long-time accuracy of ensemble Kalman filters for chaotic and machine-learned dynamical systems

Filtering is concerned with online estimation of the state of a dynamical system from partial and noisy observations. In applications where the state is high dimensional, ensemble Kalman filters are often the method of choice. This paper establishes long-time accuracy of ensemble Kalman filters. We introduce conditions on the dynamics and the observations under which the estimation error remains small in the long-time horizon. Our theory covers a wide class of partially-observed chaotic dynamical systems, which includes the Navier-Stokes equations and Lorenz models. In addition, we prove long-time accuracy of ensemble Kalman filters with surrogate dynamics, thus validating the use of machine-learned forecast models in ensemble data assimilation.

Inverse Problems and Data Assimilation: A Machine Learning Approach

The aim of these notes is to demonstrate the potential for ideas in machine learning to impact on the fields of inverse problems and data assimilation. The perspective is one that is primarily aimed at researchers from inverse problems and/or data assimilation who wish to see a mathematical presentation of machine learning as it pertains to their fields. As a by-product, we include a succinct mathematical treatment of various topics in machine learning.

Data Assimilation with Machine Learning Surrogate Models: A Case Study with FourCastNet

Modern data-driven surrogate models for weather forecasting provide accurate short-term predictions but inaccurate and nonphysical long-term forecasts. This paper investigates online weather prediction using machine learning surrogates supplemented with partial and noisy observations. We empirically demonstrate and theoretically justify that, despite the long-time instability of the surrogates and the sparsity of the observations, filtering estimates can remain accurate in the long-time horizon. As a case study, we integrate FourCastNet, a state-of-the-art weather surrogate model, within a variational data assimilation framework using partial, noisy ERA5 data. Our results show that filtering estimates remain accurate over a year-long assimilation window and provide effective initial conditions for forecasting tasks, including extreme event prediction.

Bayesian Optimization with Noise-Free Observations: Improved Regret Bounds via Random Exploration

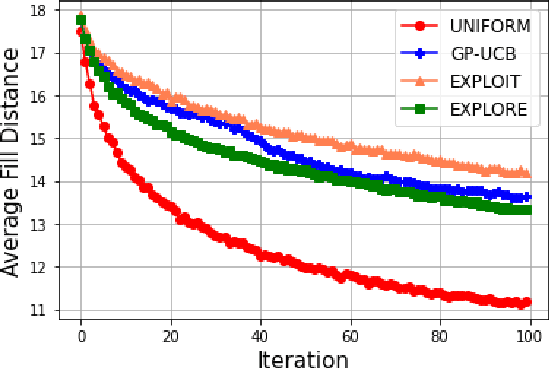
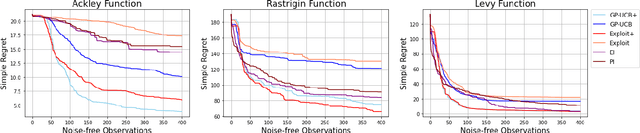
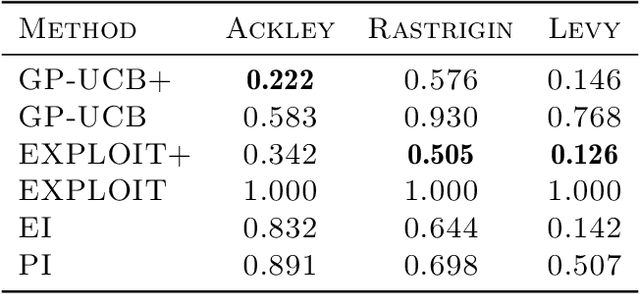
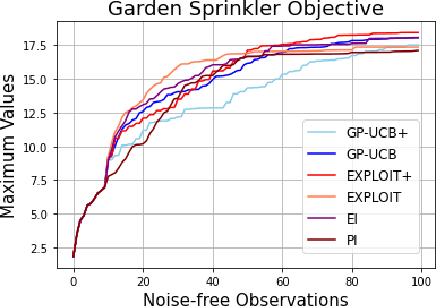
This paper studies Bayesian optimization with noise-free observations. We introduce new algorithms rooted in scattered data approximation that rely on a random exploration step to ensure that the fill-distance of query points decays at a near-optimal rate. Our algorithms retain the ease of implementation of the classical GP-UCB algorithm and satisfy cumulative regret bounds that nearly match those conjectured in arXiv:2002.05096, hence solving a COLT open problem. Furthermore, the new algorithms outperform GP-UCB and other popular Bayesian optimization strategies in several examples.

Gaussian Process Regression under Computational and Epistemic Misspecification

Gaussian process regression is a classical kernel method for function estimation and data interpolation. In large data applications, computational costs can be reduced using low-rank or sparse approximations of the kernel. This paper investigates the effect of such kernel approximations on the interpolation error. We introduce a unified framework to analyze Gaussian process regression under important classes of computational misspecification: Karhunen-Lo\`eve expansions that result in low-rank kernel approximations, multiscale wavelet expansions that induce sparsity in the covariance matrix, and finite element representations that induce sparsity in the precision matrix. Our theory also accounts for epistemic misspecification in the choice of kernel parameters.

Reduced-Order Autodifferentiable Ensemble Kalman Filters

This paper introduces a computational framework to reconstruct and forecast a partially observed state that evolves according to an unknown or expensive-to-simulate dynamical system. Our reduced-order autodifferentiable ensemble Kalman filters (ROAD-EnKFs) learn a latent low-dimensional surrogate model for the dynamics and a decoder that maps from the latent space to the state space. The learned dynamics and decoder are then used within an ensemble Kalman filter to reconstruct and forecast the state. Numerical experiments show that if the state dynamics exhibit a hidden low-dimensional structure, ROAD-EnKFs achieve higher accuracy at lower computational cost compared to existing methods. If such structure is not expressed in the latent state dynamics, ROAD-EnKFs achieve similar accuracy at lower cost, making them a promising approach for surrogate state reconstruction and forecasting.

Non-Asymptotic Analysis of Ensemble Kalman Updates: Effective Dimension and Localization

Many modern algorithms for inverse problems and data assimilation rely on ensemble Kalman updates to blend prior predictions with observed data. Ensemble Kalman methods often perform well with a small ensemble size, which is essential in applications where generating each particle is costly. This paper develops a non-asymptotic analysis of ensemble Kalman updates that rigorously explains why a small ensemble size suffices if the prior covariance has moderate effective dimension due to fast spectrum decay or approximate sparsity. We present our theory in a unified framework, comparing several implementations of ensemble Kalman updates that use perturbed observations, square root filtering, and localization. As part of our analysis, we develop new dimension-free covariance estimation bounds for approximately sparse matrices that may be of independent interest.