Learning Enhanced Ensemble Filters

The filtering distribution in hidden Markov models evolves according to the law of a mean-field model in state--observation space. The ensemble Kalman filter (EnKF) approximates this mean-field model with an ensemble of interacting particles, employing a Gaussian ansatz for the joint distribution of the state and observation at each observation time. These methods are robust, but the Gaussian ansatz limits accuracy. This shortcoming is addressed by approximating the mean-field evolution using a novel form of neural operator taking probability distributions as input: a Measure Neural Mapping (MNM). A MNM is used to design a novel approach to filtering, the MNM-enhanced ensemble filter (MNMEF), which is defined in both the mean-fieldlimit and for interacting ensemble particle approximations. The ensemble approach uses empirical measures as input to the MNM and is implemented using the set transformer, which is invariant to ensemble permutation and allows for different ensemble sizes. The derivation of methods from a mean-field formulation allows a single parameterization of the algorithm to be deployed at different ensemble sizes. In practice fine-tuning of a small number of parameters, for specific ensemble sizes, further enhances the accuracy of the scheme. The promise of the approach is demonstrated by its superior root-mean-square-error performance relative to leading methods in filtering the Lorenz 96 and Kuramoto-Sivashinsky models.

Nesterov Acceleration for Ensemble Kalman Inversion and Variants

Ensemble Kalman inversion (EKI) is a derivative-free, particle-based optimization method for solving inverse problems. It can be shown that EKI approximates a gradient flow, which allows the application of methods for accelerating gradient descent. Here, we show that Nesterov acceleration is effective in speeding up the reduction of the EKI cost function on a variety of inverse problems. We also implement Nesterov acceleration for two EKI variants, unscented Kalman inversion and ensemble transform Kalman inversion. Our specific implementation takes the form of a particle-level nudge that is demonstrably simple to couple in a black-box fashion with any existing EKI variant algorithms, comes with no additional computational expense, and with no additional tuning hyperparameters. This work shows a pathway for future research to translate advances in gradient-based optimization into advances in gradient-free Kalman optimization.

Inverse Problems and Data Assimilation: A Machine Learning Approach

The aim of these notes is to demonstrate the potential for ideas in machine learning to impact on the fields of inverse problems and data assimilation. The perspective is one that is primarily aimed at researchers from inverse problems and/or data assimilation who wish to see a mathematical presentation of machine learning as it pertains to their fields. As a by-product, we include a succinct mathematical treatment of various topics in machine learning.

Learning Optimal Filters Using Variational Inference

Filtering-the task of estimating the conditional distribution of states of a dynamical system given partial, noisy, observations-is important in many areas of science and engineering, including weather and climate prediction. However, the filtering distribution is generally intractable to obtain for high-dimensional, nonlinear systems. Filters used in practice, such as the ensemble Kalman filter (EnKF), are biased for nonlinear systems and have numerous tuning parameters. Here, we present a framework for learning a parameterized analysis map-the map that takes a forecast distribution and observations to the filtering distribution-using variational inference. We show that this methodology can be used to learn gain matrices for filtering linear and nonlinear dynamical systems, as well as inflation and localization parameters for an EnKF. Future work will apply this framework to learn new filtering algorithms.

Deep learning-enhanced ensemble-based data assimilation for high-dimensional nonlinear dynamical systems

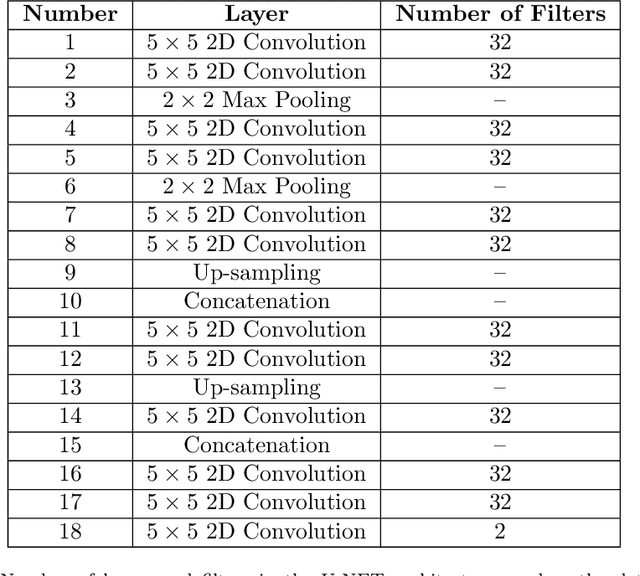
Data assimilation (DA) is a key component of many forecasting models in science and engineering. DA allows one to estimate better initial conditions using an imperfect dynamical model of the system and noisy/sparse observations available from the system. Ensemble Kalman filter (EnKF) is a DA algorithm that is widely used in applications involving high-dimensional nonlinear dynamical systems. However, EnKF requires evolving large ensembles of forecasts using the dynamical model of the system. This often becomes computationally intractable, especially when the number of states of the system is very large, e.g., for weather prediction. With small ensembles, the estimated background error covariance matrix in the EnKF algorithm suffers from sampling error, leading to an erroneous estimate of the analysis state (initial condition for the next forecast cycle). In this work, we propose hybrid ensemble Kalman filter (H-EnKF), which is applied to a two-layer quasi-geostrophic flow system as a test case. This framework utilizes a pre-trained deep learning-based data-driven surrogate that inexpensively generates and evolves a large data-driven ensemble of the states of the system to accurately compute the background error covariance matrix with less sampling error. The H-EnKF framework estimates a better initial condition without the need for any ad-hoc localization strategies. H-EnKF can be extended to any ensemble-based DA algorithm, e.g., particle filters, which are currently difficult to use for high dimensional systems.

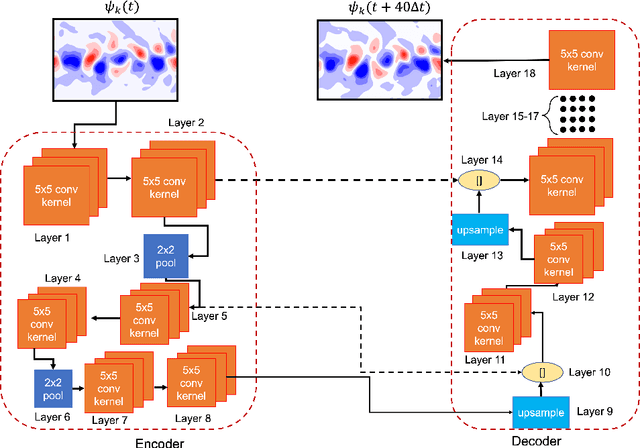
Towards physically consistent data-driven weather forecasting: Integrating data assimilation with equivariance-preserving deep spatial transformers

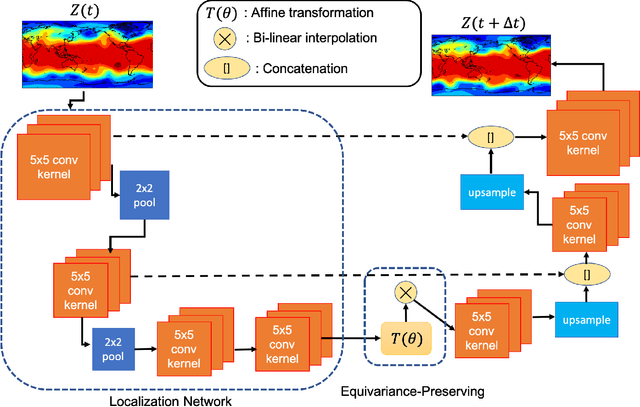
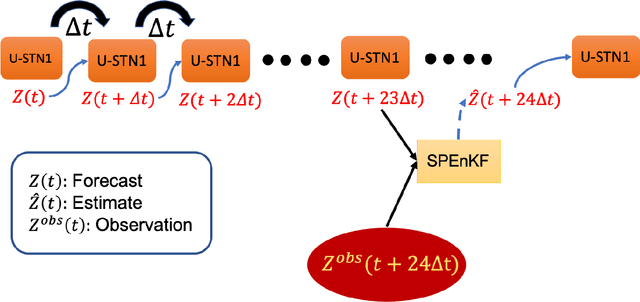
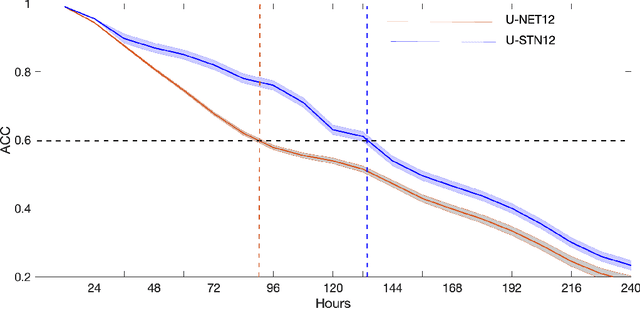
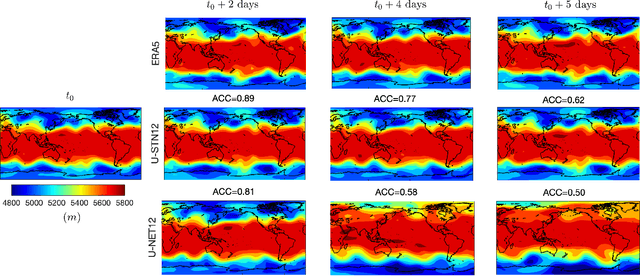
There is growing interest in data-driven weather prediction (DDWP), for example using convolutional neural networks such as U-NETs that are trained on data from models or reanalysis. Here, we propose 3 components to integrate with commonly used DDWP models in order to improve their physical consistency and forecast accuracy. These components are 1) a deep spatial transformer added to the latent space of the U-NETs to preserve a property called equivariance, which is related to correctly capturing rotations and scalings of features in spatio-temporal data, 2) a data-assimilation (DA) algorithm to ingest noisy observations and improve the initial conditions for next forecasts, and 3) a multi-time-step algorithm, which combines forecasts from DDWP models with different time steps through DA, improving the accuracy of forecasts at short intervals. To show the benefit/feasibility of each component, we use geopotential height at 500~hPa (Z500) from ERA5 reanalysis and examine the short-term forecast accuracy of specific setups of the DDWP framework. Results show that the equivariance-preserving networks (U-STNs) clearly outperform the U-NETs, for example improving the forecast skill by $45\%$. Using a sigma-point ensemble Kalman (SPEnKF) algorithm for DA and U-STN as the forward model, we show that stable, accurate DA cycles are achieved even with high observation noise. The DDWP+DA framework substantially benefits from large ($O(1000)$) ensembles that are inexpensively generated with the data-driven forward model in each DA cycle. The multi-time-step DDWP+DA framework also shows promises, e.g., it reduces the average error by factors of 2-3.