Pedram Hassanzadeh
Decision-oriented benchmarking to transform AI weather forecast access: Application to the Indian monsoon
Feb 03, 2026Abstract:Artificial intelligence weather prediction (AIWP) models now often outperform traditional physics-based models on common metrics while requiring orders-of-magnitude less computing resources and time. Open-access AIWP models thus hold promise as transformational tools for helping low- and middle-income populations make decisions in the face of high-impact weather shocks. Yet, current approaches to evaluating AIWP models focus mainly on aggregated meteorological metrics without considering local stakeholders' needs in decision-oriented, operational frameworks. Here, we introduce such a framework that connects meteorology, AI, and social sciences. As an example, we apply it to the 150-year-old problem of Indian monsoon forecasting, focusing on benefits to rain-fed agriculture, which is highly susceptible to climate change. AIWP models skillfully predict an agriculturally relevant onset index at regional scales weeks in advance when evaluated out-of-sample using deterministic and probabilistic metrics. This framework informed a government-led effort in 2025 to send 38 million Indian farmers AI-based monsoon onset forecasts, which captured an unusual weeks-long pause in monsoon progression. This decision-oriented benchmarking framework provides a key component of a blueprint for harnessing the power of AIWP models to help large vulnerable populations adapt to weather shocks in the face of climate variability and change.
AI-boosted rare event sampling to characterize extreme weather
Oct 31, 2025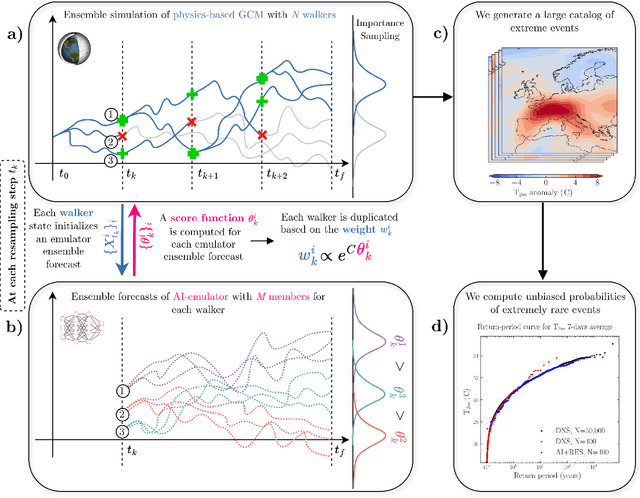
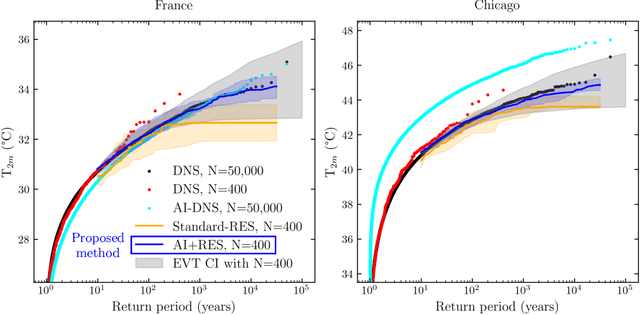
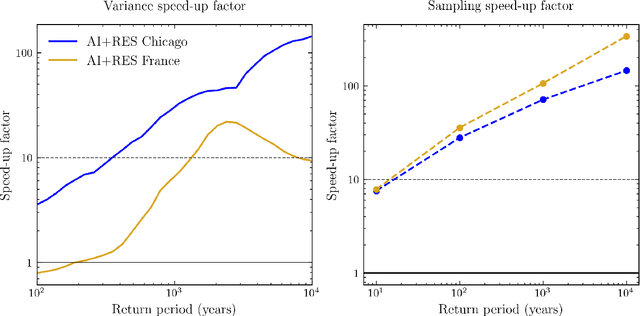
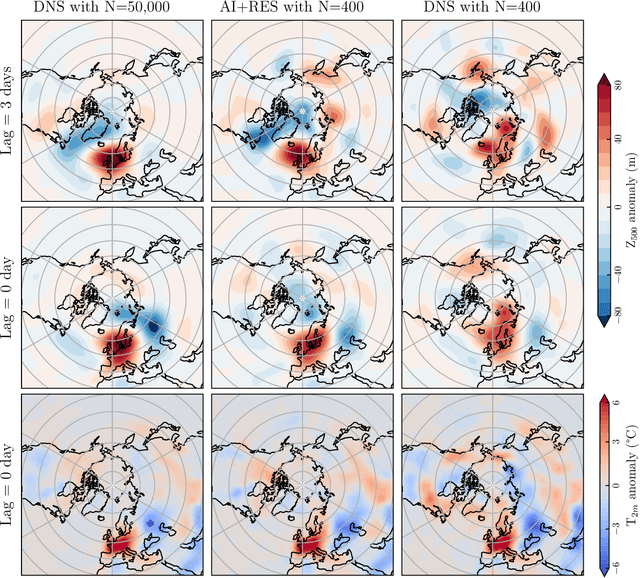
Abstract:Assessing the frequency and intensity of extreme weather events, and understanding how climate change affects them, is crucial for developing effective adaptation and mitigation strategies. However, observational datasets are too short and physics-based global climate models (GCMs) are too computationally expensive to obtain robust statistics for the rarest, yet most impactful, extreme events. AI-based emulators have shown promise for predictions at weather and even climate timescales, but they struggle on extreme events with few or no examples in their training dataset. Rare event sampling (RES) algorithms have previously demonstrated success for some extreme events, but their performance depends critically on a hard-to-identify "score function", which guides efficient sampling by a GCM. Here, we develop a novel algorithm, AI+RES, which uses ensemble forecasts of an AI weather emulator as the score function to guide highly efficient resampling of the GCM and generate robust (physics-based) extreme weather statistics and associated dynamics at 30-300x lower cost. We demonstrate AI+RES on mid-latitude heatwaves, a challenging test case requiring a score function with predictive skill many days in advance. AI+RES, which synergistically integrates AI, RES, and GCMs, offers a powerful, scalable tool for studying extreme events in climate science, as well as other disciplines in science and engineering where rare events and AI emulators are active areas of research.
Benchmarking atmospheric circulation variability in an AI emulator, ACE2, and a hybrid model, NeuralGCM
Oct 06, 2025Abstract:Physics-based atmosphere-land models with prescribed sea surface temperature have notable successes but also biases in their ability to represent atmospheric variability compared to observations. Recently, AI emulators and hybrid models have emerged with the potential to overcome these biases, but still require systematic evaluation against metrics grounded in fundamental atmospheric dynamics. Here, we evaluate the representation of four atmospheric variability benchmarking metrics in a fully data-driven AI emulator (ACE2-ERA5) and hybrid model (NeuralGCM). The hybrid model and emulator can capture the spectra of large-scale tropical waves and extratropical eddy-mean flow interactions, including critical levels. However, both struggle to capture the timescales associated with quasi-biennial oscillation (QBO, $\sim 28$ months) and Southern annular mode propagation ($\sim 150$ days). These dynamical metrics serve as an initial benchmarking tool to inform AI model development and understand their limitations, which may be essential for out-of-distribution applications (e.g., extrapolating to unseen climates).
Hierarchical Implicit Neural Emulators
Jun 05, 2025Abstract:Neural PDE solvers offer a powerful tool for modeling complex dynamical systems, but often struggle with error accumulation over long time horizons and maintaining stability and physical consistency. We introduce a multiscale implicit neural emulator that enhances long-term prediction accuracy by conditioning on a hierarchy of lower-dimensional future state representations. Drawing inspiration from the stability properties of numerical implicit time-stepping methods, our approach leverages predictions several steps ahead in time at increasing compression rates for next-timestep refinements. By actively adjusting the temporal downsampling ratios, our design enables the model to capture dynamics across multiple granularities and enforce long-range temporal coherence. Experiments on turbulent fluid dynamics show that our method achieves high short-term accuracy and produces long-term stable forecasts, significantly outperforming autoregressive baselines while adding minimal computational overhead.
Fourier analysis of the physics of transfer learning for data-driven subgrid-scale models of ocean turbulence
Apr 21, 2025Abstract:Transfer learning (TL) is a powerful tool for enhancing the performance of neural networks (NNs) in applications such as weather and climate prediction and turbulence modeling. TL enables models to generalize to out-of-distribution data with minimal training data from the new system. In this study, we employ a 9-layer convolutional NN to predict the subgrid forcing in a two-layer ocean quasi-geostrophic system and examine which metrics best describe its performance and generalizability to unseen dynamical regimes. Fourier analysis of the NN kernels reveals that they learn low-pass, Gabor, and high-pass filters, regardless of whether the training data are isotropic or anisotropic. By analyzing the activation spectra, we identify why NNs fail to generalize without TL and how TL can overcome these limitations: the learned weights and biases from one dataset underestimate the out-of-distribution sample spectra as they pass through the network, leading to an underestimation of output spectra. By re-training only one layer with data from the target system, this underestimation is corrected, enabling the NN to produce predictions that match the target spectra. These findings are broadly applicable to data-driven parameterization of dynamical systems.
Can AI weather models predict out-of-distribution gray swan tropical cyclones?
Oct 19, 2024



Abstract:Predicting gray swan weather extremes, which are possible but so rare that they are absent from the training dataset, is a major concern for AI weather/climate models. An important open question is whether AI models can extrapolate from weaker weather events present in the training set to stronger, unseen weather extremes. To test this, we train independent versions of the AI model FourCastNet on the 1979-2015 ERA5 dataset with all data, or with Category 3-5 tropical cyclones (TCs) removed, either globally or only over the North Atlantic or Western Pacific basin. We then test these versions of FourCastNet on 2018-2023 Category 5 TCs (gray swans). All versions yield similar accuracy for global weather, but the one trained without Category 3-5 TCs cannot accurately forecast Category 5 TCs, indicating that these models cannot extrapolate from weaker storms. The versions trained without Category 3-5 TCs in one basin show some skill forecasting Category 5 TCs in that basin, suggesting that FourCastNet can generalize across tropical basins. This is encouraging and surprising because regional information is implicitly encoded in inputs. No version satisfies gradient-wind balance, implying that enforcing such physical constraints may not improve generalizability to gray swans. Given that current state-of-the-art AI weather/climate models have similar learning strategies, we expect our findings to apply to other models and extreme events. Our work demonstrates that novel learning strategies are needed for AI weather/climate models to provide early warning or estimated statistics for the rarest, most impactful weather extremes.
On the importance of learning non-local dynamics for stable data-driven climate modeling: A 1D gravity wave-QBO testbed
Jul 07, 2024Abstract:Machine learning (ML) techniques, especially neural networks (NNs), have shown promise in learning subgrid-scale (SGS) parameterizations for climate modeling. However, a major problem with data-driven parameterizations, particularly those learned with supervised algorithms, is instability when integrated with numerical solvers of large-scale processes. Current remedies are often ad-hoc and lack a theoretical foundation. Here, we combine ML theory and climate physics to address a source of instability in NN-based parameterization. We demonstrate the importance of learning spatially non-local dynamics using a 1D model of the quasi-biennial oscillation (QBO) with gravity wave (GW) parameterization as a testbed. While common offline metrics fail to identify shortcomings in learning non-local dynamics, we show that the receptive field (RF)-the region of the input an NN uses to predict an output-can identify instability a-priori. We find that NN-based parameterizations that seem to accurately predict GW forcings from wind profiles ($\mathbf{R^2 \approx 0.99}$) cause unstable simulations when RF is too small to capture the non-local dynamics, while NNs of the same size but large-enough RF are stable. Some architectures, e.g., Fourier neural operators, have inherently large RF. We also demonstrate that learning non-local dynamics can be crucial for the stability and accuracy of a data-driven spatiotemporal emulator of the entire zonal wind field. Given the ubiquity of non-local dynamics in the climate system, we expect the use of effective RF, which can be computed for any NN architecture, to be important for many applications. This work highlights the need to integrate ML theory with physics for designing/analyzing data-driven algorithms for weather/climate modeling.
Extreme Event Prediction with Multi-agent Reinforcement Learning-based Parametrization of Atmospheric and Oceanic Turbulence
Dec 01, 2023


Abstract:Global climate models (GCMs) are the main tools for understanding and predicting climate change. However, due to limited numerical resolutions, these models suffer from major structural uncertainties; e.g., they cannot resolve critical processes such as small-scale eddies in atmospheric and oceanic turbulence. Thus, such small-scale processes have to be represented as a function of the resolved scales via closures (parametrization). The accuracy of these closures is particularly important for capturing climate extremes. Traditionally, such closures are based on heuristics and simplifying assumptions about the unresolved physics. Recently, supervised-learned closures, trained offline on high-fidelity data, have been shown to outperform the classical physics-based closures. However, this approach requires a significant amount of high-fidelity training data and can also lead to instabilities. Reinforcement learning is emerging as a potent alternative for developing such closures as it requires only low-order statistics and leads to stable closures. In Scientific Multi-Agent Reinforcement Learning (SMARL) computational elements serve a dual role of discretization points and learning agents. We leverage SMARL and fundamentals of turbulence physics to learn closures for prototypes of atmospheric and oceanic turbulence. The policy is trained using only the enstrophy spectrum, which is nearly invariant and can be estimated from a few high-fidelity samples (these few samples are far from enough for supervised/offline learning). We show that these closures lead to stable low-resolution simulations that, at a fraction of the cost, can reproduce the high-fidelity simulations' statistics, including the tails of the probability density functions. The results demonstrate the high potential of SMARL for closure modeling for GCMs, especially in the regime of scarce data and indirect observations.
Learning Closed-form Equations for Subgrid-scale Closures from High-fidelity Data: Promises and Challenges
Jun 08, 2023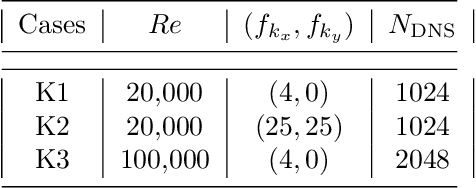
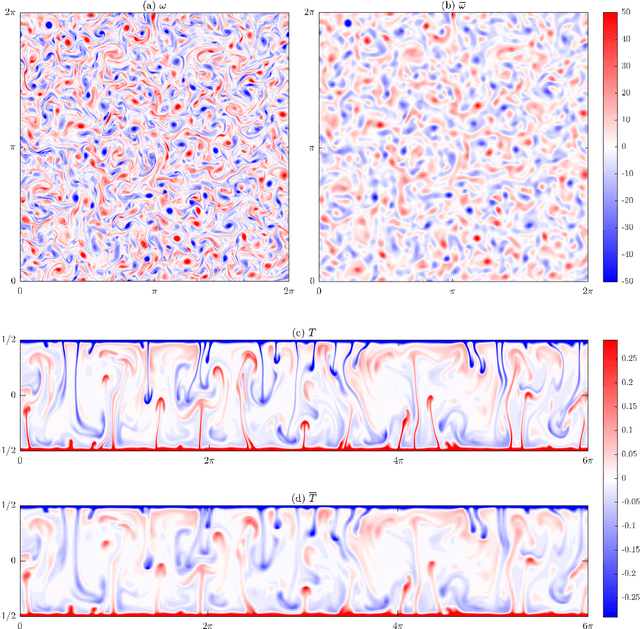
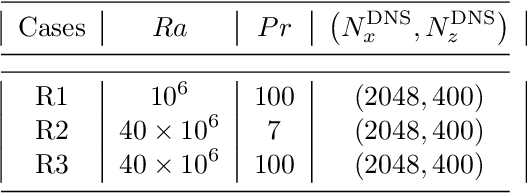
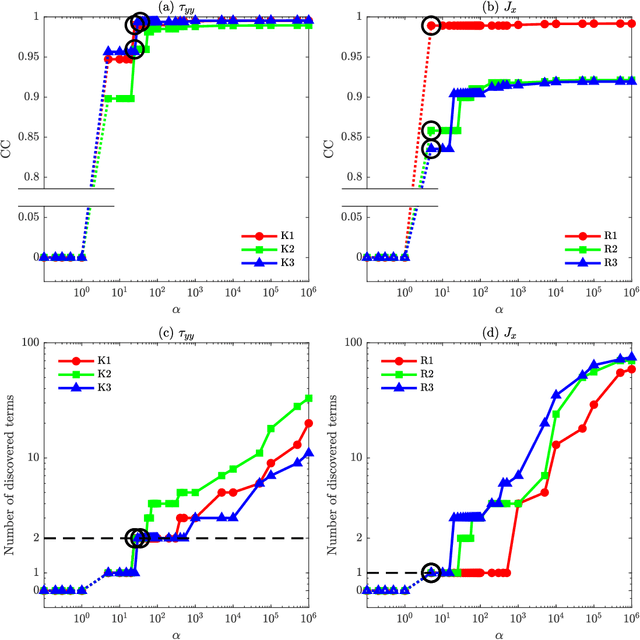
Abstract:There is growing interest in discovering interpretable, closed-form equations for subgrid-scale (SGS) closures/parameterizations of complex processes in Earth system. Here, we apply a common equation-discovery technique with expansive libraries to learn closures from filtered direct numerical simulations of 2D forced turbulence and Rayleigh-B\'enard convection (RBC). Across common filters, we robustly discover closures of the same form for momentum and heat fluxes. These closures depend on nonlinear combinations of gradients of filtered variables (velocity, temperature), with constants that are independent of the fluid/flow properties and only depend on filter type/size. We show that these closures are the nonlinear gradient model (NGM), which is derivable analytically using Taylor-series expansions. In fact, we suggest that with common (physics-free) equation-discovery algorithms, regardless of the system/physics, discovered closures are always consistent with the Taylor-series. Like previous studies, we find that large-eddy simulations with NGM closures are unstable, despite significant similarities between the true and NGM-predicted fluxes (pattern correlations $> 0.95$). We identify two shortcomings as reasons for these instabilities: in 2D, NGM produces zero kinetic energy transfer between resolved and subgrid scales, lacking both diffusion and backscattering. In RBC, backscattering of potential energy is poorly predicted. Moreover, we show that SGS fluxes diagnosed from data, presumed the "truth" for discovery, depend on filtering procedures and are not unique. Accordingly, to learn accurate, stable closures from high-fidelity data in future work, we propose several ideas around using physics-informed libraries, loss functions, and metrics. These findings are relevant beyond turbulence to closure modeling of any multi-scale system.
Long-term instabilities of deep learning-based digital twins of the climate system: The cause and a solution
Apr 14, 2023Abstract:Long-term stability is a critical property for deep learning-based data-driven digital twins of the Earth system. Such data-driven digital twins enable sub-seasonal and seasonal predictions of extreme environmental events, probabilistic forecasts, that require a large number of ensemble members, and computationally tractable high-resolution Earth system models where expensive components of the models can be replaced with cheaper data-driven surrogates. Owing to computational cost, physics-based digital twins, though long-term stable, are intractable for real-time decision-making. Data-driven digital twins offer a cheaper alternative to them and can provide real-time predictions. However, such digital twins can only provide short-term forecasts accurately since they become unstable when time-integrated beyond 20 days. Currently, the cause of the instabilities is unknown, and the methods that are used to improve their stability horizons are ad-hoc and lack rigorous theory. In this paper, we reveal that the universal causal mechanism for these instabilities in any turbulent flow is due to \textit{spectral bias} wherein, \textit{any} deep learning architecture is biased to learn only the large-scale dynamics and ignores the small scales completely. We further elucidate how turbulence physics and the absence of convergence in deep learning-based time-integrators amplify this bias leading to unstable error propagation. Finally, using the quasigeostrophic flow and ECMWF Reanalysis data as test cases, we bridge the gap between deep learning theory and fundamental numerical analysis to propose one mitigative solution to such instabilities. We develop long-term stable data-driven digital twins for the climate system and demonstrate accurate short-term forecasts, and hundreds of years of long-term stable time-integration with accurate mean and variability.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge