Samudra: An AI Global Ocean Emulator for Climate

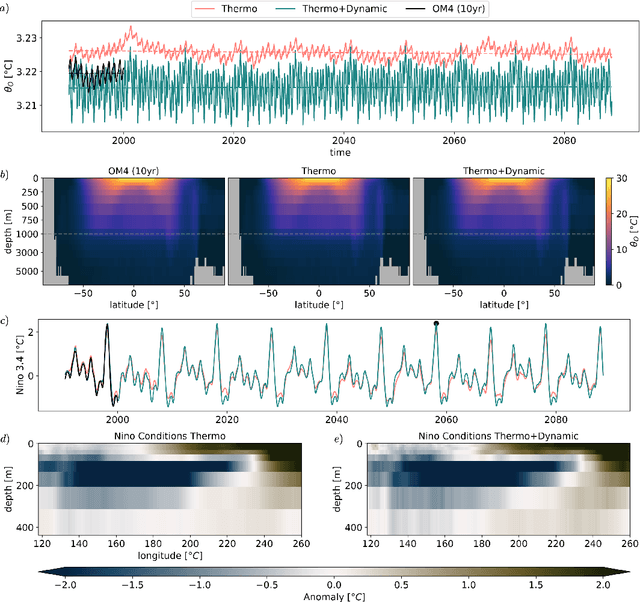
AI emulators for forecasting have emerged as powerful tools that can outperform conventional numerical predictions. The next frontier is to build emulators for long-term climate projections with robust skill across a wide range of spatiotemporal scales, a particularly important goal for the ocean. Our work builds a skillful global emulator of the ocean component of a state-of-the-art climate model. We emulate key ocean variables, sea surface height, horizontal velocities, temperature, and salinity, across their full depth. We use a modified ConvNeXt UNet architecture trained on multidepth levels of ocean data. We show that the ocean emulator - Samudra - which exhibits no drift relative to the truth, can reproduce the depth structure of ocean variables and their interannual variability. Samudra is stable for centuries and 150 times faster than the original ocean model. Samudra struggles to capture the correct magnitude of the forcing trends and simultaneously remains stable, requiring further work.

Explaining the physics of transfer learning a data-driven subgrid-scale closure to a different turbulent flow

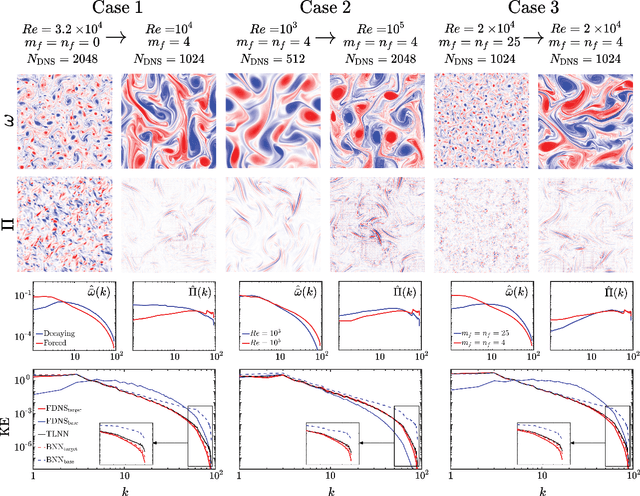
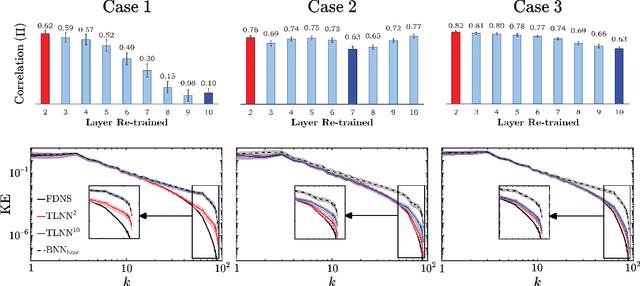
Transfer learning (TL) is becoming a powerful tool in scientific applications of neural networks (NNs), such as weather/climate prediction and turbulence modeling. TL enables out-of-distribution generalization (e.g., extrapolation in parameters) and effective blending of disparate training sets (e.g., simulations and observations). In TL, selected layers of a NN, already trained for a base system, are re-trained using a small dataset from a target system. For effective TL, we need to know 1) what are the best layers to re-train? and 2) what physics are learned during TL? Here, we present novel analyses and a new framework to address (1)-(2) for a broad range of multi-scale, nonlinear systems. Our approach combines spectral analyses of the systems' data with spectral analyses of convolutional NN's activations and kernels, explaining the inner-workings of TL in terms of the system's nonlinear physics. Using subgrid-scale modeling of several setups of 2D turbulence as test cases, we show that the learned kernels are combinations of low-, band-, and high-pass filters, and that TL learns new filters whose nature is consistent with the spectral differences of base and target systems. We also find the shallowest layers are the best to re-train in these cases, which is against the common wisdom guiding TL in machine learning literature. Our framework identifies the best layer(s) to re-train beforehand, based on physics and NN theory. Together, these analyses explain the physics learned in TL and provide a framework to guide TL for wide-ranging applications in science and engineering, such as climate change modeling.

Data-driven super-parameterization using deep learning: Experimentation with multi-scale Lorenz 96 systems and transfer-learning

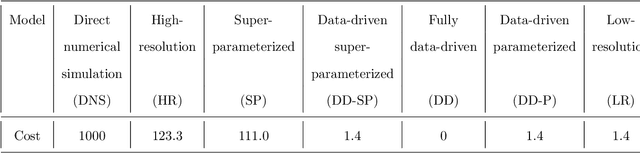
To make weather/climate modeling computationally affordable, small-scale processes are usually represented in terms of the large-scale, explicitly-resolved processes using physics-based or semi-empirical parameterization schemes. Another approach, computationally more demanding but often more accurate, is super-parameterization (SP), which involves integrating the equations of small-scale processes on high-resolution grids embedded within the low-resolution grids of large-scale processes. Recently, studies have used machine learning (ML) to develop data-driven parameterization (DD-P) schemes. Here, we propose a new approach, data-driven SP (DD-SP), in which the equations of the small-scale processes are integrated data-drivenly using ML methods such as recurrent neural networks. Employing multi-scale Lorenz 96 systems as testbed, we compare the cost and accuracy (in terms of both short-term prediction and long-term statistics) of parameterized low-resolution (LR), SP, DD-P, and DD-SP models. We show that with the same computational cost, DD-SP substantially outperforms LR, and is better than DD-P, particularly when scale separation is lacking. DD-SP is much cheaper than SP, yet its accuracy is the same in reproducing long-term statistics and often comparable in short-term forecasting. We also investigate generalization, finding that when models trained on data from one system are applied to a system with different forcing (e.g., more chaotic), the models often do not generalize, particularly when the short-term prediction accuracy is examined. But we show that transfer-learning, which involves re-training the data-driven model with a small amount of data from the new system, significantly improves generalization. Potential applications of DD-SP and transfer-learning in climate/weather modeling and the expected challenges are discussed.