Generative Lagrangian data assimilation for ocean dynamics under extreme sparsity

Reconstructing ocean dynamics from observational data is fundamentally limited by the sparse, irregular, and Lagrangian nature of spatial sampling, particularly in subsurface and remote regions. This sparsity poses significant challenges for forecasting key phenomena such as eddy shedding and rogue waves. Traditional data assimilation methods and deep learning models often struggle to recover mesoscale turbulence under such constraints. We leverage a deep learning framework that combines neural operators with denoising diffusion probabilistic models (DDPMs) to reconstruct high-resolution ocean states from extremely sparse Lagrangian observations. By conditioning the generative model on neural operator outputs, the framework accurately captures small-scale, high-wavenumber dynamics even at $99\%$ sparsity (for synthetic data) and $99.9\%$ sparsity (for real satellite observations). We validate our method on benchmark systems, synthetic float observations, and real satellite data, demonstrating robust performance under severe spatial sampling limitations as compared to other deep learning baselines.

Fourier analysis of the physics of transfer learning for data-driven subgrid-scale models of ocean turbulence

Transfer learning (TL) is a powerful tool for enhancing the performance of neural networks (NNs) in applications such as weather and climate prediction and turbulence modeling. TL enables models to generalize to out-of-distribution data with minimal training data from the new system. In this study, we employ a 9-layer convolutional NN to predict the subgrid forcing in a two-layer ocean quasi-geostrophic system and examine which metrics best describe its performance and generalizability to unseen dynamical regimes. Fourier analysis of the NN kernels reveals that they learn low-pass, Gabor, and high-pass filters, regardless of whether the training data are isotropic or anisotropic. By analyzing the activation spectra, we identify why NNs fail to generalize without TL and how TL can overcome these limitations: the learned weights and biases from one dataset underestimate the out-of-distribution sample spectra as they pass through the network, leading to an underestimation of output spectra. By re-training only one layer with data from the target system, this underestimation is corrected, enabling the NN to produce predictions that match the target spectra. These findings are broadly applicable to data-driven parameterization of dynamical systems.

Simultaneous emulation and downscaling with physically-consistent deep learning-based regional ocean emulators

Building on top of the success in AI-based atmospheric emulation, we propose an AI-based ocean emulation and downscaling framework focusing on the high-resolution regional ocean over Gulf of Mexico. Regional ocean emulation presents unique challenges owing to the complex bathymetry and lateral boundary conditions as well as from fundamental biases in deep learning-based frameworks, such as instability and hallucinations. In this paper, we develop a deep learning-based framework to autoregressively integrate ocean-surface variables over the Gulf of Mexico at $8$ Km spatial resolution without unphysical drifts over decadal time scales and simulataneously downscale and bias-correct it to $4$ Km resolution using a physics-constrained generative model. The framework shows both short-term skills as well as accurate long-term statistics in terms of mean and variability.

Partition of Unity Physics-Informed Neural Networks (POU-PINNs): An Unsupervised Framework for Physics-Informed Domain Decomposition and Mixtures of Experts

Physics-informed neural networks (PINNs) commonly address ill-posed inverse problems by uncovering unknown physics. This study presents a novel unsupervised learning framework that identifies spatial subdomains with specific governing physics. It uses the partition of unity networks (POUs) to divide the space into subdomains, assigning unique nonlinear model parameters to each, which are integrated into the physics model. A vital feature of this method is a physics residual-based loss function that detects variations in physical properties without requiring labeled data. This approach enables the discovery of spatial decompositions and nonlinear parameters in partial differential equations (PDEs), optimizing the solution space by dividing it into subdomains and improving accuracy. Its effectiveness is demonstrated through applications in porous media thermal ablation and ice-sheet modeling, showcasing its potential for tackling real-world physics challenges.

What You See is Not What You Get: Neural Partial Differential Equations and The Illusion of Learning

Differentiable Programming for scientific machine learning (SciML) has recently seen considerable interest and success, as it directly embeds neural networks inside PDEs, often called as NeuralPDEs, derived from first principle physics. Therefore, there is a widespread assumption in the community that NeuralPDEs are more trustworthy and generalizable than black box models. However, like any SciML model, differentiable programming relies predominantly on high-quality PDE simulations as "ground truth" for training. However, mathematics dictates that these are only discrete numerical approximations of the true physics. Therefore, we ask: Are NeuralPDEs and differentiable programming models trained on PDE simulations as physically interpretable as we think? In this work, we rigorously attempt to answer these questions, using established ideas from numerical analysis, experiments, and analysis of model Jacobians. Our study shows that NeuralPDEs learn the artifacts in the simulation training data arising from the discretized Taylor Series truncation error of the spatial derivatives. Additionally, NeuralPDE models are systematically biased, and their generalization capability is likely enabled by a fortuitous interplay of numerical dissipation and truncation error in the training dataset and NeuralPDE, which seldom happens in practical applications. This bias manifests aggressively even in relatively accessible 1-D equations, raising concerns about the veracity of differentiable programming on complex, high-dimensional, real-world PDEs, and in dataset integrity of foundation models. Further, we observe that the initial condition constrains the truncation error in initial-value problems in PDEs, thereby exerting limitations to extrapolation. Finally, we demonstrate that an eigenanalysis of model weights can indicate a priori if the model will be inaccurate for out-of-distribution testing.

Can AI weather models predict out-of-distribution gray swan tropical cyclones?

Predicting gray swan weather extremes, which are possible but so rare that they are absent from the training dataset, is a major concern for AI weather/climate models. An important open question is whether AI models can extrapolate from weaker weather events present in the training set to stronger, unseen weather extremes. To test this, we train independent versions of the AI model FourCastNet on the 1979-2015 ERA5 dataset with all data, or with Category 3-5 tropical cyclones (TCs) removed, either globally or only over the North Atlantic or Western Pacific basin. We then test these versions of FourCastNet on 2018-2023 Category 5 TCs (gray swans). All versions yield similar accuracy for global weather, but the one trained without Category 3-5 TCs cannot accurately forecast Category 5 TCs, indicating that these models cannot extrapolate from weaker storms. The versions trained without Category 3-5 TCs in one basin show some skill forecasting Category 5 TCs in that basin, suggesting that FourCastNet can generalize across tropical basins. This is encouraging and surprising because regional information is implicitly encoded in inputs. No version satisfies gradient-wind balance, implying that enforcing such physical constraints may not improve generalizability to gray swans. Given that current state-of-the-art AI weather/climate models have similar learning strategies, we expect our findings to apply to other models and extreme events. Our work demonstrates that novel learning strategies are needed for AI weather/climate models to provide early warning or estimated statistics for the rarest, most impactful weather extremes.

Improved deep learning of chaotic dynamical systems with multistep penalty losses

Predicting the long-term behavior of chaotic systems remains a formidable challenge due to their extreme sensitivity to initial conditions and the inherent limitations of traditional data-driven modeling approaches. This paper introduces a novel framework that addresses these challenges by leveraging the recently proposed multi-step penalty (MP) optimization technique. Our approach extends the applicability of MP optimization to a wide range of deep learning architectures, including Fourier Neural Operators and UNETs. By introducing penalized local discontinuities in the forecast trajectory, we effectively handle the non-convexity of loss landscapes commonly encountered in training neural networks for chaotic systems. We demonstrate the effectiveness of our method through its application to two challenging use-cases: the prediction of flow velocity evolution in two-dimensional turbulence and ocean dynamics using reanalysis data. Our results highlight the potential of this approach for accurate and stable long-term prediction of chaotic dynamics, paving the way for new advancements in data-driven modeling of complex natural phenomena.

LUCIE: A Lightweight Uncoupled ClImate Emulator with long-term stability and physical consistency for O(1000)-member ensembles

We present LUCIE, a $1000$- member ensemble data-driven atmospheric emulator that remains stable during autoregressive inference for thousands of years without a drifting climatology. LUCIE has been trained on $9.5$ years of coarse-resolution ERA5 data with $4$ prognostic variables on a single A100 GPU for $2.4$ h. Owing to the cheap computational cost of inference, $1000$ model ensembles are executed for $5$ years to compute an uncertainty-quantified climatology for the prognostic variables that closely match the climatology obtained from ERA5. Unlike all the other state-of-the-art AI weather models, LUCIE is neither unstable nor does it produce hallucinations that result in unphysical drift of the emulated climate. Furthermore, LUCIE \textbf{does not impose} ``true" sea-surface temperature (SST) from a coupled numerical model to enforce the annual cycle in temperature. We demonstrate the long-term climatology obtained from LUCIE as well as subseasonal-to-seasonal scale prediction skills on the prognostic variables. We also demonstrate a $20$-year emulation with LUCIE here: https://drive.google.com/file/d/1mRmhx9RRGiF3uGo_mRQK8RpwQatrCiMn/view

OceanNet: A principled neural operator-based digital twin for regional oceans

While data-driven approaches demonstrate great potential in atmospheric modeling and weather forecasting, ocean modeling poses distinct challenges due to complex bathymetry, land, vertical structure, and flow non-linearity. This study introduces OceanNet, a principled neural operator-based digital twin for ocean circulation. OceanNet uses a Fourier neural operator and predictor-evaluate-corrector integration scheme to mitigate autoregressive error growth and enhance stability over extended time scales. A spectral regularizer counteracts spectral bias at smaller scales. OceanNet is applied to the northwest Atlantic Ocean western boundary current (the Gulf Stream), focusing on the task of seasonal prediction for Loop Current eddies and the Gulf Stream meander. Trained using historical sea surface height (SSH) data, OceanNet demonstrates competitive forecast skill by outperforming SSH predictions by an uncoupled, state-of-the-art dynamical ocean model forecast, reducing computation by 500,000 times. These accomplishments demonstrate the potential of physics-inspired deep neural operators as cost-effective alternatives to high-resolution numerical ocean models.

Learning Closed-form Equations for Subgrid-scale Closures from High-fidelity Data: Promises and Challenges

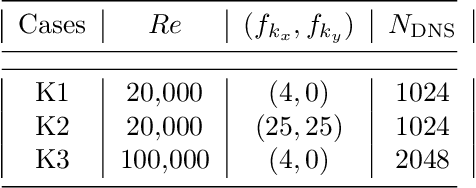
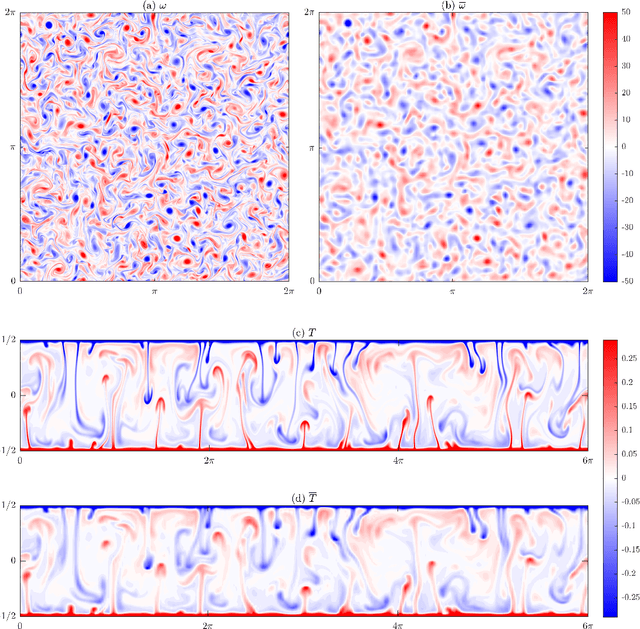
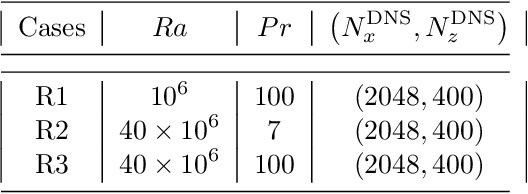
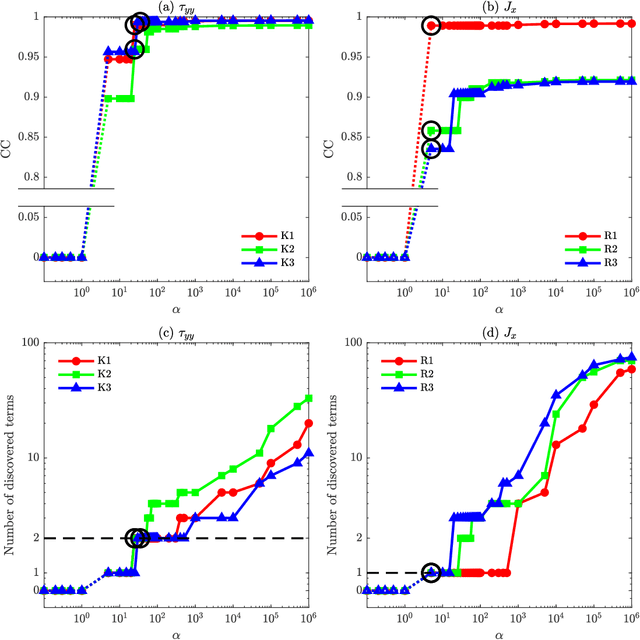
There is growing interest in discovering interpretable, closed-form equations for subgrid-scale (SGS) closures/parameterizations of complex processes in Earth system. Here, we apply a common equation-discovery technique with expansive libraries to learn closures from filtered direct numerical simulations of 2D forced turbulence and Rayleigh-B\'enard convection (RBC). Across common filters, we robustly discover closures of the same form for momentum and heat fluxes. These closures depend on nonlinear combinations of gradients of filtered variables (velocity, temperature), with constants that are independent of the fluid/flow properties and only depend on filter type/size. We show that these closures are the nonlinear gradient model (NGM), which is derivable analytically using Taylor-series expansions. In fact, we suggest that with common (physics-free) equation-discovery algorithms, regardless of the system/physics, discovered closures are always consistent with the Taylor-series. Like previous studies, we find that large-eddy simulations with NGM closures are unstable, despite significant similarities between the true and NGM-predicted fluxes (pattern correlations $> 0.95$). We identify two shortcomings as reasons for these instabilities: in 2D, NGM produces zero kinetic energy transfer between resolved and subgrid scales, lacking both diffusion and backscattering. In RBC, backscattering of potential energy is poorly predicted. Moreover, we show that SGS fluxes diagnosed from data, presumed the "truth" for discovery, depend on filtering procedures and are not unique. Accordingly, to learn accurate, stable closures from high-fidelity data in future work, we propose several ideas around using physics-informed libraries, loss functions, and metrics. These findings are relevant beyond turbulence to closure modeling of any multi-scale system.