Learning Closed-form Equations for Subgrid-scale Closures from High-fidelity Data: Promises and Challenges

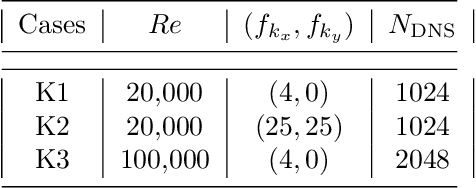
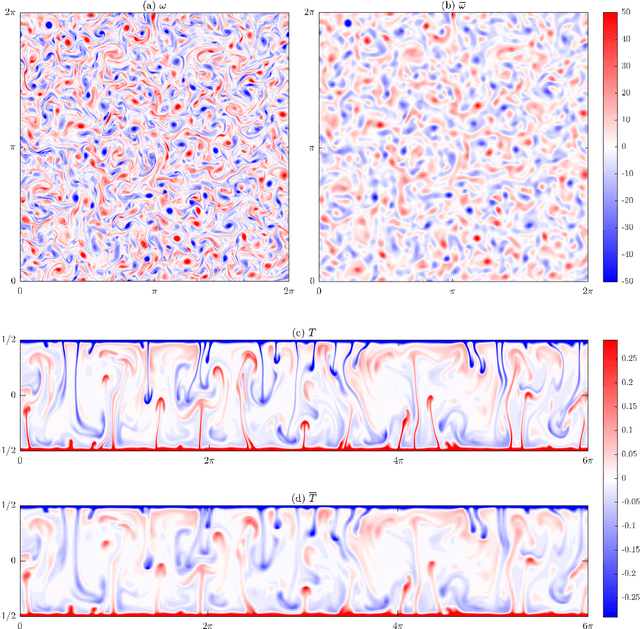
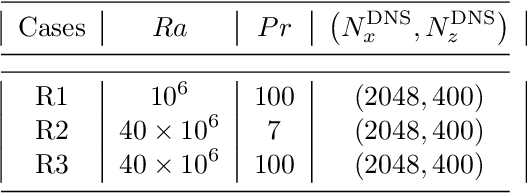
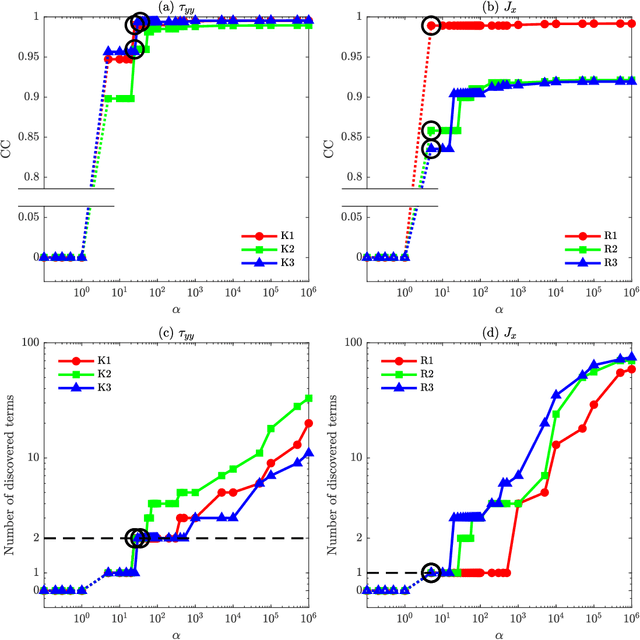
There is growing interest in discovering interpretable, closed-form equations for subgrid-scale (SGS) closures/parameterizations of complex processes in Earth system. Here, we apply a common equation-discovery technique with expansive libraries to learn closures from filtered direct numerical simulations of 2D forced turbulence and Rayleigh-B\'enard convection (RBC). Across common filters, we robustly discover closures of the same form for momentum and heat fluxes. These closures depend on nonlinear combinations of gradients of filtered variables (velocity, temperature), with constants that are independent of the fluid/flow properties and only depend on filter type/size. We show that these closures are the nonlinear gradient model (NGM), which is derivable analytically using Taylor-series expansions. In fact, we suggest that with common (physics-free) equation-discovery algorithms, regardless of the system/physics, discovered closures are always consistent with the Taylor-series. Like previous studies, we find that large-eddy simulations with NGM closures are unstable, despite significant similarities between the true and NGM-predicted fluxes (pattern correlations $> 0.95$). We identify two shortcomings as reasons for these instabilities: in 2D, NGM produces zero kinetic energy transfer between resolved and subgrid scales, lacking both diffusion and backscattering. In RBC, backscattering of potential energy is poorly predicted. Moreover, we show that SGS fluxes diagnosed from data, presumed the "truth" for discovery, depend on filtering procedures and are not unique. Accordingly, to learn accurate, stable closures from high-fidelity data in future work, we propose several ideas around using physics-informed libraries, loss functions, and metrics. These findings are relevant beyond turbulence to closure modeling of any multi-scale system.