Extreme Event Prediction with Multi-agent Reinforcement Learning-based Parametrization of Atmospheric and Oceanic Turbulence

Global climate models (GCMs) are the main tools for understanding and predicting climate change. However, due to limited numerical resolutions, these models suffer from major structural uncertainties; e.g., they cannot resolve critical processes such as small-scale eddies in atmospheric and oceanic turbulence. Thus, such small-scale processes have to be represented as a function of the resolved scales via closures (parametrization). The accuracy of these closures is particularly important for capturing climate extremes. Traditionally, such closures are based on heuristics and simplifying assumptions about the unresolved physics. Recently, supervised-learned closures, trained offline on high-fidelity data, have been shown to outperform the classical physics-based closures. However, this approach requires a significant amount of high-fidelity training data and can also lead to instabilities. Reinforcement learning is emerging as a potent alternative for developing such closures as it requires only low-order statistics and leads to stable closures. In Scientific Multi-Agent Reinforcement Learning (SMARL) computational elements serve a dual role of discretization points and learning agents. We leverage SMARL and fundamentals of turbulence physics to learn closures for prototypes of atmospheric and oceanic turbulence. The policy is trained using only the enstrophy spectrum, which is nearly invariant and can be estimated from a few high-fidelity samples (these few samples are far from enough for supervised/offline learning). We show that these closures lead to stable low-resolution simulations that, at a fraction of the cost, can reproduce the high-fidelity simulations' statistics, including the tails of the probability density functions. The results demonstrate the high potential of SMARL for closure modeling for GCMs, especially in the regime of scarce data and indirect observations.

Learning Closed-form Equations for Subgrid-scale Closures from High-fidelity Data: Promises and Challenges

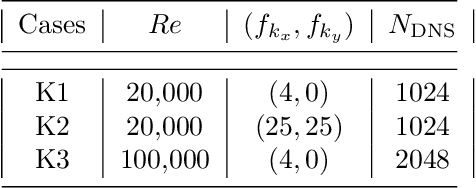
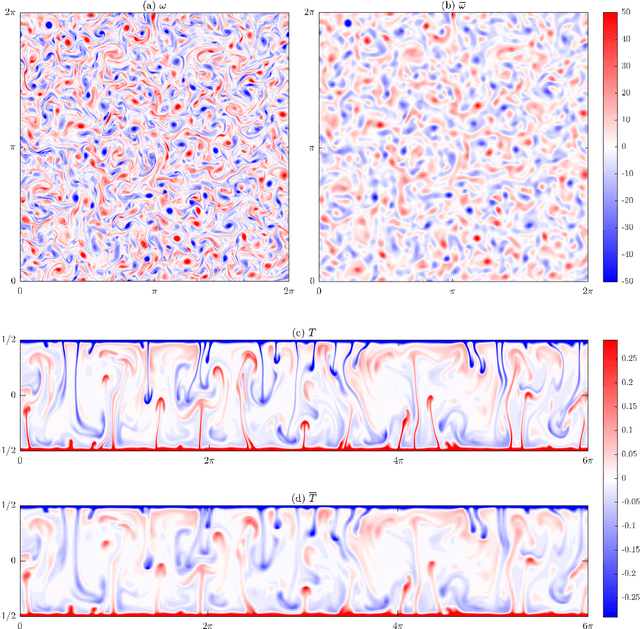
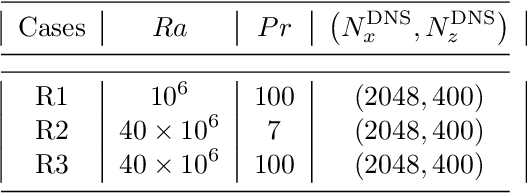
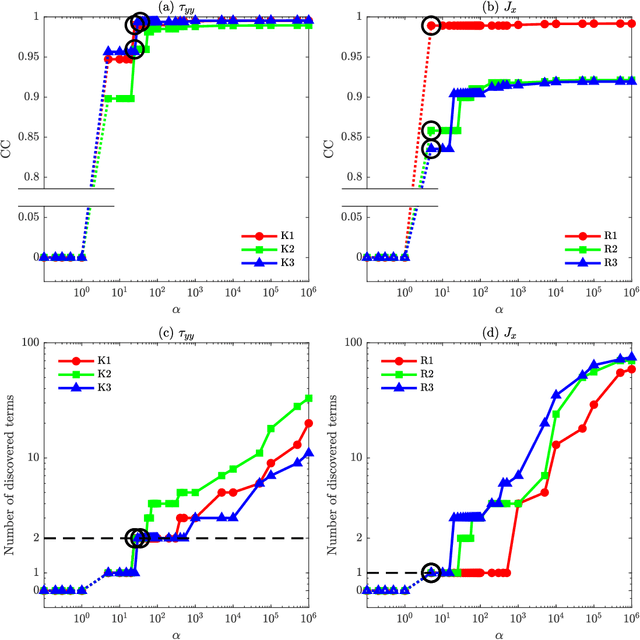
There is growing interest in discovering interpretable, closed-form equations for subgrid-scale (SGS) closures/parameterizations of complex processes in Earth system. Here, we apply a common equation-discovery technique with expansive libraries to learn closures from filtered direct numerical simulations of 2D forced turbulence and Rayleigh-B\'enard convection (RBC). Across common filters, we robustly discover closures of the same form for momentum and heat fluxes. These closures depend on nonlinear combinations of gradients of filtered variables (velocity, temperature), with constants that are independent of the fluid/flow properties and only depend on filter type/size. We show that these closures are the nonlinear gradient model (NGM), which is derivable analytically using Taylor-series expansions. In fact, we suggest that with common (physics-free) equation-discovery algorithms, regardless of the system/physics, discovered closures are always consistent with the Taylor-series. Like previous studies, we find that large-eddy simulations with NGM closures are unstable, despite significant similarities between the true and NGM-predicted fluxes (pattern correlations $> 0.95$). We identify two shortcomings as reasons for these instabilities: in 2D, NGM produces zero kinetic energy transfer between resolved and subgrid scales, lacking both diffusion and backscattering. In RBC, backscattering of potential energy is poorly predicted. Moreover, we show that SGS fluxes diagnosed from data, presumed the "truth" for discovery, depend on filtering procedures and are not unique. Accordingly, to learn accurate, stable closures from high-fidelity data in future work, we propose several ideas around using physics-informed libraries, loss functions, and metrics. These findings are relevant beyond turbulence to closure modeling of any multi-scale system.

Explaining the physics of transfer learning a data-driven subgrid-scale closure to a different turbulent flow

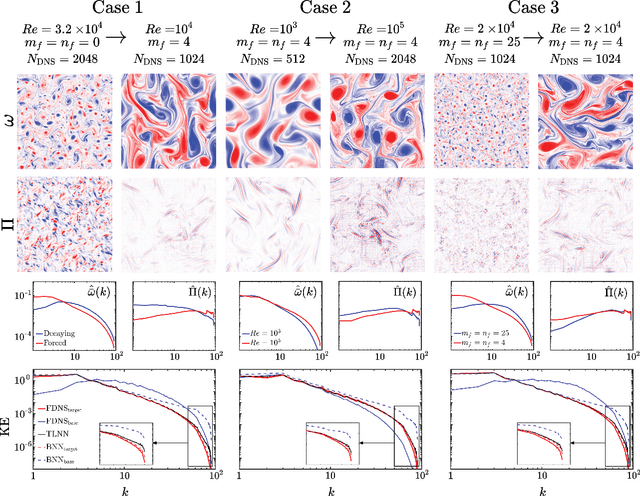
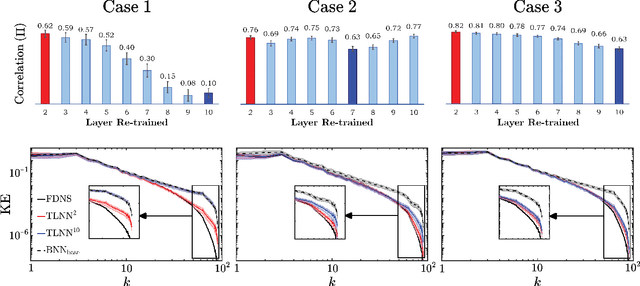
Transfer learning (TL) is becoming a powerful tool in scientific applications of neural networks (NNs), such as weather/climate prediction and turbulence modeling. TL enables out-of-distribution generalization (e.g., extrapolation in parameters) and effective blending of disparate training sets (e.g., simulations and observations). In TL, selected layers of a NN, already trained for a base system, are re-trained using a small dataset from a target system. For effective TL, we need to know 1) what are the best layers to re-train? and 2) what physics are learned during TL? Here, we present novel analyses and a new framework to address (1)-(2) for a broad range of multi-scale, nonlinear systems. Our approach combines spectral analyses of the systems' data with spectral analyses of convolutional NN's activations and kernels, explaining the inner-workings of TL in terms of the system's nonlinear physics. Using subgrid-scale modeling of several setups of 2D turbulence as test cases, we show that the learned kernels are combinations of low-, band-, and high-pass filters, and that TL learns new filters whose nature is consistent with the spectral differences of base and target systems. We also find the shallowest layers are the best to re-train in these cases, which is against the common wisdom guiding TL in machine learning literature. Our framework identifies the best layer(s) to re-train beforehand, based on physics and NN theory. Together, these analyses explain the physics learned in TL and provide a framework to guide TL for wide-ranging applications in science and engineering, such as climate change modeling.