A Critical Assessment of Pattern Comparisons Between POD and Autoencoders in Intraventricular Flows

Understanding intraventricular hemodynamics requires compact and physically interpretable representations of the underlying flow structures, as characteristic flow patterns are closely associated with cardiovascular conditions and can support early detection of cardiac deterioration. Conventional visualization of velocity or pressure fields, however, provides limited insight into the coherent mechanisms driving these dynamics. Reduced-order modeling techniques, like Proper Orthogonal Decomposition (POD) and Autoencoder (AE) architectures, offer powerful alternatives to extract dominant flow features from complex datasets. This study systematically compares POD with several AE variants (Linear, Nonlinear, Convolutional, and Variational) using left ventricular flow fields obtained from computational fluid dynamics simulations. We show that, for a suitably chosen latent dimension, AEs produce modes that become nearly orthogonal and qualitatively resemble POD modes that capture a given percentage of kinetic energy. As the number of latent modes increases, AE modes progressively lose orthogonality, leading to linear dependence, spatial redundancy, and the appearance of repeated modes with substantial high-frequency content. This degradation reduces interpretability and introduces noise-like components into AE-based reduced-order models, potentially complicating their integration with physics-based formulations or neural-network surrogates. The extent of interpretability loss varies across the AEs, with nonlinear, convolutional, and variational models exhibiting distinct behaviors in orthogonality preservation and feature localization. Overall, the results indicate that AEs can reproduce POD-like coherent structures under specific latent-space configurations, while highlighting the need for careful mode selection to ensure physically meaningful representations of cardiac flow dynamics.

Generative Urban Flow Modeling: From Geometry to Airflow with Graph Diffusion

Urban wind flow modeling and simulation play an important role in air quality assessment and sustainable city planning. A key challenge for modeling and simulation is handling the complex geometries of the urban landscape. Low order models are limited in capturing the effects of geometry, while high-fidelity Computational Fluid Dynamics (CFD) simulations are prohibitively expensive, especially across multiple geometries or wind conditions. Here, we propose a generative diffusion framework for synthesizing steady-state urban wind fields over unstructured meshes that requires only geometry information. The framework combines a hierarchical graph neural network with score-based diffusion modeling to generate accurate and diverse velocity fields without requiring temporal rollouts or dense measurements. Trained across multiple mesh slices and wind angles, the model generalizes to unseen geometries, recovers key flow structures such as wakes and recirculation zones, and offers uncertainty-aware predictions. Ablation studies confirm robustness to mesh variation and performance under different inference regimes. This work develops is the first step towards foundation models for the built environment that can help urban planners rapidly evaluate design decisions under densification and climate uncertainty.

Symmetry aware Reynolds Averaged Navier Stokes turbulence models with equivariant neural networks

Accurate and generalizable Reynolds-averaged Navier-Stokes (RANS) models for turbulent flows rely on effective closures. We introduce tensor-based, symmetry aware closures using equivariant neural networks (ENNs) and present an algorithm for enforcing algebraic contraction relations among tensor components. The modeling approach builds on the structure tensor framework introduced by Kassinos and Reynolds to learn closures in the rapid distortion theory setting. Experiments show that ENNs can effectively learn relationships involving high-order tensors, meeting or exceeding the performance of existing models in tasks such as predicting the rapid pressure-strain correlation. Our results show that ENNs provide a physically consistent alternative to classical tensor basis models, enabling end-to-end learning of unclosed terms in RANS and fast exploration of model dependencies.

Reinforcement Learning Closures for Underresolved Partial Differential Equations using Synthetic Data

Partial Differential Equations (PDEs) describe phenomena ranging from turbulence and epidemics to quantum mechanics and financial markets. Despite recent advances in computational science, solving such PDEs for real-world applications remains prohibitively expensive because of the necessity of resolving a broad range of spatiotemporal scales. In turn, practitioners often rely on coarse-grained approximations of the original PDEs, trading off accuracy for reduced computational resources. To mitigate the loss of detail inherent in such approximations, closure models are employed to represent unresolved spatiotemporal interactions. We present a framework for developing closure models for PDEs using synthetic data acquired through the method of manufactured solutions. These data are used in conjunction with reinforcement learning to provide closures for coarse-grained PDEs. We illustrate the efficacy of our method using the one-dimensional and two-dimensional Burgers' equations and the two-dimensional advection equation. Moreover, we demonstrate that closure models trained for inhomogeneous PDEs can be effectively generalized to homogeneous PDEs. The results demonstrate the potential for developing accurate and computationally efficient closure models for systems with scarce data.

Optimal Lattice Boltzmann Closures through Multi-Agent Reinforcement Learning

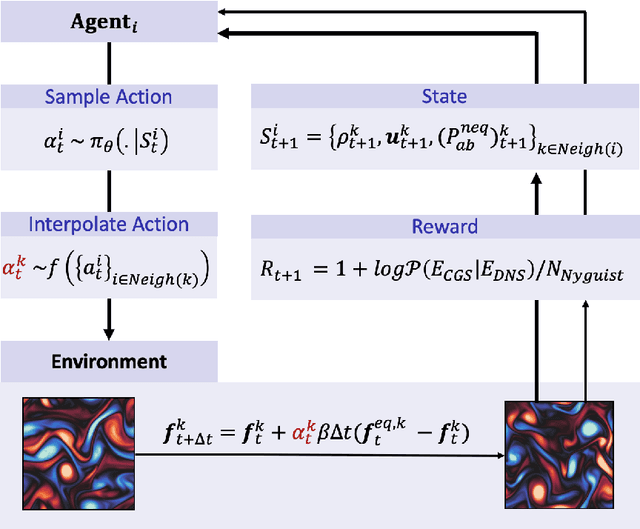
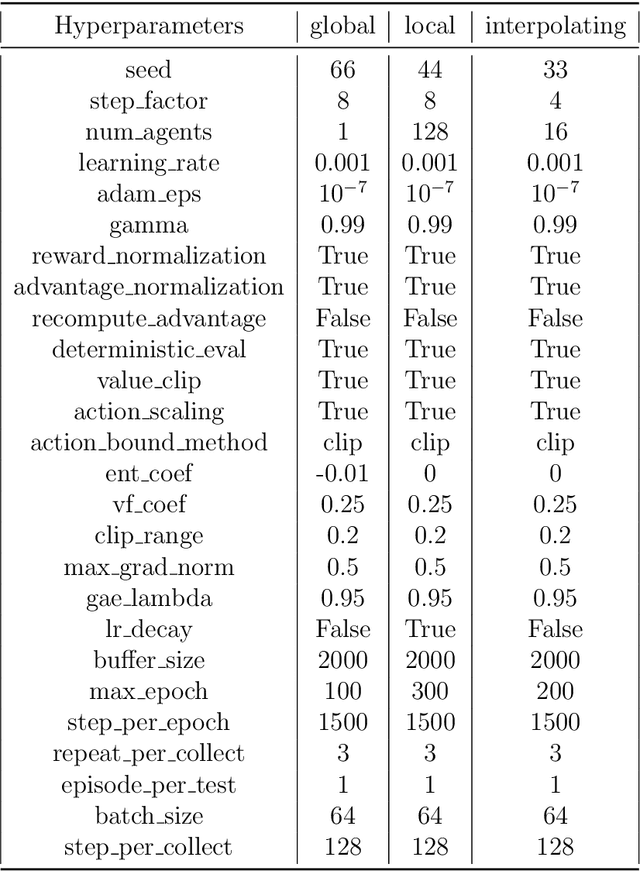
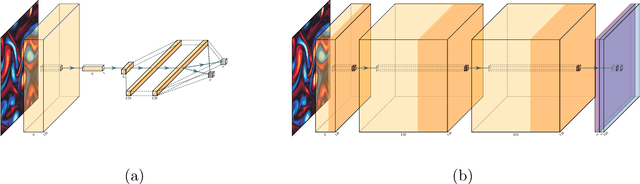
The Lattice Boltzmann method (LBM) offers a powerful and versatile approach to simulating diverse hydrodynamic phenomena, spanning microfluidics to aerodynamics. The vast range of spatiotemporal scales inherent in these systems currently renders full resolution impractical, necessitating the development of effective closure models for under-resolved simulations. Under-resolved LBMs are unstable, and while there is a number of important efforts to stabilize them, they often face limitations in generalizing across scales and physical systems. We present a novel, data-driven, multiagent reinforcement learning (MARL) approach that drastically improves stability and accuracy of coarse-grained LBM simulations. The proposed method uses a convolutional neural network to dynamically control the local relaxation parameter for the LB across the simulation grid. The LB-MARL framework is showcased in turbulent Kolmogorov flows. We find that the MARL closures stabilize the simulations and recover the energy spectra of significantly more expensive fully resolved simulations while maintaining computational efficiency. The learned closure model can be transferred to flow scenarios unseen during training and has improved robustness and spectral accuracy compared to traditional LBM models. We believe that MARL closures open new frontiers for efficient and accurate simulations of a multitude of complex problems not accessible to present-day LB methods alone.

Energy Matching: Unifying Flow Matching and Energy-Based Models for Generative Modeling

Generative models often map noise to data by matching flows or scores, but these approaches become cumbersome for incorporating partial observations or additional priors. Inspired by recent advances in Wasserstein gradient flows, we propose Energy Matching, a framework that unifies flow-based approaches with the flexibility of energy-based models (EBMs). Far from the data manifold, samples move along curl-free, optimal transport paths from noise to data. As they approach the data manifold, an entropic energy term guides the system into a Boltzmann equilibrium distribution, explicitly capturing the underlying likelihood structure of the data. We parameterize this dynamic with a single time-independent scalar field, which serves as both a powerful generator and a flexible prior for effective regularization of inverse problems. Our method substantially outperforms existing EBMs on CIFAR-10 generation (FID 3.97 compared to 8.61), while retaining the simulation-free training of transport-based approaches away from the data manifold. Additionally, we exploit the flexibility of our method and introduce an interaction energy for diverse mode exploration. Our approach focuses on learning a static scalar potential energy -- without time conditioning, auxiliary generators, or additional networks -- marking a significant departure from recent EBM methods. We believe this simplified framework significantly advances EBM capabilities and paves the way for their broader adoption in generative modeling across diverse domains.

Learning Effective Dynamics across Spatio-Temporal Scales of Complex Flows

Modeling and simulation of complex fluid flows with dynamics that span multiple spatio-temporal scales is a fundamental challenge in many scientific and engineering domains. Full-scale resolving simulations for systems such as highly turbulent flows are not feasible in the foreseeable future, and reduced-order models must capture dynamics that involve interactions across scales. In the present work, we propose a novel framework, Graph-based Learning of Effective Dynamics (Graph-LED), that leverages graph neural networks (GNNs), as well as an attention-based autoregressive model, to extract the effective dynamics from a small amount of simulation data. GNNs represent flow fields on unstructured meshes as graphs and effectively handle complex geometries and non-uniform grids. The proposed method combines a GNN based, dimensionality reduction for variable-size unstructured meshes with an autoregressive temporal attention model that can learn temporal dependencies automatically. We evaluated the proposed approach on a suite of fluid dynamics problems, including flow past a cylinder and flow over a backward-facing step over a range of Reynolds numbers. The results demonstrate robust and effective forecasting of spatio-temporal physics; in the case of the flow past a cylinder, both small-scale effects that occur close to the cylinder as well as its wake are accurately captured.

Deconstructing Recurrence, Attention, and Gating: Investigating the transferability of Transformers and Gated Recurrent Neural Networks in forecasting of dynamical systems

Machine learning architectures, including transformers and recurrent neural networks (RNNs) have revolutionized forecasting in applications ranging from text processing to extreme weather. Notably, advanced network architectures, tuned for applications such as natural language processing, are transferable to other tasks such as spatiotemporal forecasting tasks. However, there is a scarcity of ablation studies to illustrate the key components that enable this forecasting accuracy. The absence of such studies, although explainable due to the associated computational cost, intensifies the belief that these models ought to be considered as black boxes. In this work, we decompose the key architectural components of the most powerful neural architectures, namely gating and recurrence in RNNs, and attention mechanisms in transformers. Then, we synthesize and build novel hybrid architectures from the standard blocks, performing ablation studies to identify which mechanisms are effective for each task. The importance of considering these components as hyper-parameters that can augment the standard architectures is exhibited on various forecasting datasets, from the spatiotemporal chaotic dynamics of the multiscale Lorenz 96 system, the Kuramoto-Sivashinsky equation, as well as standard real world time-series benchmarks. A key finding is that neural gating and attention improves the performance of all standard RNNs in most tasks, while the addition of a notion of recurrence in transformers is detrimental. Furthermore, our study reveals that a novel, sparsely used, architecture which integrates Recurrent Highway Networks with neural gating and attention mechanisms, emerges as the best performing architecture in high-dimensional spatiotemporal forecasting of dynamical systems.

Physics-Regularized Multi-Modal Image Assimilation for Brain Tumor Localization

Physical models in the form of partial differential equations represent an important prior for many under-constrained problems. One example is tumor treatment planning, which heavily depends on accurate estimates of the spatial distribution of tumor cells in a patient's anatomy. Medical imaging scans can identify the bulk of the tumor, but they cannot reveal its full spatial distribution. Tumor cells at low concentrations remain undetectable, for example, in the most frequent type of primary brain tumors, glioblastoma. Deep-learning-based approaches fail to estimate the complete tumor cell distribution due to a lack of reliable training data. Most existing works therefore rely on physics-based simulations to match observed tumors, providing anatomically and physiologically plausible estimations. However, these approaches struggle with complex and unknown initial conditions and are limited by overly rigid physical models. In this work, we present a novel method that balances data-driven and physics-based cost functions. In particular, we propose a unique discretization scheme that quantifies the adherence of our learned spatiotemporal tumor and brain tissue distributions to their corresponding growth and elasticity equations. This quantification, serving as a regularization term rather than a hard constraint, enables greater flexibility and proficiency in assimilating patient data than existing models. We demonstrate improved coverage of tumor recurrence areas compared to existing techniques on real-world data from a cohort of patients. The method holds the potential to enhance clinical adoption of model-driven treatment planning for glioblastoma.

Generative Learning of the Solution of Parametric Partial Differential Equations Using Guided Diffusion Models and Virtual Observations

We introduce a generative learning framework to model high-dimensional parametric systems using gradient guidance and virtual observations. We consider systems described by Partial Differential Equations (PDEs) discretized with structured or unstructured grids. The framework integrates multi-level information to generate high fidelity time sequences of the system dynamics. We demonstrate the effectiveness and versatility of our framework with two case studies in incompressible, two dimensional, low Reynolds cylinder flow on an unstructured mesh and incompressible turbulent channel flow on a structured mesh, both parameterized by the Reynolds number. Our results illustrate the framework's robustness and ability to generate accurate flow sequences across various parameter settings, significantly reducing computational costs allowing for efficient forecasting and reconstruction of flow dynamics.