Andreas Wagner
Physics-Regularized Multi-Modal Image Assimilation for Brain Tumor Localization
Sep 30, 2024



Abstract:Physical models in the form of partial differential equations represent an important prior for many under-constrained problems. One example is tumor treatment planning, which heavily depends on accurate estimates of the spatial distribution of tumor cells in a patient's anatomy. Medical imaging scans can identify the bulk of the tumor, but they cannot reveal its full spatial distribution. Tumor cells at low concentrations remain undetectable, for example, in the most frequent type of primary brain tumors, glioblastoma. Deep-learning-based approaches fail to estimate the complete tumor cell distribution due to a lack of reliable training data. Most existing works therefore rely on physics-based simulations to match observed tumors, providing anatomically and physiologically plausible estimations. However, these approaches struggle with complex and unknown initial conditions and are limited by overly rigid physical models. In this work, we present a novel method that balances data-driven and physics-based cost functions. In particular, we propose a unique discretization scheme that quantifies the adherence of our learned spatiotemporal tumor and brain tissue distributions to their corresponding growth and elasticity equations. This quantification, serving as a regularization term rather than a hard constraint, enables greater flexibility and proficiency in assimilating patient data than existing models. We demonstrate improved coverage of tumor recurrence areas compared to existing techniques on real-world data from a cohort of patients. The method holds the potential to enhance clinical adoption of model-driven treatment planning for glioblastoma.
A matrix math facility for Power ISA processors
Apr 07, 2021



Abstract:Power ISA(TM) Version 3.1 has introduced a new family of matrix math instructions, collectively known as the Matrix-Multiply Assist (MMA) facility. The instructions in this facility implement numerical linear algebra operations on small matrices and are meant to accelerate computation-intensive kernels, such as matrix multiplication, convolution and discrete Fourier transform. These instructions have led to a power- and area-efficient implementation of a high throughput math engine in the future POWER10 processor. Performance per core is 4 times better, at constant frequency, than the previous generation POWER9 processor. We also advocate the use of compiler built-ins as the preferred way of leveraging these instructions, which we illustrate through case studies covering matrix multiplication and convolution.
Machine Learning on EPEX Order Books: Insights and Forecasts
Jun 27, 2019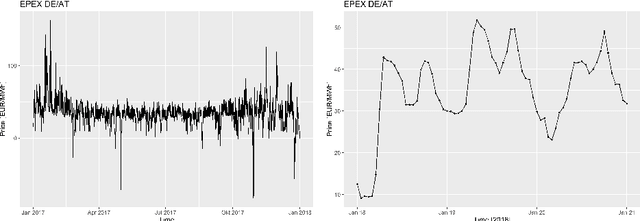
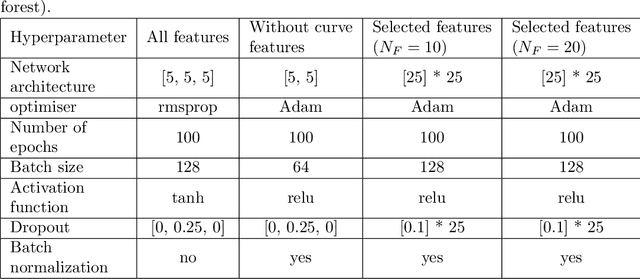
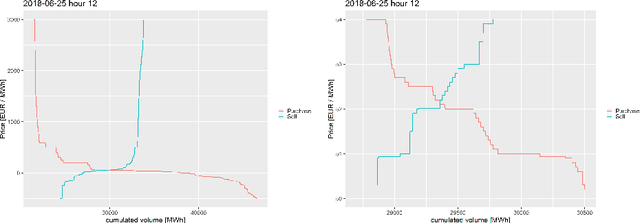
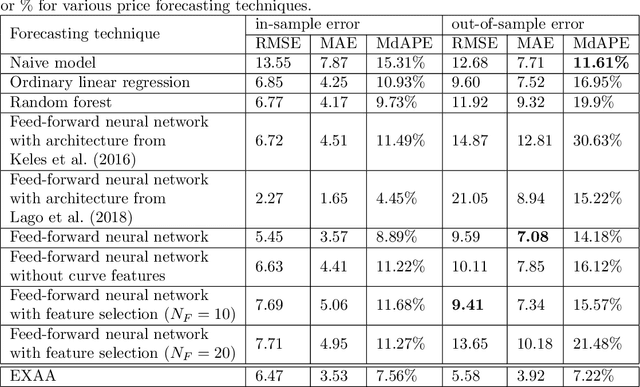
Abstract:This paper employs machine learning algorithms to forecast German electricity spot market prices. The forecasts utilize in particular bid and ask order book data from the spot market but also fundamental market data like renewable infeed and expected demand. Appropriate feature extraction for the order book data is developed. Using cross-validation to optimise hyperparameters, neural networks and random forests are proposed and compared to statistical reference models. The machine learning models outperform traditional approaches.
Incorporating Road Networks into Territory Design
May 05, 2015



Abstract:Given a set of basic areas, the territory design problem asks to create a predefined number of territories, each containing at least one basic area, such that an objective function is optimized. Desired properties of territories often include a reasonable balance, compact form, contiguity and small average journey times which are usually encoded in the objective function or formulated as constraints. We address the territory design problem by developing graph theoretic models that also consider the underlying road network. The derived graph models enable us to tackle the territory design problem by modifying graph partitioning algorithms and mixed integer programming formulations so that the objective of the planning problem is taken into account. We test and compare the algorithms on several real world instances.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge