Efficient Deep Learning-based Forward Solvers for Brain Tumor Growth Models

Glioblastoma, a highly aggressive brain tumor, poses major challenges due to its poor prognosis and high morbidity rates. Partial differential equation-based models offer promising potential to enhance therapeutic outcomes by simulating patient-specific tumor behavior for improved radiotherapy planning. However, model calibration remains a bottleneck due to the high computational demands of optimization methods like Monte Carlo sampling and evolutionary algorithms. To address this, we recently introduced an approach leveraging a neural forward solver with gradient-based optimization to significantly reduce calibration time. This approach requires a highly accurate and fully differentiable forward model. We investigate multiple architectures, including (i) an enhanced TumorSurrogate, (ii) a modified nnU-Net, and (iii) a 3D Vision Transformer (ViT). The optimized TumorSurrogate achieved the best overall results, excelling in both tumor outline matching and voxel-level prediction of tumor cell concentration. It halved the MSE relative to the baseline model and achieved the highest Dice score across all tumor cell concentration thresholds. Our study demonstrates significant enhancement in forward solver performance and outlines important future research directions.

Spatial Brain Tumor Concentration Estimation for Individualized Radiotherapy Planning

Biophysical modeling of brain tumors has emerged as a promising strategy for personalizing radiotherapy planning by estimating the otherwise hidden distribution of tumor cells within the brain. However, many existing state-of-the-art methods are computationally intensive, limiting their widespread translation into clinical practice. In this work, we propose an efficient and direct method that utilizes soft physical constraints to estimate the tumor cell concentration from preoperative MRI of brain tumor patients. Our approach optimizes a 3D tumor concentration field by simultaneously minimizing the difference between the observed MRI and a physically informed loss function. Compared to existing state-of-the-art techniques, our method significantly improves predicting tumor recurrence on two public datasets with a total of 192 patients while maintaining a clinically viable runtime of under one minute - a substantial reduction from the 30 minutes required by the current best approach. Furthermore, we showcase the generalizability of our framework by incorporating additional imaging information and physical constraints, highlighting its potential to translate to various medical diffusion phenomena with imperfect data.

Physics-Regularized Multi-Modal Image Assimilation for Brain Tumor Localization

Physical models in the form of partial differential equations represent an important prior for many under-constrained problems. One example is tumor treatment planning, which heavily depends on accurate estimates of the spatial distribution of tumor cells in a patient's anatomy. Medical imaging scans can identify the bulk of the tumor, but they cannot reveal its full spatial distribution. Tumor cells at low concentrations remain undetectable, for example, in the most frequent type of primary brain tumors, glioblastoma. Deep-learning-based approaches fail to estimate the complete tumor cell distribution due to a lack of reliable training data. Most existing works therefore rely on physics-based simulations to match observed tumors, providing anatomically and physiologically plausible estimations. However, these approaches struggle with complex and unknown initial conditions and are limited by overly rigid physical models. In this work, we present a novel method that balances data-driven and physics-based cost functions. In particular, we propose a unique discretization scheme that quantifies the adherence of our learned spatiotemporal tumor and brain tissue distributions to their corresponding growth and elasticity equations. This quantification, serving as a regularization term rather than a hard constraint, enables greater flexibility and proficiency in assimilating patient data than existing models. We demonstrate improved coverage of tumor recurrence areas compared to existing techniques on real-world data from a cohort of patients. The method holds the potential to enhance clinical adoption of model-driven treatment planning for glioblastoma.

A Learnable Prior Improves Inverse Tumor Growth Modeling

Biophysical modeling, particularly involving partial differential equations (PDEs), offers significant potential for tailoring disease treatment protocols to individual patients. However, the inverse problem-solving aspect of these models presents a substantial challenge, either due to the high computational requirements of model-based approaches or the limited robustness of deep learning (DL) methods. We propose a novel framework that leverages the unique strengths of both approaches in a synergistic manner. Our method incorporates a DL ensemble for initial parameter estimation, facilitating efficient downstream evolutionary sampling initialized with this DL-based prior. We showcase the effectiveness of integrating a rapid deep-learning algorithm with a high-precision evolution strategy in estimating brain tumor cell concentrations from magnetic resonance images. The DL-Prior plays a pivotal role, significantly constraining the effective sampling-parameter space. This reduction results in a fivefold convergence acceleration and a Dice-score of 95%

The Operating System of the Neuromorphic BrainScaleS-1 System

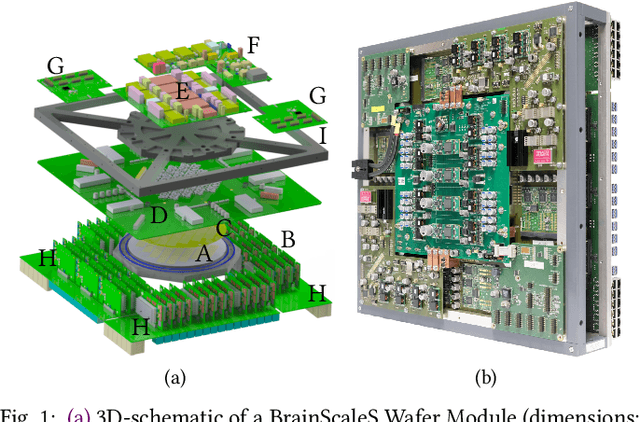
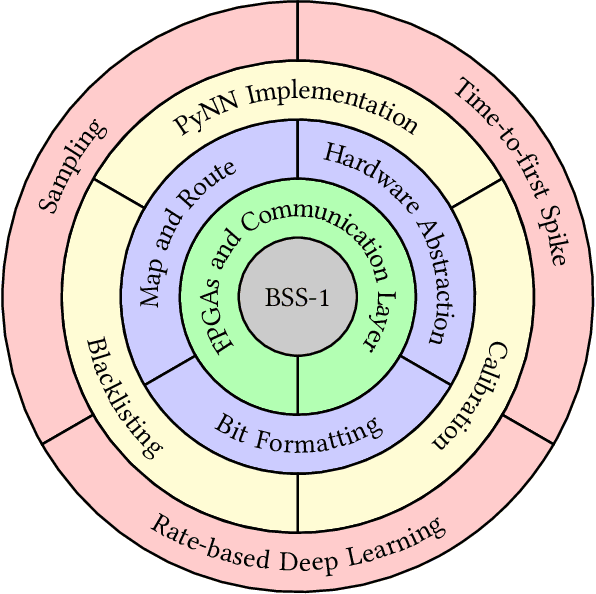
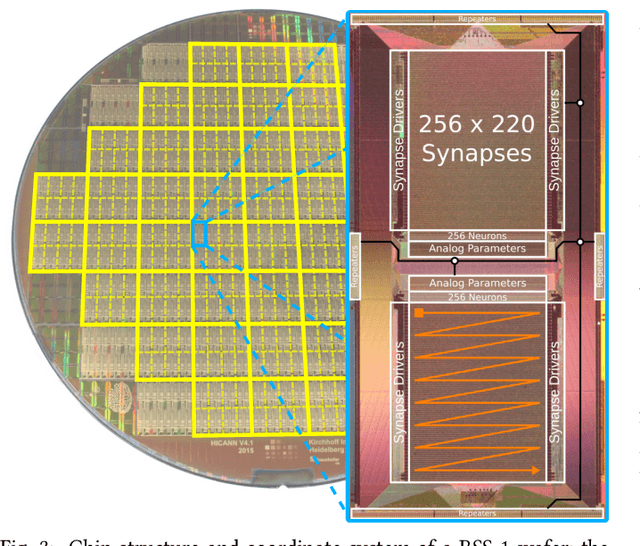
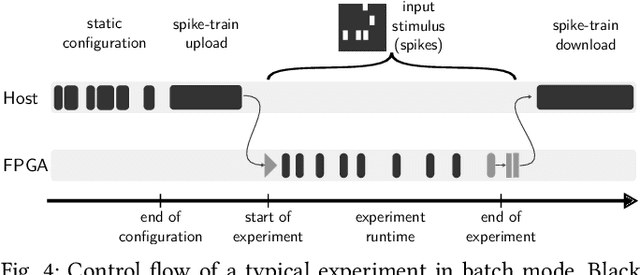
BrainScaleS-1 is a wafer-scale mixed-signal accelerated neuromorphic system targeted for research in the fields of computational neuroscience and beyond-von-Neumann computing. The BrainScaleS Operating System (BrainScaleS OS) is a software stack giving users the possibility to emulate networks described in the high-level network description language PyNN with minimal knowledge of the system. At the same time, expert usage is facilitated by allowing to hook into the system at any depth of the stack. We present operation and development methodologies implemented for the BrainScaleS-1 neuromorphic architecture and walk through the individual components of BrainScaleS OS constituting the software stack for BrainScaleS-1 platform operation.