Pantelis R. Vlachas
Beyond Static Models: Hypernetworks for Adaptive and Generalizable Forecasting in Complex Parametric Dynamical Systems
Jun 24, 2025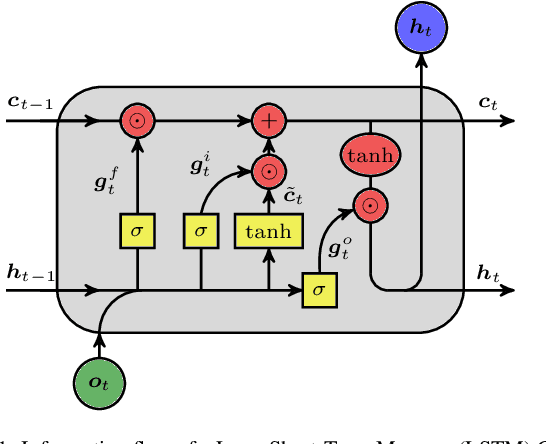

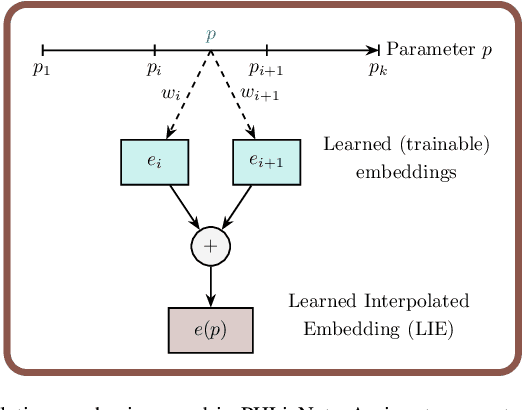
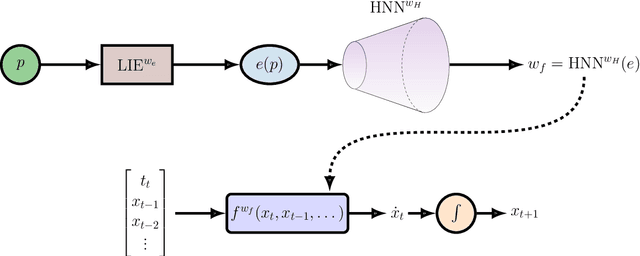
Abstract:Dynamical systems play a key role in modeling, forecasting, and decision-making across a wide range of scientific domains. However, variations in system parameters, also referred to as parametric variability, can lead to drastically different model behavior and output, posing challenges for constructing models that generalize across parameter regimes. In this work, we introduce the Parametric Hypernetwork for Learning Interpolated Networks (PHLieNet), a framework that simultaneously learns: (a) a global mapping from the parameter space to a nonlinear embedding and (b) a mapping from the inferred embedding to the weights of a dynamics propagation network. The learned embedding serves as a latent representation that modulates a base network, termed the hypernetwork, enabling it to generate the weights of a target network responsible for forecasting the system's state evolution conditioned on the previous time history. By interpolating in the space of models rather than observations, PHLieNet facilitates smooth transitions across parameterized system behaviors, enabling a unified model that captures the dynamic behavior across a broad range of system parameterizations. The performance of the proposed technique is validated in a series of dynamical systems with respect to its ability to extrapolate in time and interpolate and extrapolate in the parameter space, i.e., generalize to dynamics that were unseen during training. In all cases, our approach outperforms or matches state-of-the-art baselines in both short-term forecast accuracy and in capturing long-term dynamical features, such as attractor statistics.
Deconstructing Recurrence, Attention, and Gating: Investigating the transferability of Transformers and Gated Recurrent Neural Networks in forecasting of dynamical systems
Oct 03, 2024Abstract:Machine learning architectures, including transformers and recurrent neural networks (RNNs) have revolutionized forecasting in applications ranging from text processing to extreme weather. Notably, advanced network architectures, tuned for applications such as natural language processing, are transferable to other tasks such as spatiotemporal forecasting tasks. However, there is a scarcity of ablation studies to illustrate the key components that enable this forecasting accuracy. The absence of such studies, although explainable due to the associated computational cost, intensifies the belief that these models ought to be considered as black boxes. In this work, we decompose the key architectural components of the most powerful neural architectures, namely gating and recurrence in RNNs, and attention mechanisms in transformers. Then, we synthesize and build novel hybrid architectures from the standard blocks, performing ablation studies to identify which mechanisms are effective for each task. The importance of considering these components as hyper-parameters that can augment the standard architectures is exhibited on various forecasting datasets, from the spatiotemporal chaotic dynamics of the multiscale Lorenz 96 system, the Kuramoto-Sivashinsky equation, as well as standard real world time-series benchmarks. A key finding is that neural gating and attention improves the performance of all standard RNNs in most tasks, while the addition of a notion of recurrence in transformers is detrimental. Furthermore, our study reveals that a novel, sparsely used, architecture which integrates Recurrent Highway Networks with neural gating and attention mechanisms, emerges as the best performing architecture in high-dimensional spatiotemporal forecasting of dynamical systems.
RefreshNet: Learning Multiscale Dynamics through Hierarchical Refreshing
Jan 24, 2024Abstract:Forecasting complex system dynamics, particularly for long-term predictions, is persistently hindered by error accumulation and computational burdens. This study presents RefreshNet, a multiscale framework developed to overcome these challenges, delivering an unprecedented balance between computational efficiency and predictive accuracy. RefreshNet incorporates convolutional autoencoders to identify a reduced order latent space capturing essential features of the dynamics, and strategically employs multiple recurrent neural network (RNN) blocks operating at varying temporal resolutions within the latent space, thus allowing the capture of latent dynamics at multiple temporal scales. The unique "refreshing" mechanism in RefreshNet allows coarser blocks to reset inputs of finer blocks, effectively controlling and alleviating error accumulation. This design demonstrates superiority over existing techniques regarding computational efficiency and predictive accuracy, especially in long-term forecasting. The framework is validated using three benchmark applications: the FitzHugh-Nagumo system, the Reaction-Diffusion equation, and Kuramoto-Sivashinsky dynamics. RefreshNet significantly outperforms state-of-the-art methods in long-term forecasting accuracy and speed, marking a significant advancement in modeling complex systems and opening new avenues in understanding and predicting their behavior.
Adaptive learning of effective dynamics: Adaptive real-time, online modeling for complex systems
Apr 04, 2023Abstract:Predictive simulations are essential for applications ranging from weather forecasting to material design. The veracity of these simulations hinges on their capacity to capture the effective system dynamics. Massively parallel simulations predict the systems dynamics by resolving all spatiotemporal scales, often at a cost that prevents experimentation. On the other hand, reduced order models are fast but often limited by the linearization of the system dynamics and the adopted heuristic closures. We propose a novel systematic framework that bridges large scale simulations and reduced order models to extract and forecast adaptively the effective dynamics (AdaLED) of multiscale systems. AdaLED employs an autoencoder to identify reduced-order representations of the system dynamics and an ensemble of probabilistic recurrent neural networks (RNNs) as the latent time-stepper. The framework alternates between the computational solver and the surrogate, accelerating learned dynamics while leaving yet-to-be-learned dynamics regimes to the original solver. AdaLED continuously adapts the surrogate to the new dynamics through online training. The transitions between the surrogate and the computational solver are determined by monitoring the prediction accuracy and uncertainty of the surrogate. The effectiveness of AdaLED is demonstrated on three different systems - a Van der Pol oscillator, a 2D reaction-diffusion equation, and a 2D Navier-Stokes flow past a cylinder for varying Reynolds numbers (400 up to 1200), showcasing its ability to learn effective dynamics online, detect unseen dynamics regimes, and provide net speed-ups. To the best of our knowledge, AdaLED is the first framework that couples a surrogate model with a computational solver to achieve online adaptive learning of effective dynamics. It constitutes a potent tool for applications requiring many expensive simulations.
Learning from Predictions: Fusing Training and Autoregressive Inference for Long-Term Spatiotemporal Forecasts
Feb 22, 2023Abstract:Recurrent Neural Networks (RNNs) have become an integral part of modeling and forecasting frameworks in areas like natural language processing and high-dimensional dynamical systems such as turbulent fluid flows. To improve the accuracy of predictions, RNNs are trained using the Backpropagation Through Time (BPTT) method to minimize prediction loss. During testing, RNNs are often used in autoregressive scenarios where the output of the network is fed back into the input. However, this can lead to the exposure bias effect, as the network was trained to receive ground-truth data instead of its own predictions. This mismatch between training and testing is compounded when the state distributions are different, and the train and test losses are measured. To address this, previous studies have proposed solutions for language processing networks with probabilistic predictions. Building on these advances, we propose the Scheduled Autoregressive BPTT (BPTT-SA) algorithm for predicting complex systems. Our results show that BPTT-SA effectively reduces iterative error propagation in Convolutional RNNs and Convolutional Autoencoder RNNs, and demonstrate its capabilities in long-term prediction of high-dimensional fluid flows.
Accelerated Simulations of Molecular Systems through Learning of their Effective Dynamics
Feb 17, 2021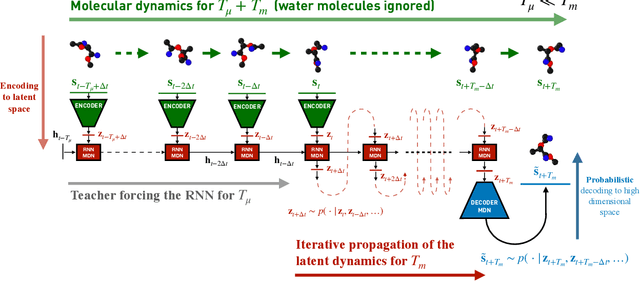
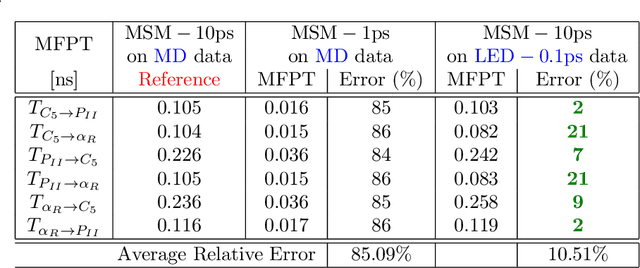
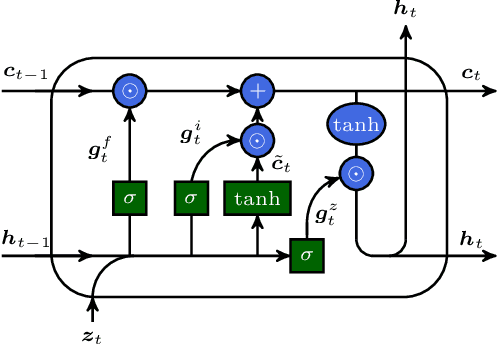
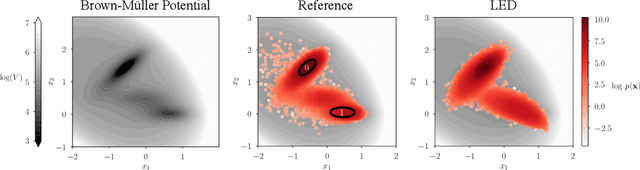
Abstract:Simulations are vital for understanding and predicting the evolution of complex molecular systems. However, despite advances in algorithms and special purpose hardware, accessing the timescales necessary to capture the structural evolution of bio-molecules remains a daunting task. In this work we present a novel framework to advance simulation timescales by up to three orders of magnitude, by learning the effective dynamics (LED) of molecular systems. LED augments the equation-free methodology by employing a probabilistic mapping between coarse and fine scales using mixture density network (MDN) autoencoders and evolves the non-Markovian latent dynamics using long short-term memory MDNs. We demonstrate the effectiveness of LED in the M\"ueller-Brown potential, the Trp Cage protein, and the alanine dipeptide. LED identifies explainable reduced-order representations and can generate, at any instant, the respective all-atom molecular trajectories. We believe that the proposed framework provides a dramatic increase to simulation capabilities and opens new horizons for the effective modeling of complex molecular systems.
Improved Memories Learning
Aug 24, 2020


Abstract:We propose Improved Memories Learning (IMeL), a novel algorithm that turns reinforcement learning (RL) into a supervised learning (SL) problem and delimits the role of neural networks (NN) to interpolation. IMeL consists of two components. The first is a reservoir of experiences. Each experience is updated based on a non-parametric procedural improvement of the policy, computed as a bounded one-sample Monte Carlo estimate. The second is a NN regressor, which receives as input improved experiences from the reservoir (context points) and computes the policy by interpolation. The NN learns to measure the similarity between states in order to compute long-term forecasts by averaging experiences, rather than by encoding the problem structure in the NN parameters. We present preliminary results and propose IMeL as a baseline method for assessing the merits of more complex models and inductive biases.
Learning the Effective Dynamics of Complex Multiscale Systems
Jul 01, 2020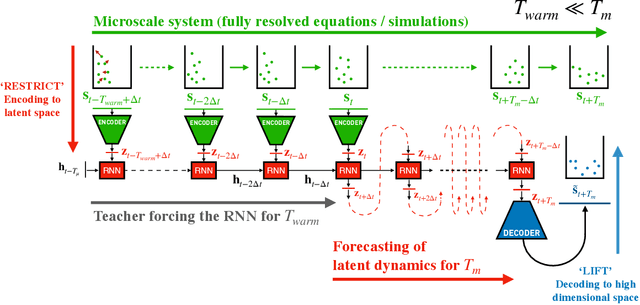


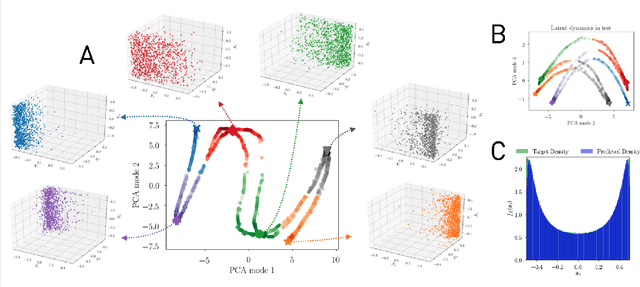
Abstract:Simulations of complex multiscale systems are essential for science and technology ranging from weather forecasting to aircraft design. The predictive capabilities of simulations hinges on their capacity to capture the governing system dynamics. Large scale simulations, resolving all spatiotemporal scales, provide invaluable insight at a high computational cost. In turn, simulations using reduced order models are affordable but their veracity hinges often on linearisation and/or heuristics. Here we present a novel systematic framework to extract and forecast accurately the effective dynamics (LED) of complex systems with multiple spatio-temporal scales. The framework fuses advanced machine learning algorithms with equation-free approaches. It deploys autoencoders to obtain a mapping between fine and coarse grained representations of the system and learns to forecast the latent space dynamics using recurrent neural networks. We compare the LED framework with existing approaches on a number of benchmark problems and demonstrate reduction in computational efforts by several orders of magnitude without sacrificing the accuracy of the system.
Forecasting of Spatio-temporal Chaotic Dynamics with Recurrent Neural Networks: a comparative study of Reservoir Computing and Backpropagation Algorithms
Oct 09, 2019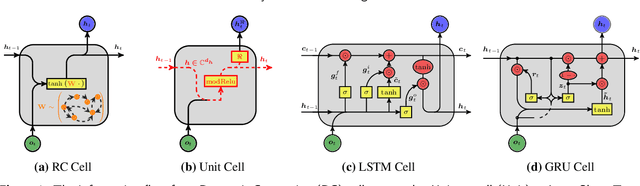
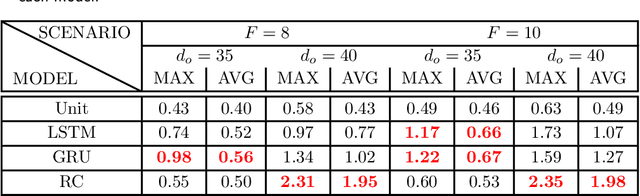
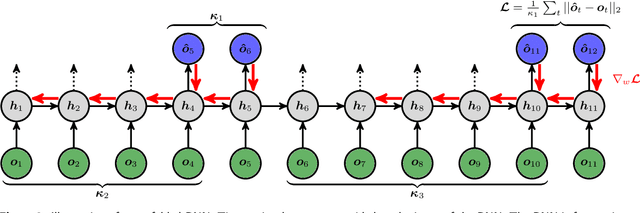
Abstract:How effective are Recurrent Neural Networks (RNNs) in forecasting the spatiotemporal dynamics of chaotic systems ? We address this question through a comparative study of Reservoir Computing (RC) and backpropagation through time (BPTT) algorithms for gated network architectures on a number of benchmark problems. We quantify their relative prediction accuracy on the long-term forecasting of Lorenz-96 and the Kuramoto-Sivashinsky equation and calculation of its Lyapunov spectrum. We discuss their implementation on parallel computers and highlight advantages and limitations of each method. We find that, when the full state dynamics are available for training, RC outperforms BPTT approaches in terms of predictive performance and capturing of the long-term statistics, while at the same time requiring much less time for training. However, in the case of reduced order data, large RC models can be unstable and more likely, than the BPTT algorithms, to diverge in the long term. In contrast, RNNs trained via BPTT capture well the dynamics of these reduced order models. This study confirms that RNNs present a potent computational framework for the forecasting of complex spatio-temporal dynamics.
Data-Driven Forecasting of High-Dimensional Chaotic Systems with Long Short-Term Memory Networks
Jul 10, 2018
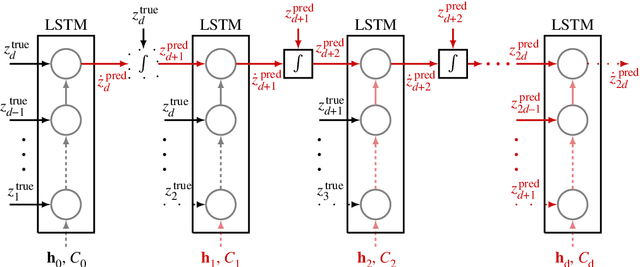


Abstract:We introduce a data-driven forecasting method for high-dimensional chaotic systems using long short-term memory (LSTM) recurrent neural networks. The proposed LSTM neural networks perform inference of high-dimensional dynamical systems in their reduced order space and are shown to be an effective set of nonlinear approximators of their attractor. We demonstrate the forecasting performance of the LSTM and compare it with Gaussian processes (GPs) in time series obtained from the Lorenz 96 system, the Kuramoto-Sivashinsky equation and a prototype climate model. The LSTM networks outperform the GPs in short-term forecasting accuracy in all applications considered. A hybrid architecture, extending the LSTM with a mean stochastic model (MSM-LSTM), is proposed to ensure convergence to the invariant measure. This novel hybrid method is fully data-driven and extends the forecasting capabilities of LSTM networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge