Enhancing Machine Learning Potentials through Transfer Learning across Chemical Elements

Machine Learning Potentials (MLPs) can enable simulations of ab initio accuracy at orders of magnitude lower computational cost. However, their effectiveness hinges on the availability of considerable datasets to ensure robust generalization across chemical space and thermodynamic conditions. The generation of such datasets can be labor-intensive, highlighting the need for innovative methods to train MLPs in data-scarce scenarios. Here, we introduce transfer learning of potential energy surfaces between chemically similar elements. Specifically, we leverage the trained MLP for silicon to initialize and expedite the training of an MLP for germanium. Utilizing classical force field and ab initio datasets, we demonstrate that transfer learning surpasses traditional training from scratch in force prediction, leading to more stable simulations and improved temperature transferability. These advantages become even more pronounced as the training dataset size decreases. The out-of-target property analysis shows that transfer learning leads to beneficial but sometimes adversarial effects. Our findings demonstrate that transfer learning across chemical elements is a promising technique for developing accurate and numerically stable MLPs, particularly in a data-scarce regime.

Learning Non-Local Molecular Interactions via Equivariant Local Representations and Charge Equilibration

Graph Neural Network (GNN) potentials relying on chemical locality offer near-quantum mechanical accuracy at significantly reduced computational costs. By propagating local information to distance particles, Message-passing neural networks (MPNNs) extend the locality concept to model interactions beyond their local neighborhood. Still, this locality precludes modeling long-range effects, such as charge transfer, electrostatic interactions, and dispersion effects, which are critical to adequately describe many real-world systems. In this work, we propose the Charge Equilibration Layer for Long-range Interactions (CELLI) to address the challenging modeling of non-local interactions and the high computational cost of MPNNs. This novel architecture generalizes the fourth-generation high-dimensional neural network (4GHDNN) concept, integrating the charge equilibration (Qeq) method into a model-agnostic building block for modern equivariant GNN potentials. A series of benchmarks show that CELLI can extend the strictly local Allegro architecture to model highly non-local interactions and charge transfer. Our architecture generalizes to diverse datasets and large structures, achieving an accuracy comparable to MPNNs at about twice the computational efficiency.

chemtrain: Learning Deep Potential Models via Automatic Differentiation and Statistical Physics

Neural Networks (NNs) are promising models for refining the accuracy of molecular dynamics, potentially opening up new fields of application. Typically trained bottom-up, atomistic NN potential models can reach first-principle accuracy, while coarse-grained implicit solvent NN potentials surpass classical continuum solvent models. However, overcoming the limitations of costly generation of accurate reference data and data inefficiency of common bottom-up training demands efficient incorporation of data from many sources. This paper introduces the framework chemtrain to learn sophisticated NN potential models through customizable training routines and advanced training algorithms. These routines can combine multiple top-down and bottom-up algorithms, e.g., to incorporate both experimental and simulation data or pre-train potentials with less costly algorithms. chemtrain provides an object-oriented high-level interface to simplify the creation of custom routines. On the lower level, chemtrain relies on JAX to compute gradients and scale the computations to use available resources. We demonstrate the simplicity and importance of combining multiple algorithms in the examples of parametrizing an all-atomistic model of titanium and a coarse-grained implicit solvent model of alanine dipeptide.

Predicting solvation free energies with an implicit solvent machine learning potential

Machine learning (ML) potentials are a powerful tool in molecular modeling, enabling ab initio accuracy for comparably small computational costs. Nevertheless, all-atom simulations employing best-performing graph neural network architectures are still too expensive for applications requiring extensive sampling, such as free energy computations. Implicit solvent models could provide the necessary speed-up due to reduced degrees of freedom and faster dynamics. Here, we introduce a Solvation Free Energy Path Reweighting (ReSolv) framework to parametrize an implicit solvent ML potential for small organic molecules that accurately predicts the hydration free energy, an essential parameter in drug design and pollutant modeling. With a combination of top-down (experimental hydration free energy data) and bottom-up (ab initio data of molecules in a vacuum) learning, ReSolv bypasses the need for intractable ab initio data of molecules in explicit bulk solvent and does not have to resort to less accurate data-generating models. On the FreeSolv dataset, ReSolv achieves a mean absolute error close to average experimental uncertainty, significantly outperforming standard explicit solvent force fields. The presented framework paves the way toward deep molecular models that are more accurate yet computationally cheaper than classical atomistic models.

Accurate machine learning force fields via experimental and simulation data fusion

Machine Learning (ML)-based force fields are attracting ever-increasing interest due to their capacity to span spatiotemporal scales of classical interatomic potentials at quantum-level accuracy. They can be trained based on high-fidelity simulations or experiments, the former being the common case. However, both approaches are impaired by scarce and erroneous data resulting in models that either do not agree with well-known experimental observations or are under-constrained and only reproduce some properties. Here we leverage both Density Functional Theory (DFT) calculations and experimentally measured mechanical properties and lattice parameters to train an ML potential of titanium. We demonstrate that the fused data learning strategy can concurrently satisfy all target objectives, thus resulting in a molecular model of higher accuracy compared to the models trained with a single data source. The inaccuracies of DFT functionals at target experimental properties were corrected, while the investigated off-target properties remained largely unperturbed. Our approach is applicable to any material and can serve as a general strategy to obtain highly accurate ML potentials.

Scalable Bayesian Uncertainty Quantification for Neural Network Potentials: Promise and Pitfalls

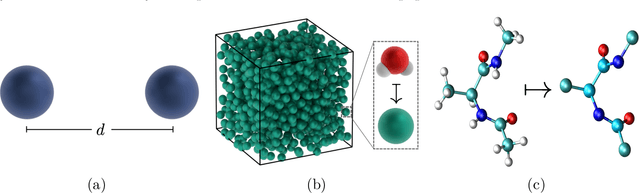
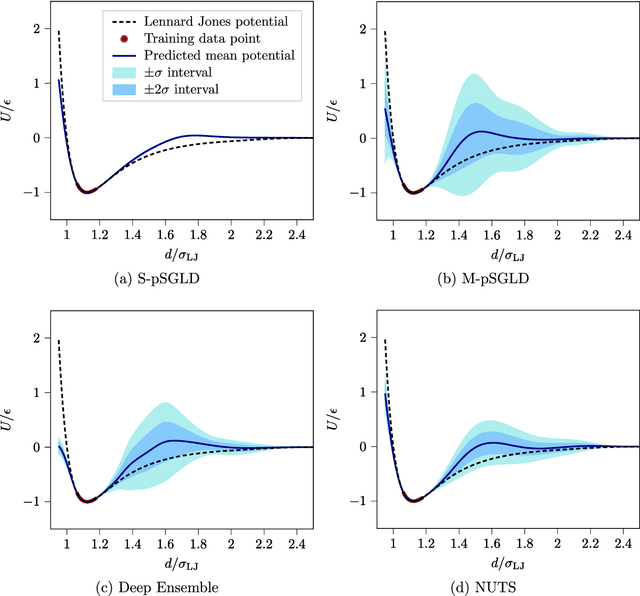
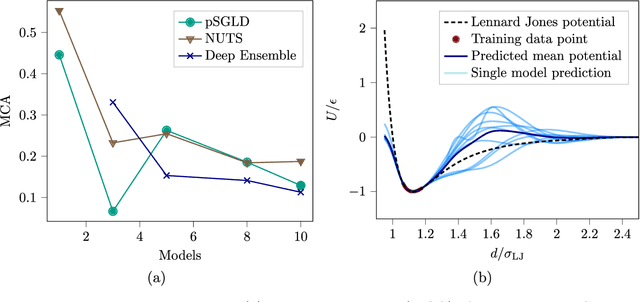
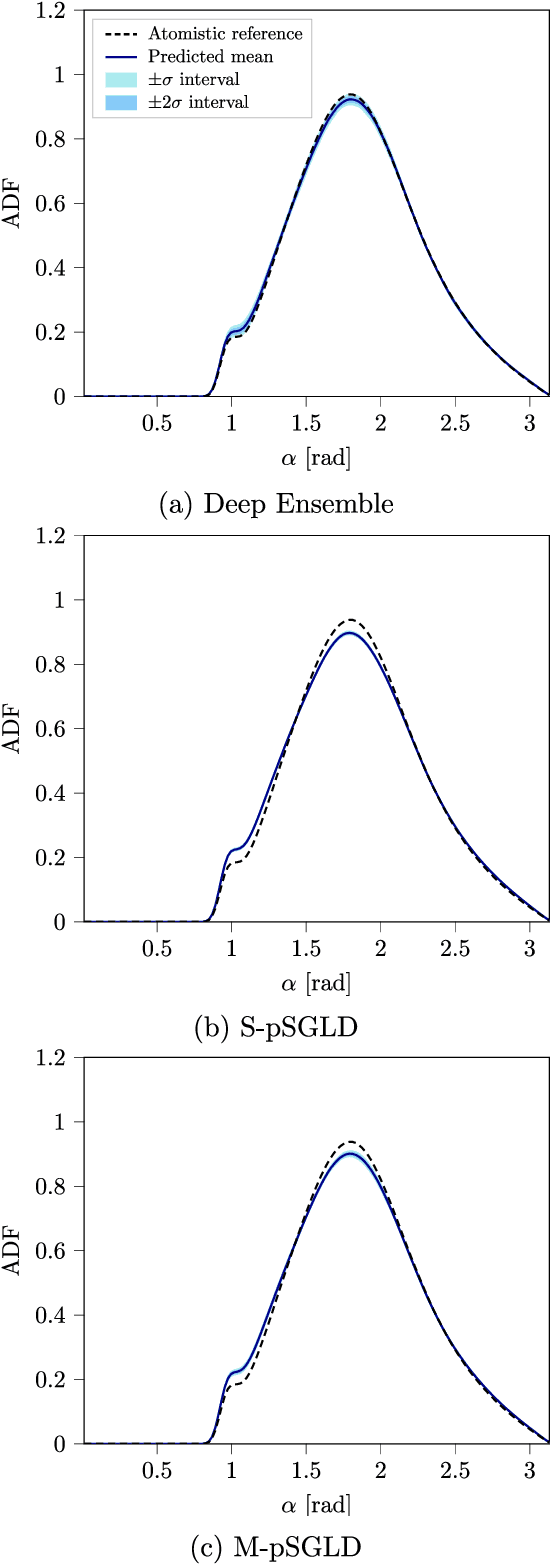
Neural network (NN) potentials promise highly accurate molecular dynamics (MD) simulations within the computational complexity of classical MD force fields. However, when applied outside their training domain, NN potential predictions can be inaccurate, increasing the need for Uncertainty Quantification (UQ). Bayesian modeling provides the mathematical framework for UQ, but classical Bayesian methods based on Markov chain Monte Carlo (MCMC) are computationally intractable for NN potentials. By training graph NN potentials for coarse-grained systems of liquid water and alanine dipeptide, we demonstrate here that scalable Bayesian UQ via stochastic gradient MCMC (SG-MCMC) yields reliable uncertainty estimates for MD observables. We show that cold posteriors can reduce the required training data size and that for reliable UQ, multiple Markov chains are needed. Additionally, we find that SG-MCMC and the Deep Ensemble method achieve comparable results, despite shorter training and less hyperparameter tuning of the latter. We show that both methods can capture aleatoric and epistemic uncertainty reliably, but not systematic uncertainty, which needs to be minimized by adequate modeling to obtain accurate credible intervals for MD observables. Our results represent a step towards accurate UQ that is of vital importance for trustworthy NN potential-based MD simulations required for decision-making in practice.

Learning neural network potentials from experimental data via Differentiable Trajectory Reweighting

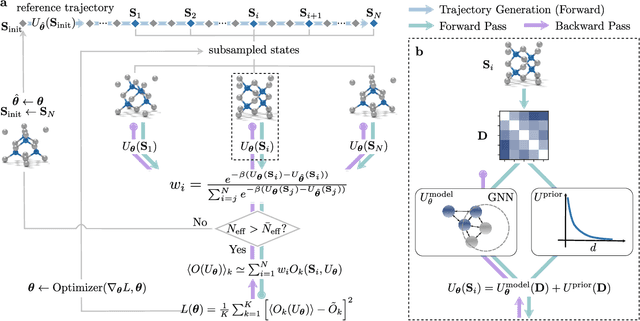
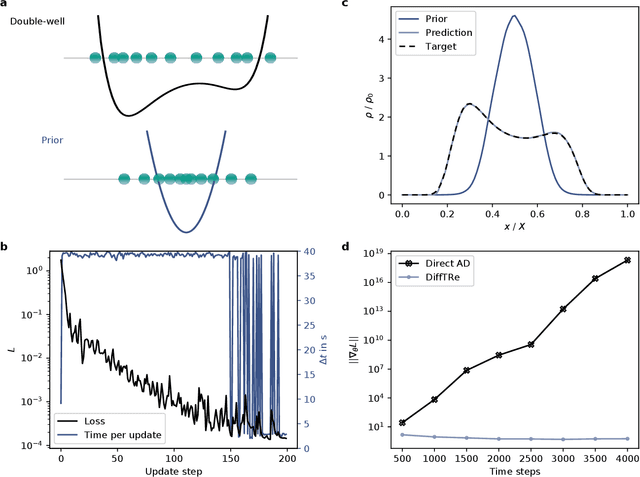
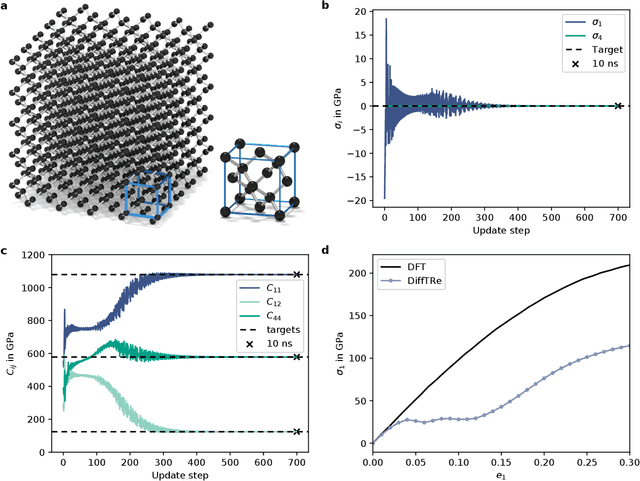
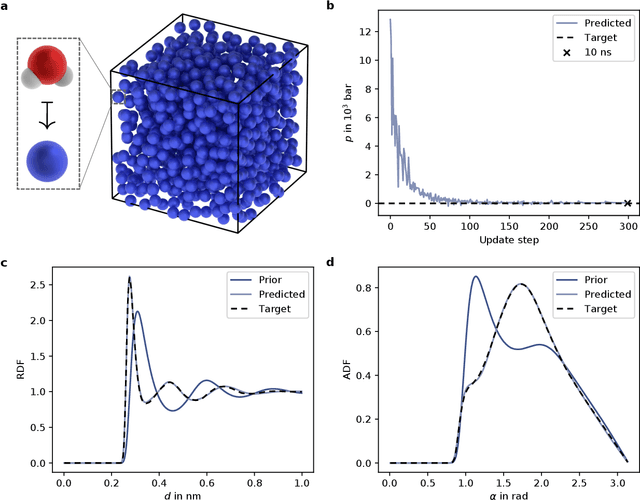
In molecular dynamics (MD), neural network (NN) potentials trained bottom-up on quantum mechanical data have seen tremendous success recently. Top-down approaches that learn NN potentials directly from experimental data have received less attention, typically facing numerical and computational challenges when backpropagating through MD simulations. We present the Differentiable Trajectory Reweighting (DiffTRe) method, which bypasses differentiation through the MD simulation for time-independent observables. Leveraging thermodynamic perturbation theory, we avoid exploding gradients and achieve around 2 orders of magnitude speed-up in gradient computation for top-down learning. We show effectiveness of DiffTRe in learning NN potentials for an atomistic model of diamond and a coarse-grained model of water based on diverse experimental observables including thermodynamic, structural and mechanical properties. Importantly, DiffTRe also generalizes bottom-up structural coarse-graining methods such as iterative Boltzmann inversion to arbitrary potentials. The presented method constitutes an important milestone towards enriching NN potentials with experimental data, particularly when accurate bottom-up data is unavailable.

Accelerated Simulations of Molecular Systems through Learning of their Effective Dynamics

Simulations are vital for understanding and predicting the evolution of complex molecular systems. However, despite advances in algorithms and special purpose hardware, accessing the timescales necessary to capture the structural evolution of bio-molecules remains a daunting task. In this work we present a novel framework to advance simulation timescales by up to three orders of magnitude, by learning the effective dynamics (LED) of molecular systems. LED augments the equation-free methodology by employing a probabilistic mapping between coarse and fine scales using mixture density network (MDN) autoencoders and evolves the non-Markovian latent dynamics using long short-term memory MDNs. We demonstrate the effectiveness of LED in the M\"ueller-Brown potential, the Trp Cage protein, and the alanine dipeptide. LED identifies explainable reduced-order representations and can generate, at any instant, the respective all-atom molecular trajectories. We believe that the proposed framework provides a dramatic increase to simulation capabilities and opens new horizons for the effective modeling of complex molecular systems.