Implicit Delta Learning of High Fidelity Neural Network Potentials

Neural network potentials (NNPs) offer a fast and accurate alternative to ab-initio methods for molecular dynamics (MD) simulations but are hindered by the high cost of training data from high-fidelity Quantum Mechanics (QM) methods. Our work introduces the Implicit Delta Learning (IDLe) method, which reduces the need for high-fidelity QM data by leveraging cheaper semi-empirical QM computations without compromising NNP accuracy or inference cost. IDLe employs an end-to-end multi-task architecture with fidelity-specific heads that decode energies based on a shared latent representation of the input atomistic system. In various settings, IDLe achieves the same accuracy as single high-fidelity baselines while using up to 50x less high-fidelity data. This result could significantly reduce data generation cost and consequently enhance accuracy and generalization, and expand chemical coverage for NNPs, advancing MD simulations for material science and drug discovery. Additionally, we provide a novel set of 11 million semi-empirical QM calculations to support future multi-fidelity NNP modeling.

OpenQDC: Open Quantum Data Commons

Machine Learning Interatomic Potentials (MLIPs) are a highly promising alternative to force-fields for molecular dynamics (MD) simulations, offering precise and rapid energy and force calculations. However, Quantum-Mechanical (QM) datasets, crucial for MLIPs, are fragmented across various repositories, hindering accessibility and model development. We introduce the openQDC package, consolidating 37 QM datasets from over 250 quantum methods and 400 million geometries into a single, accessible resource. These datasets are meticulously preprocessed, and standardized for MLIP training, covering a wide range of chemical elements and interactions relevant in organic chemistry. OpenQDC includes tools for normalization and integration, easily accessible via Python. Experiments with well-known architectures like SchNet, TorchMD-Net, and DimeNet reveal challenges for those architectures and constitute a leaderboard to accelerate benchmarking and guide novel algorithms development. Continuously adding datasets to OpenQDC will democratize QM dataset access, foster more collaboration and innovation, enhance MLIP development, and support their adoption in the MD field.

ET-Flow: Equivariant Flow-Matching for Molecular Conformer Generation

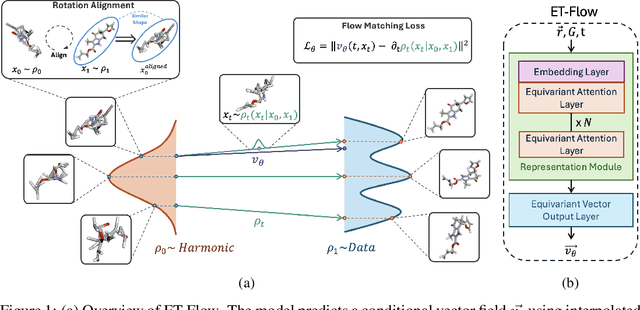
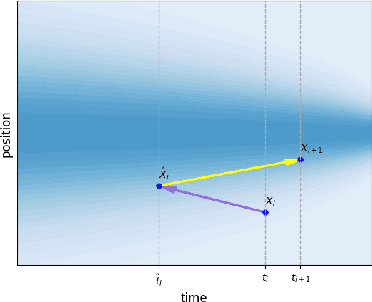
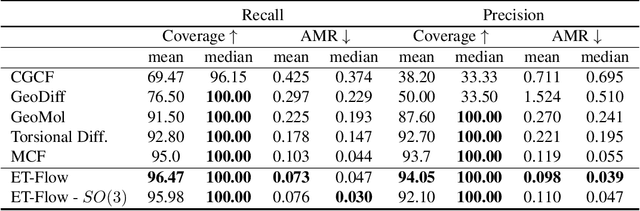
Predicting low-energy molecular conformations given a molecular graph is an important but challenging task in computational drug discovery. Existing state-of-the-art approaches either resort to large scale transformer-based models that diffuse over conformer fields, or use computationally expensive methods to generate initial structures and diffuse over torsion angles. In this work, we introduce Equivariant Transformer Flow (ET-Flow). We showcase that a well-designed flow matching approach with equivariance and harmonic prior alleviates the need for complex internal geometry calculations and large architectures, contrary to the prevailing methods in the field. Our approach results in a straightforward and scalable method that directly operates on all-atom coordinates with minimal assumptions. With the advantages of equivariance and flow matching, ET-Flow significantly increases the precision and physical validity of the generated conformers, while being a lighter model and faster at inference. Code is available https://github.com/shenoynikhil/ETFlow.

chemtrain: Learning Deep Potential Models via Automatic Differentiation and Statistical Physics

Neural Networks (NNs) are promising models for refining the accuracy of molecular dynamics, potentially opening up new fields of application. Typically trained bottom-up, atomistic NN potential models can reach first-principle accuracy, while coarse-grained implicit solvent NN potentials surpass classical continuum solvent models. However, overcoming the limitations of costly generation of accurate reference data and data inefficiency of common bottom-up training demands efficient incorporation of data from many sources. This paper introduces the framework chemtrain to learn sophisticated NN potential models through customizable training routines and advanced training algorithms. These routines can combine multiple top-down and bottom-up algorithms, e.g., to incorporate both experimental and simulation data or pre-train potentials with less costly algorithms. chemtrain provides an object-oriented high-level interface to simplify the creation of custom routines. On the lower level, chemtrain relies on JAX to compute gradients and scale the computations to use available resources. We demonstrate the simplicity and importance of combining multiple algorithms in the examples of parametrizing an all-atomistic model of titanium and a coarse-grained implicit solvent model of alanine dipeptide.

Scalable Bayesian Uncertainty Quantification for Neural Network Potentials: Promise and Pitfalls

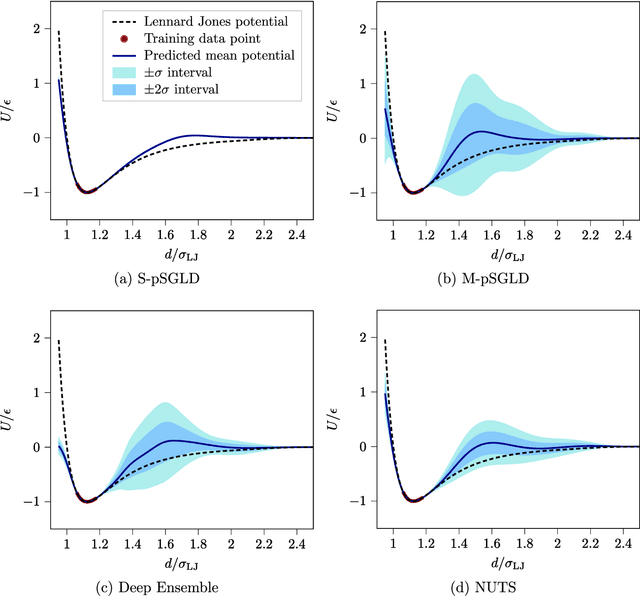
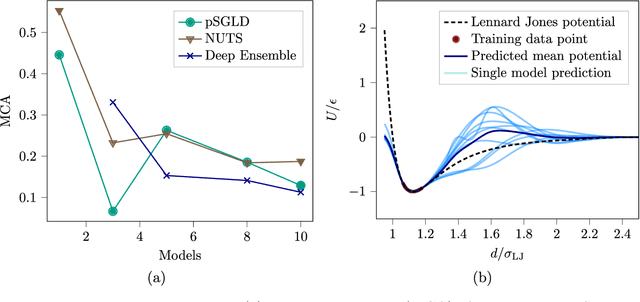
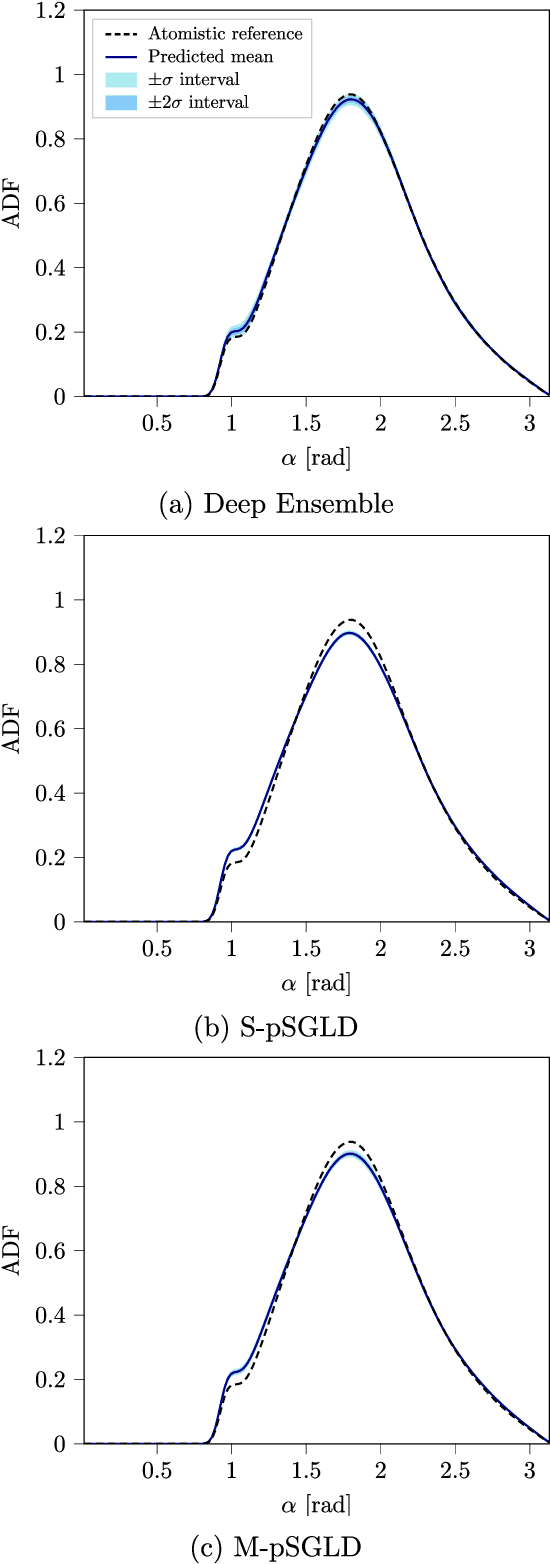
Neural network (NN) potentials promise highly accurate molecular dynamics (MD) simulations within the computational complexity of classical MD force fields. However, when applied outside their training domain, NN potential predictions can be inaccurate, increasing the need for Uncertainty Quantification (UQ). Bayesian modeling provides the mathematical framework for UQ, but classical Bayesian methods based on Markov chain Monte Carlo (MCMC) are computationally intractable for NN potentials. By training graph NN potentials for coarse-grained systems of liquid water and alanine dipeptide, we demonstrate here that scalable Bayesian UQ via stochastic gradient MCMC (SG-MCMC) yields reliable uncertainty estimates for MD observables. We show that cold posteriors can reduce the required training data size and that for reliable UQ, multiple Markov chains are needed. Additionally, we find that SG-MCMC and the Deep Ensemble method achieve comparable results, despite shorter training and less hyperparameter tuning of the latter. We show that both methods can capture aleatoric and epistemic uncertainty reliably, but not systematic uncertainty, which needs to be minimized by adequate modeling to obtain accurate credible intervals for MD observables. Our results represent a step towards accurate UQ that is of vital importance for trustworthy NN potential-based MD simulations required for decision-making in practice.

Learning neural network potentials from experimental data via Differentiable Trajectory Reweighting

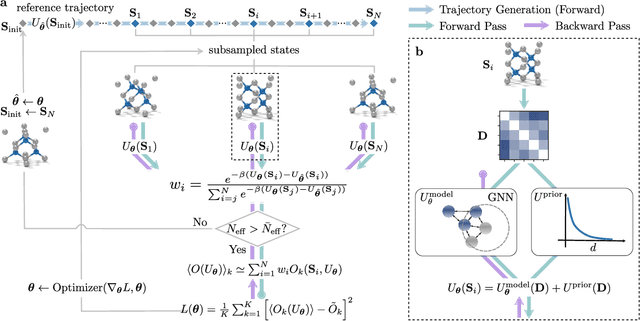
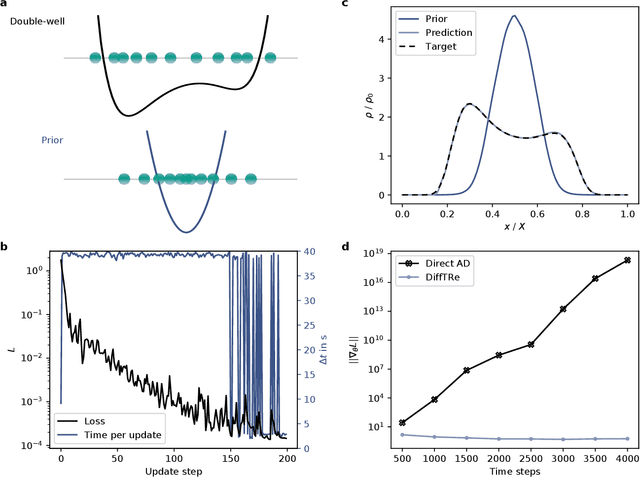
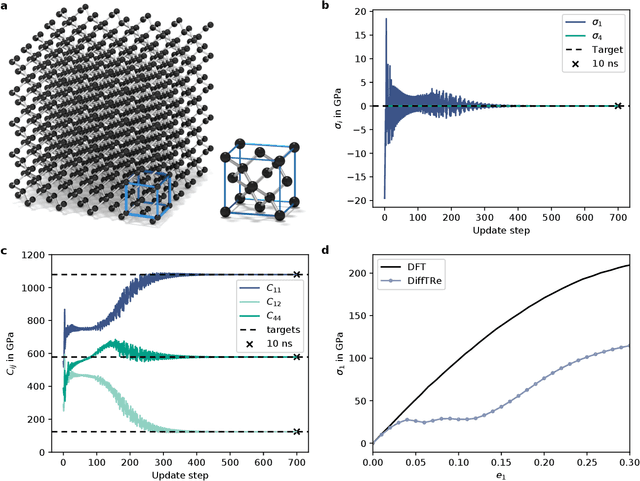
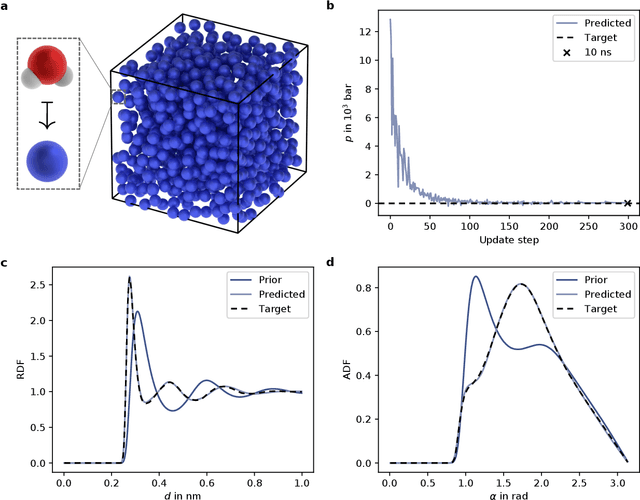
In molecular dynamics (MD), neural network (NN) potentials trained bottom-up on quantum mechanical data have seen tremendous success recently. Top-down approaches that learn NN potentials directly from experimental data have received less attention, typically facing numerical and computational challenges when backpropagating through MD simulations. We present the Differentiable Trajectory Reweighting (DiffTRe) method, which bypasses differentiation through the MD simulation for time-independent observables. Leveraging thermodynamic perturbation theory, we avoid exploding gradients and achieve around 2 orders of magnitude speed-up in gradient computation for top-down learning. We show effectiveness of DiffTRe in learning NN potentials for an atomistic model of diamond and a coarse-grained model of water based on diverse experimental observables including thermodynamic, structural and mechanical properties. Importantly, DiffTRe also generalizes bottom-up structural coarse-graining methods such as iterative Boltzmann inversion to arbitrary potentials. The presented method constitutes an important milestone towards enriching NN potentials with experimental data, particularly when accurate bottom-up data is unavailable.