Can Graph Foundation Models Generalize Over Architecture?

Graph foundation models (GFMs) have recently attracted interest due to the promise of graph neural network (GNN) architectures that generalize zero-shot across graphs of arbitrary scales, feature dimensions, and domains. While existing work has demonstrated this ability empirically across diverse real-world benchmarks, these tasks share a crucial hidden limitation: they admit a narrow set of effective GNN architectures. In particular, current domain-agnostic GFMs rely on fixed architectural backbones, implicitly assuming that a single message-passing regime suffices across tasks. In this paper, we argue that architecture adaptivity is a necessary requirement for true GFMs. We show that existing approaches are non-robust to task-dependent architectural attributes and, as a case study, use range as a minimal and measurable axis along which this limitation becomes explicit. With theoretical analysis and controlled synthetic experiments, we demonstrate that fixed-backbone GFMs provably under-reach on tasks whose architectural requirements differ from those seen at training time. To address this issue, we introduce a framework that adapts effective GNN architecture at inference time by discovering and mixing task-specific linear graph operators, enabling zero-shot generalization across tasks with heterogeneous architectural requirements, without retraining. We validate our approach on arbitrary-range synthetic tasks and a suite of real-world benchmarks, demonstrating improved performance and robustness over existing domain-agnostic GFMs.

MacroGuide: Topological Guidance for Macrocycle Generation

Macrocycles are ring-shaped molecules that offer a promising alternative to small-molecule drugs due to their enhanced selectivity and binding affinity against difficult targets. Despite their chemical value, they remain underexplored in generative modeling, likely owing to their scarcity in public datasets and the challenges of enforcing topological constraints in standard deep generative models. We introduce MacroGuide: Topological Guidance for Macrocycle Generation, a diffusion guidance mechanism that uses Persistent Homology to steer the sampling of pretrained molecular generative models toward the generation of macrocycles, in both unconditional and conditional (protein pocket) settings. At each denoising step, MacroGuide constructs a Vietoris-Rips complex from atomic positions and promotes ring formation by optimizing persistent homology features. Empirically, applying MacroGuide to pretrained diffusion models increases macrocycle generation rates from 1% to 99%, while matching or exceeding state-of-the-art performance on key quality metrics such as chemical validity, diversity, and PoseBusters checks.

Categorical Flow Maps

We introduce Categorical Flow Maps, a flow-matching method for accelerated few-step generation of categorical data via self-distillation. Building on recent variational formulations of flow matching and the broader trend towards accelerated inference in diffusion and flow-based models, we define a flow map towards the simplex that transports probability mass toward a predicted endpoint, yielding a parametrisation that naturally constrains model predictions. Since our trajectories are continuous rather than discrete, Categorical Flow Maps can be trained with existing distillation techniques, as well as a new objective based on endpoint consistency. This continuous formulation also automatically unlocks test-time inference: we can directly reuse existing guidance and reweighting techniques in the categorical setting to steer sampling toward downstream objectives. Empirically, we achieve state-of-the-art few-step results on images, molecular graphs, and text, with strong performance even in single-step generation.

Curly Flow Matching for Learning Non-gradient Field Dynamics

Modeling the transport dynamics of natural processes from population-level observations is a ubiquitous problem in the natural sciences. Such models rely on key assumptions about the underlying process in order to enable faithful learning of governing dynamics that mimic the actual system behavior. The de facto assumption in current approaches relies on the principle of least action that results in gradient field dynamics and leads to trajectories minimizing an energy functional between two probability measures. However, many real-world systems, such as cell cycles in single-cell RNA, are known to exhibit non-gradient, periodic behavior, which fundamentally cannot be captured by current state-of-the-art methods such as flow and bridge matching. In this paper, we introduce Curly Flow Matching (Curly-FM), a novel approach that is capable of learning non-gradient field dynamics by designing and solving a Schr\"odinger bridge problem with a non-zero drift reference process -- in stark contrast to typical zero-drift reference processes -- which is constructed using inferred velocities in addition to population snapshot data. We showcase Curly-FM by solving the trajectory inference problems for single cells, computational fluid dynamics, and ocean currents with approximate velocities. We demonstrate that Curly-FM can learn trajectories that better match both the reference process and population marginals. Curly-FM expands flow matching models beyond the modeling of populations and towards the modeling of known periodic behavior in physical systems. Our code repository is accessible at: https://github.com/kpetrovicc/curly-flow-matching.git

Flock: A Knowledge Graph Foundation Model via Learning on Random Walks

We study the problem of zero-shot link prediction on knowledge graphs (KGs), which requires models to generalize over novel entities and novel relations. Knowledge graph foundation models (KGFMs) address this task by enforcing equivariance over both nodes and relations, learning from structural properties of nodes and relations, which are then transferable to novel graphs with similar structural properties. However, the conventional notion of deterministic equivariance imposes inherent limits on the expressive power of KGFMs, preventing them from distinguishing structurally similar but semantically distinct relations. To overcome this limitation, we introduce probabilistic node-relation equivariance, which preserves equivariance in distribution while incorporating a principled randomization to break symmetries during inference. Building on this principle, we present Flock, a KGFM that iteratively samples random walks, encodes them into sequences via a recording protocol, embeds them with a sequence model, and aggregates representations of nodes and relations via learned pooling. Crucially, Flock respects probabilistic node-relation equivariance and is a universal approximator for isomorphism-invariant link-level functions over KGs. Empirically, Flock perfectly solves our new diagnostic dataset Petals where current KGFMs fail, and achieves state-of-the-art performances on entity- and relation prediction tasks on 54 KGs from diverse domains.

Flow-Based Fragment Identification via Binding Site-Specific Latent Representations

Fragment-based drug design is a promising strategy leveraging the binding of small chemical moieties that can efficiently guide drug discovery. The initial step of fragment identification remains challenging, as fragments often bind weakly and non-specifically. We developed a protein-fragment encoder that relies on a contrastive learning approach to map both molecular fragments and protein surfaces in a shared latent space. The encoder captures interaction-relevant features and allows to perform virtual screening as well as generative design with our new method LatentFrag. In LatentFrag, fragment embeddings and positions are generated conditioned on the protein surface while being chemically realistic by construction. Our expressive fragment and protein representations allow location of protein-fragment interaction sites with high sensitivity and we observe state-of-the-art fragment recovery rates when sampling from the learned distribution of latent fragment embeddings. Our generative method outperforms common methods such as virtual screening at a fraction of its computational cost providing a valuable starting point for fragment hit discovery. We further show the practical utility of LatentFrag and extend the workflow to full ligand design tasks. Together, these approaches contribute to advancing fragment identification and provide valuable tools for fragment-based drug discovery.

Of Graphs and Tables: Zero-Shot Node Classification with Tabular Foundation Models

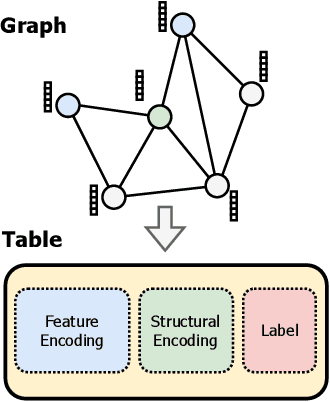
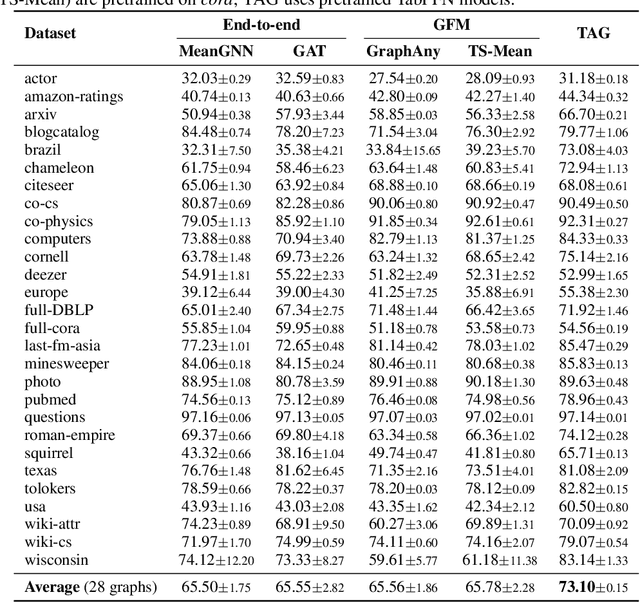
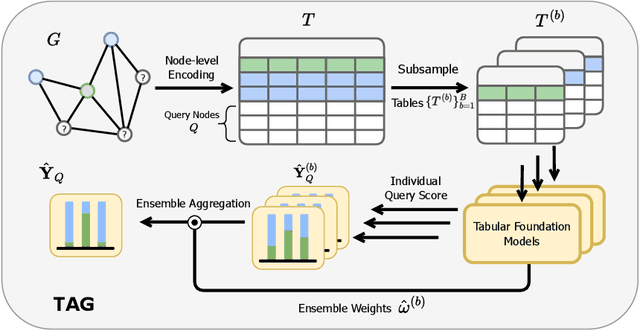
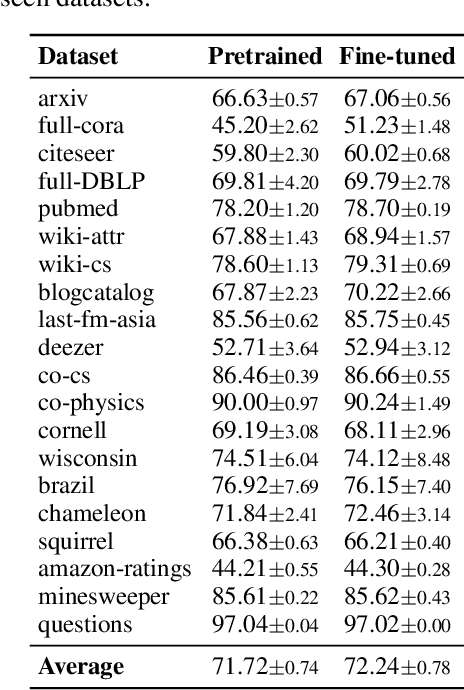
Graph foundation models (GFMs) have recently emerged as a promising paradigm for achieving broad generalization across various graph data. However, existing GFMs are often trained on datasets that were shown to poorly represent real-world graphs, limiting their generalization performance. In contrast, tabular foundation models (TFMs) not only excel at classical tabular prediction tasks but have also shown strong applicability in other domains such as time series forecasting, natural language processing, and computer vision. Motivated by this, we take an alternative view to the standard perspective of GFMs and reformulate node classification as a tabular problem. Each node can be represented as a row with feature, structure, and label information as columns, enabling TFMs to directly perform zero-shot node classification via in-context learning. In this work, we introduce TabGFM, a graph foundation model framework that first converts a graph into a table via feature and structural encoders, applies multiple TFMs to diversely subsampled tables, and then aggregates their outputs through ensemble selection. Through experiments on 28 real-world datasets, TabGFM achieves consistent improvements over task-specific GNNs and state-of-the-art GFMs, highlighting the potential of tabular reformulation for scalable and generalizable graph learning.

Multi-domain Distribution Learning for De Novo Drug Design

We introduce DrugFlow, a generative model for structure-based drug design that integrates continuous flow matching with discrete Markov bridges, demonstrating state-of-the-art performance in learning chemical, geometric, and physical aspects of three-dimensional protein-ligand data. We endow DrugFlow with an uncertainty estimate that is able to detect out-of-distribution samples. To further enhance the sampling process towards distribution regions with desirable metric values, we propose a joint preference alignment scheme applicable to both flow matching and Markov bridge frameworks. Furthermore, we extend our model to also explore the conformational landscape of the protein by jointly sampling side chain angles and molecules.

GradMetaNet: An Equivariant Architecture for Learning on Gradients

Gradients of neural networks encode valuable information for optimization, editing, and analysis of models. Therefore, practitioners often treat gradients as inputs to task-specific algorithms, e.g. for pruning or optimization. Recent works explore learning algorithms that operate directly on gradients but use architectures that are not specifically designed for gradient processing, limiting their applicability. In this paper, we present a principled approach for designing architectures that process gradients. Our approach is guided by three principles: (1) equivariant design that preserves neuron permutation symmetries, (2) processing sets of gradients across multiple data points to capture curvature information, and (3) efficient gradient representation through rank-1 decomposition. Based on these principles, we introduce GradMetaNet, a novel architecture for learning on gradients, constructed from simple equivariant blocks. We prove universality results for GradMetaNet, and show that previous approaches cannot approximate natural gradient-based functions that GradMetaNet can. We then demonstrate GradMetaNet's effectiveness on a diverse set of gradient-based tasks on MLPs and transformers, such as learned optimization, INR editing, and estimating loss landscape curvature.

Equivariance Everywhere All At Once: A Recipe for Graph Foundation Models

Graph machine learning architectures are typically tailored to specific tasks on specific datasets, which hinders their broader applicability. This has led to a new quest in graph machine learning: how to build graph foundation models capable of generalizing across arbitrary graphs and features? In this work, we present a recipe for designing graph foundation models for node-level tasks from first principles. The key ingredient underpinning our study is a systematic investigation of the symmetries that a graph foundation model must respect. In a nutshell, we argue that label permutation-equivariance alongside feature permutation-invariance are necessary in addition to the common node permutation-equivariance on each local neighborhood of the graph. To this end, we first characterize the space of linear transformations that are equivariant to permutations of nodes and labels, and invariant to permutations of features. We then prove that the resulting network is a universal approximator on multisets that respect the aforementioned symmetries. Our recipe uses such layers on the multiset of features induced by the local neighborhood of the graph to obtain a class of graph foundation models for node property prediction. We validate our approach through extensive experiments on 29 real-world node classification datasets, demonstrating both strong zero-shot empirical performance and consistent improvement as the number of training graphs increases.